step
动态系统的阶跃响应
语法
说明
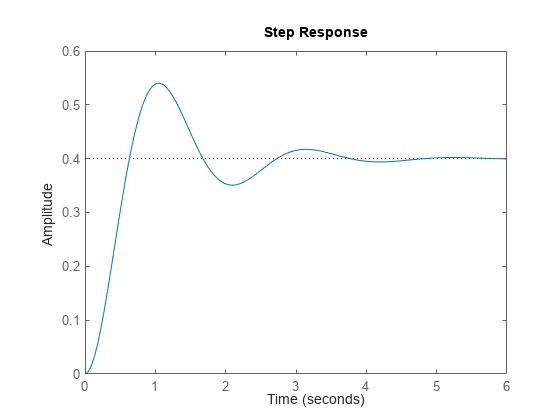
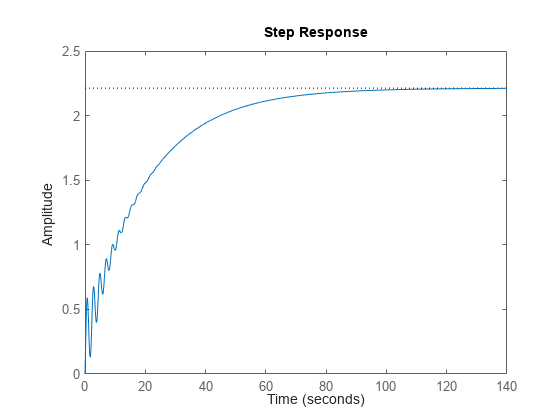
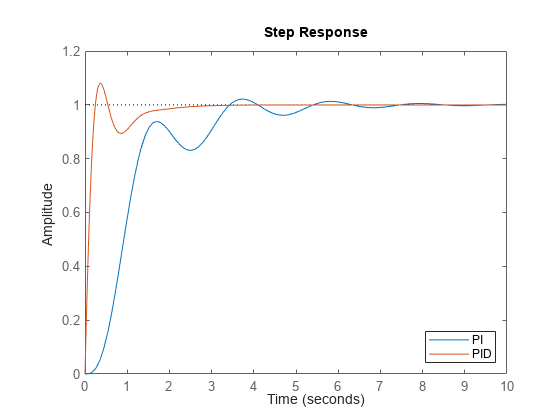
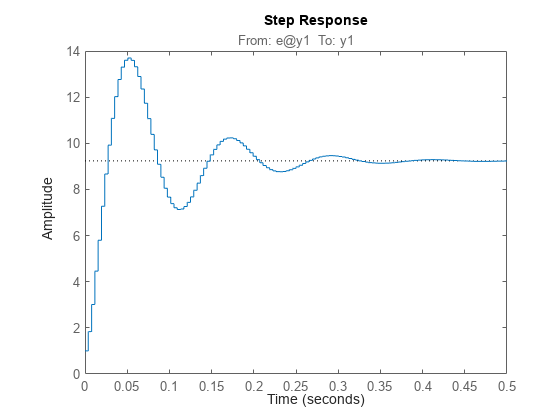
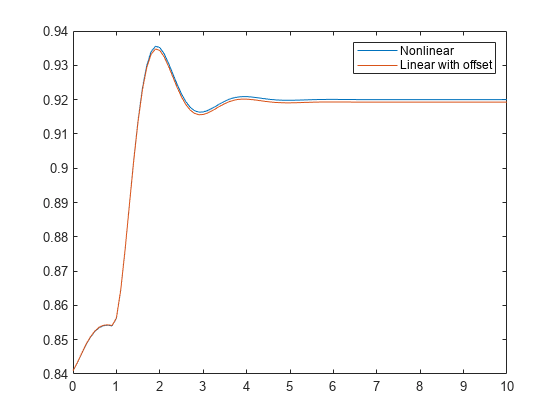
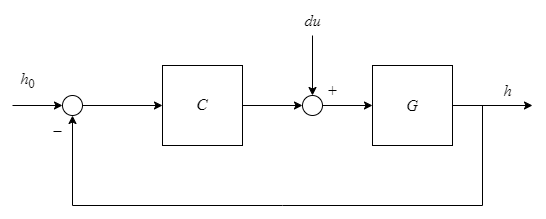
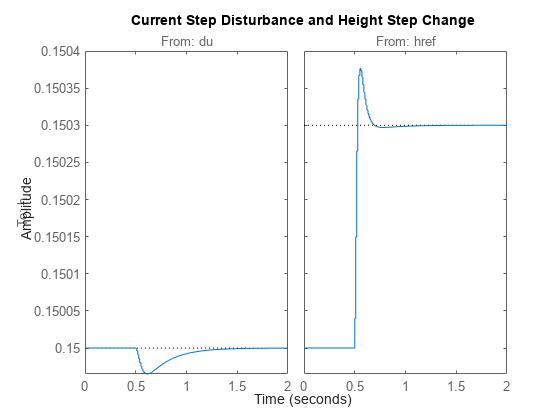
step 计算经过 td 个时间单位后,系统对于输入值从 U 阶跃变化到 U + dU 的阶跃响应。
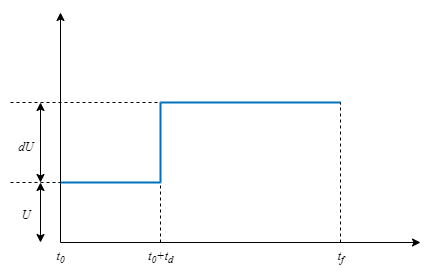
其中,
t0 是仿真开始时间。
td 是阶跃延迟。
U 是基线输入值或偏置。
dU 是阶跃振幅。
默认情况下,该函数对 t0 = 0、U = 0、dU = 1 和 td = 0 应用阶跃。但是,您可以使用 RespConfig 配置这些值。您还可以指定初始状态 x (t0)。如果您未指定初始状态,step 会假定系统最初处于静止状态,输入电平为 U。
[ 指定用于计算阶跃响应的其他选项,例如阶跃振幅或输入偏移量。使用 y,tOut] = step(___,config)RespConfig 创建 config。
示例
输入参数
输出参量
提示
算法
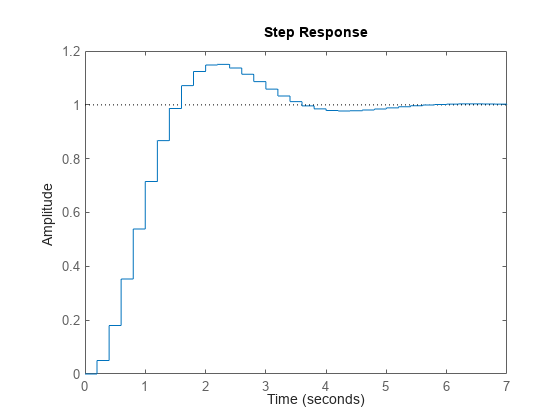
为了获得没有内部延迟的连续时间模型的样本,step 将此类模型转换为状态空间模型,并通过对输入使用零阶保持使这些模型离散化。step 根据系统动态特性自动选择此离散化的采样时间,除非您以 t = T0:dt:Tf 形式提供输入时间向量 t。在这种情况下,step 使用 dt 作为采样时间。生成的仿真时间步 tOut 是以间隔 dt 等间隔采样的。
对于具有内部延迟的系统,Control System Toolbox™ 软件使用变步长求解器。因此,时间步 tOut 不是等间隔采样的。
参考
[1] L.F. Shampine and P. Gahinet, "Delay-differential-algebraic equations in control theory," Applied Numerical Mathematics, Vol. 56, Issues 3–4, pp. 574–588.