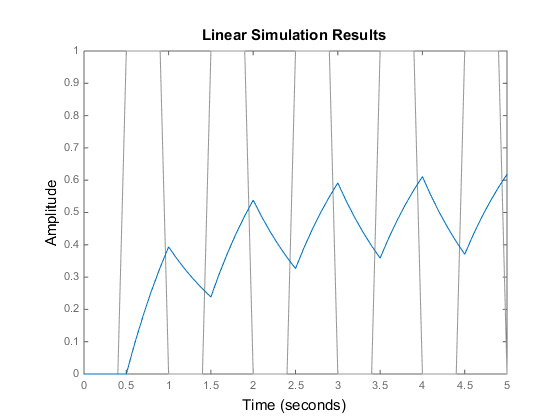
lsim
计算动态系统对任意输入的时间响应仿真数据
语法
说明
响应数据
输入插值方法
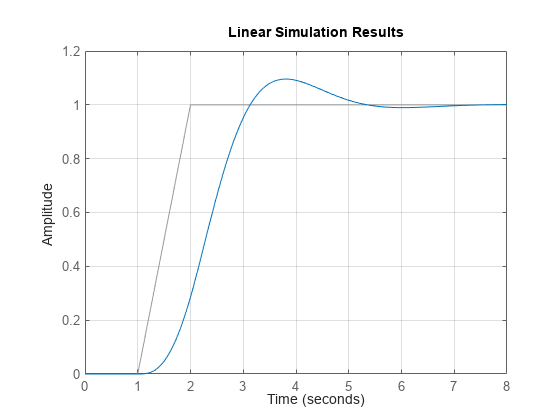
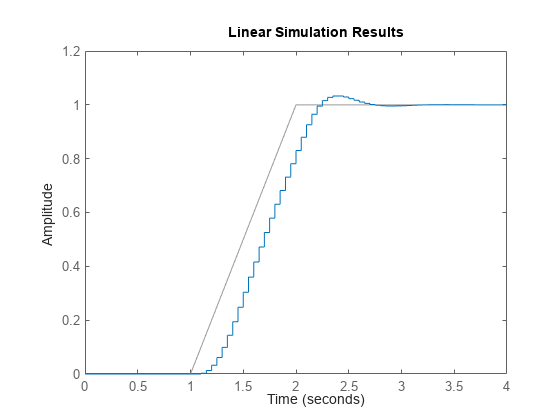
当 sys 是连续时间模型时,[___] = lsim(___, 指定 method)lsim 如何在采样之间对输入值进行插值。
状态快照 POD
自 R2024b 起
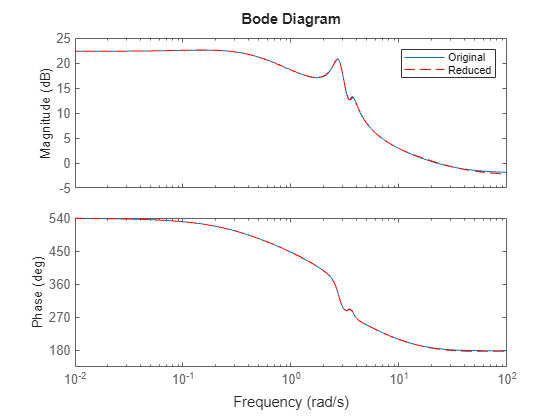
[ 对 LTI 状态空间模型 y,tOut,x,~,xPODOut] = lsim(___,xPODIn)sys 的状态快照执行本征正交分解 (POD)。这里,xPOD 是一个 incrementalPOD 对象。您可以开始新的 POD 分析或向先前的 POD 结果中添加数据。有关示例和模型降阶应用,请参阅 incrementalPOD (Control System Toolbox) 和 reducespec (Control System Toolbox)。
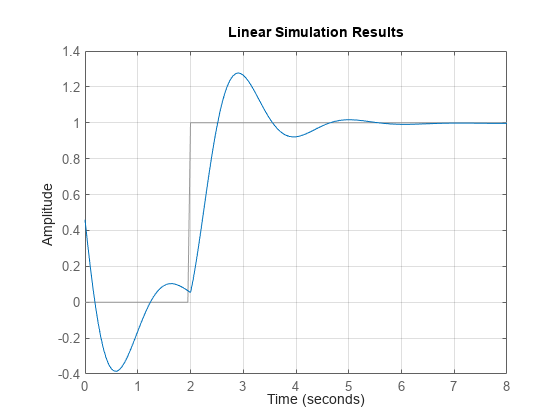
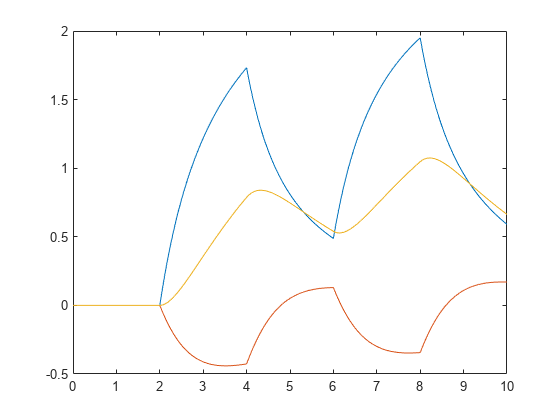
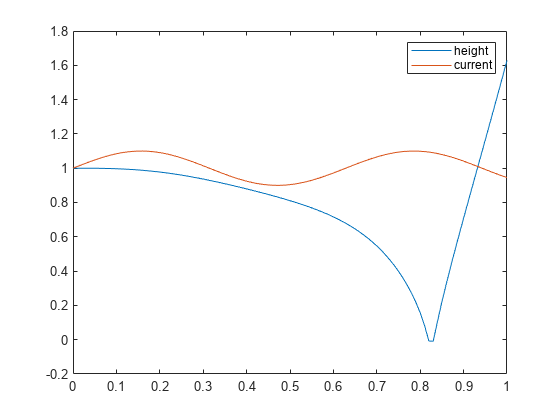
响应图
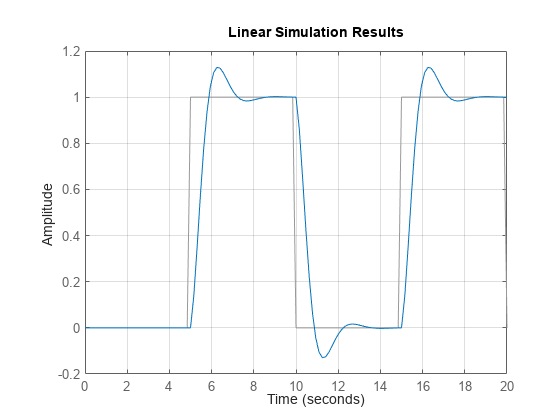
lsim(___) 绘制 sys 对所有先前输入参量组合(除状态快照 POD 外)的输入历史记录 (u,t) 的仿真时间响应图。该图使用默认的绘图选项。如需更多绘图自定义选项,请改用 lsimplot。
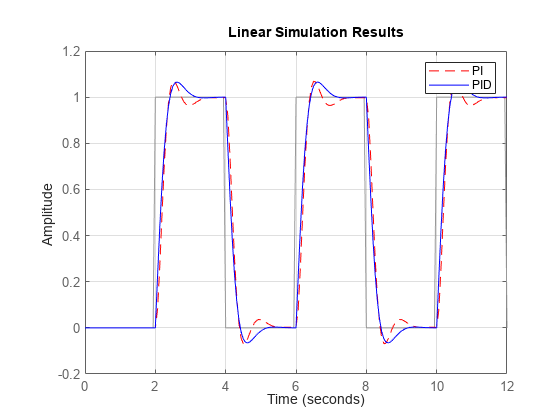
要在同一图上绘制多个动态系统的响应,您可以将
sys指定为以逗号分隔的模型列表。例如,lsim(sys1,sys2,sys3,u,t)在同一图上绘制三个模型的响应。要为图中的每个系统分别指定一种颜色、线型和标记,请为每个系统指定
LineSpec值。例如,lsim(sys1,LineSpec1,sys2,LineSpec2,u,t)绘制两个模型并指定它们的绘图样式。有关指定LineSpec值的详细信息,请参阅lsimplot。
示例
输入参数
输出参量
提示
当您需要额外的绘图自定义选项时,请改用
lsimplot。使用
lsim创建的绘图不支持以字符串数组或字符向量元胞数组形式指定的多行标题或标签。要指定多行标题和标签,请使用包含newline字符的单个字符串。lsim(sys,u,t) title("first line" + newline + "second line");
算法
对于离散时间传递函数,
lsim 根据与此传递函数相关的递归对输入进行滤波:
对于离散时间 zpk 模型,lsim 通过一系列一阶或二阶节对输入进行滤波。这种方法避免了形成分子和分母多项式,因为对于高阶模型来说,形成这些多项式可能会导致数值不稳定。
对于离散时间状态空间模型,lsim 传播离散时间状态空间方程,
对于连续时间系统,lsim 首先使用 c2d 对系统进行离散化,然后传播得到的离散时间状态空间方程。除非您使用 method 输入参量另行指定,否则 lsim 在输入信号平滑时使用一阶保持离散化方法,而在输入信号不连续(例如脉冲或方波)时使用零阶保持离散化方法。离散化的采样时间是您在 t 中提供的时间采样之间的间隔 dT。
对于连续时间稀疏模型、LTV 模型和 LPV 模型,lsim 使用基于 trbdf 或 hht 方法的定步长求解器(请参阅 sparss 和 mechss 模型的 SolverOptions 属性)。