基于自编码器的神经状态空间模型对非线性动力系统进行降阶建模

此示例使用:

本示例展示了利用神经状态空间 (NSS) 建模技术对非线性动力学系统进行降阶建模的过程。用于描述该方法的非线性系统是由多个非线性质量-弹簧-阻尼 (MSD) 系统级联而成的。降阶模型的开发关键在于训练包含三个部分的神经网络：

将数据映射到低维空间的编码器网络
在编码空间中学习动力学的状态网络
将数据映射回原始空间的解码器网络

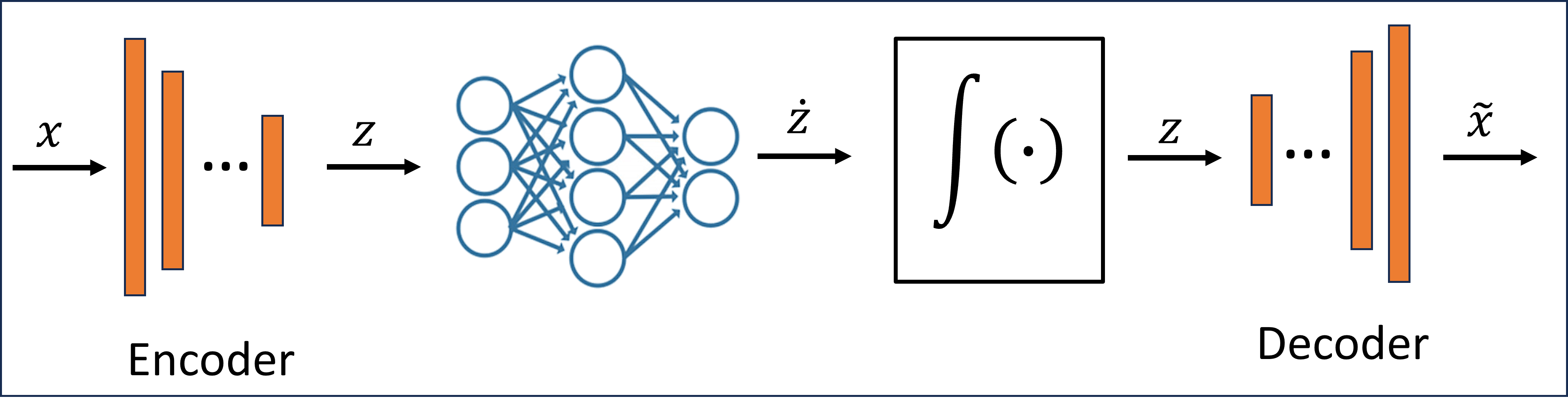
用于收集数据的 Simulink® 模型已在Reduced Order Modeling of a Nonlinear Dynamical System as an Identified Linear Parameter Varying Model示例中介绍。

你选取 25 个质点，由此形成一个 50 维的维度，其中前 25 个状态 $x$ 表示每个质点的位置，后 25 个状态 $x_{}^{˙}$ 表示每个质点的速度。非线性体现在每个弹簧的刚度 $k (x) = k_{1} x + k_{2} x^{3}$ 中。在无外部扰动 ( $F = 0$ ) 的情况下激励系统，并施加随机阶梯输入 $u$ 。你收集所有状态，包括位置 $x$ 和速度 $x_{}^{˙}$ ，并将这个组合状态向量作为输出 $y$ 。目标是确定一种神经状态空间模型，该模型采用自编码器有效地封装这些非线性动力学特性。

数据准备

设置仿真 MSD 系统所需参数的值。您需设定质量数 $M = 25$ 、单个模块的质量 $m = 1 kg$ 、线性弹簧刚度 $k_{1} = 0.5 N / m$ 、三次弹簧刚度 $k_{2} = 1$ ${N / m}^{3}$ 、线性阻尼系数 $b_{1} = 1 N / (m / s)$ 以及三次阻尼系数 $b_{2} = 0.1 N / {(m / s)}^{3}$ 。

rng default
M = 25;
m = 1;
k1 = 0.5;
k2 = 1;
b1 = 1;
b2 = 0.1;

实验设置

使用示例末尾定义的辅助函数 stairInputs 生成两个随机的阶梯式输入。你用第一个来训练模型，第二个用于验证。

Nt = 1000;   % number of samples
Nu = 2;      % number of input sequences
for i = 1:Nu
   [u{i},tin] = stairInputs(Nt);
end

所有质点在起初都是静止的。你通过输入信号激发它们，从而启动振荡。

ic = zeros(2*M,1);  
Tf = tin(end);
dt = tin(2) - tin(1);

% Initial condition for Simulink model (needed to update the size of x in MSD_NL)
F = 0;
U0 = 0;
dFt = [0, 0; Tf, 0];

通过仿真 Simulink 模型收集数据。

dXall = zeros(2*M,Nt,Nu);
dUall = zeros(1,Nt,Nu);

for i=1:Nu
   x0 = ic;
   uin = u{i};
   dut = [tin(:) uin(:)];
   simout_NL = sim('MSD_NL');
   states = simout_NL.simout.Data;
   states = squeeze(states);

   dXall(:,:,i) = states;
   dUall(:,:,i) = uin;
end

X = permute(dXall,[2,1,3]);
U = permute(dUall,[2,1,3]);
X = squeeze(mat2cell(X,Nt,2*M,ones(1,Nu)));
U = squeeze(mat2cell(U,Nt,1,ones(1,Nu)));

zt = iddata(X{1}, U{1}, Ts=dt, Tstart=0); % training data

zv = iddata(X{2}, U{2}, Ts=dt, Tstart=0); % validation data

数据显示

显示输入数据以及估计和验证数据的 $i^{th}$ 状态。

i =25;
z_training = zt;
z_training.y = z_training.y(:,i);
z_validation = zv;
z_validation.y = z_validation.y(:,i);
idplot(z_training,z_validation)
legend

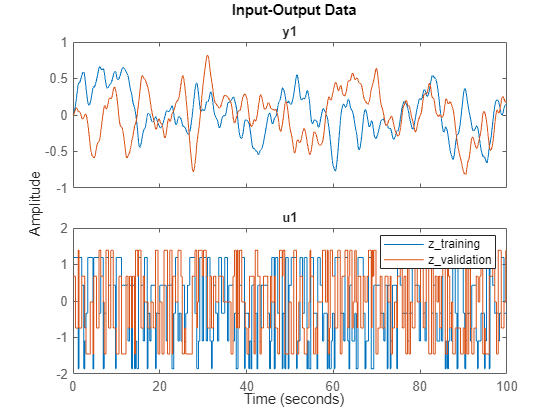
Figure contains 2 axes objects. Axes object 1 with title y1 contains 2 objects of type line. These objects represent untitled1, untitled2. Axes object 2 with title u1 contains 2 objects of type line. These objects represent untitled1, untitled2.

通过操作旋转器，你会发现当 i 取值为 1 至 20 且 i 取值为 26 至 45 时，状态值非常小。这符合物理定律，因为这些状态代表最左侧的质点，它们几乎不受最右侧质点所受力的影响。这也表明，只有最右侧的五个质量体携带了大部分能量。因此选择将模型阶数降至 10（五个组件各取两个状态）。

NSS 模型估计

首先创建 NSS 对象及其用于训练的状态网络、编码器网络和解码器网络。将 idNeuralStateSpace 对象的LatentDim属性设置为 10，因为您正在将模型阶数降低至 10。

rng default
nx = 50;
nu = 1;
nd = 10;
nss = idNeuralStateSpace(nx,NumInputs=nu,LatentDim=nd);
nss.StateNetwork = createMLPNetwork(nss,'state',...
   LayerSizes=[128 128],Activations="tanh");
nss.Encoder = createMLPNetwork(nss,'encoder',...
   LayerSizes=[128 128], Activations="tanh");
nss.Decoder = createMLPNetwork(nss,'decoder',...
   LayerSizes=[128 128],Activations="tanh");

使用nssTrainingOptions指定训练选项。

opt = nssTrainingOptions('adam');
opt.LearnRate = 0.0015;
opt.MaxEpochs = 100;
opt.MiniBatchSize = 800;
opt.WindowSize = 40;
opt.Overlap = 39;

使用 nlssest 训练模型。

warnState = warning('off','Ident:estimation:NparGTNsamp');
cleanupObj = onCleanup(@()warning(warnState));
sys = nlssest(zt,nss,opt);

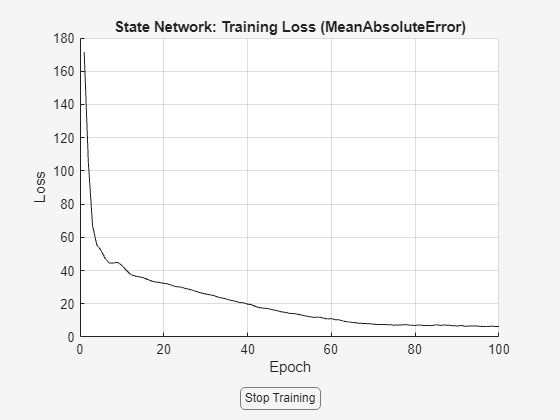
Figure Loss contains an axes object and another object of type uigridlayout. The axes object with title State Network: Training Loss (MeanAbsoluteError), xlabel Epoch, ylabel Loss contains an object of type animatedline.

Generating estimation report...done.

clear("cleanupObj");

NSS 模型验证

验证模型，并计算验证数据与仿真输出之间的均方误差。

zy = sim(sys,zv);
MSE = goodnessOfFit(zv.y,zy.y,'MSE')

MSE = 
0.0037

显示 $j^{th}$ 状态的验证数据和仿真结果。

j = 25;
zref = zv;    % validation data
zref.y = zref.y(:,j);
zsim = zy;    % simulation result
zsim.Name = '';
zsim.y = zsim.y(:,j);   
idplot(zref,zsim)
legend

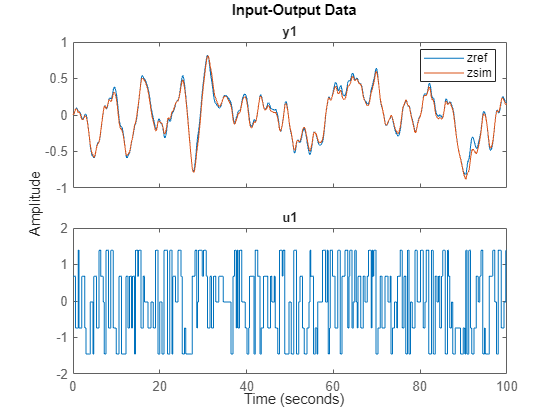
Figure contains 2 axes objects. Axes object 1 with title y1 contains 2 objects of type line. These objects represent untitled1, untitled2. Axes object 2 with title u1 contains an object of type line. This object represents untitled1.

mdl = 'MSD_NSS';
open_system(mdl)
sim(mdl);

请注意，左侧 20 个质量的仿真结果不理想，因为这些值过小，在估计阶段被忽略了。要了解这些状态的动态特性，可通过增加编码器的潜在维度和/或对训练数据进行归一化处理（使每个状态对应的误差获得同等重视）。

生成随机阶梯信号函数

function [stairSignal, t] = stairInputs(L)
stepHeights = randi([1, 5], 1, L); % Random step heights between 1 and 5

rng default 
stepWidths = randi([2, 6], 1, L); % Random step widths between 2 and 6

stairSignal = repelem(stepHeights, stepWidths);
stairSignal = normalize(stairSignal);
stairSignal = stairSignal(1:L);
t = 0:(length(stairSignal) - 1);
t = t/10;
end

另请参阅

对象

idNeuralStateSpace | iddata

函数

createMLPNetwork | nssTrainingOptions | nlssest | sim | idplot | goodnessOfFit