什么是神经状态空间建模?
神经状态空间模型是一种非线性状态空间模型,其中使用神经网络来建模定义系统的状态转换函数和测量函数。您可以使用 System Identification Toolbox™ 软件识别这些网络的权重和偏置。您可以在命令行、System IdentificationApp 或 Simulink® 中使用训练好的模型进行仿真和预测模型输出。您还可以将训练好的模型用于控制、估计、优化和降阶建模。
神经状态空间模型的建模结构
状态空间模型是通过状态方程和输出方程来描述动态系统的建模方法。
状态方程是一组一阶常微分方程 (ODEs) 或差分方程,通常基于第一性原理推导得出(白盒建模)。然而在实践中,由于缺乏先验知识或系统固有的复杂非线性动力学特性,要找到能精确描述系统的解析方程并非易事。
在这些情况下,数据驱动建模(灰箱或黑盒建模)可成为一种有效的替代方案。其中一种数据驱动的方法是神经状态空间建模,它通过神经网络同时表示非线性系统的状态方程和输出方程。
连续时间神经状态空间模型具有如下通用形式,包含状态方程与输出方程:
其中状态函数 F 与非平凡输出函数 H 均由神经网络近似实现。此处,x、u 和 y 分别是表示系统状态、输入和测量输出的向量。t 表示独立变量时间。
当状态不可测量时,为实现状态函数的训练,将测量输出作为状态使用。因此,你将输出 y 固定为等于状态 x。若状态可测量,则将状态固定为输出前缀 y1,并将后缀 y2 固定为测量结果,随后将其与前缀拼接形成最终输出 y。在此,e1 和 e2 是数据集中的测量噪声,通过网络训练算法得以最小化。
对于离散时间状态空间系统,状态方程与输出方程具有如下形式:
其中 x(t+1) 表示下一个采样时点的被控对象状态。
神经状态空间模型的定义与建模
估计神经状态空间模型需要测量系统的状态。如果它们未被测量,则可将输出视为状态。
要创建具有可识别的网络权重和偏置的连续时间或离散时间神经状态空间黑盒模型,请使用 idNeuralStateSpace。您可以通过将多层感知器网络或自定义网络指定为状态或输出函数网络,来更改模型的默认状态和输出网络。
多层感知器网络 (MLP) 属于前馈人工神经网络 (ANN) 的一类。多层感知器 (MLP) 至少包含三层节点:输入层、一个或多个隐藏层以及输出层。自定义网络指的是任何可通过 dlnetwork (Deep Learning Toolbox) 创建的神经网络结构。
多层感知器网络具有固定结构,使用起来非常简单。该网络的训练通常更快。另一方面,自定义网络允许采用先进的网络结构设计,从而提升性能。有关示例,请参阅利用灵活的非线性函数增强已知线性模型。在创建自定义网络时,您还可灵活使用 Deep Learning Toolbox™ 的某些高级层,例如 dropoutLayer 和 batchNormalizationLayer。
具有至少一个隐藏层且采用压制函数(如双曲正切或 sigmoid 函数)的多层感知器 (MLP) 网络是通用逼近器,即在隐藏单元数量充足的情况下,理论上能够以任意所需精度逼近任意函数。更深的网络(具有更多隐藏层的网络)能够像浅层网络一样近似组合函数,但其训练参数数量和样本复杂度却呈指数级下降。
要将多层感知器 (MLP) 网络指定为状态或输出函数网络,请使用 createMLPNetwork。要分配自定义网络,请直接将 dlnetwork 对象作为状态或输出函数进行分配,或使用 setNetwork。
要使用测得的时间域系统数据训练神经状态空间模型,请使用 nlssest,该工具可更新网络的权重和偏置。您可以使用 Adam、SGDM、RMSProp 或 L-BFGS 求解器对模型进行训练。有关这些算法的更多信息,请参阅trainingOptions (Deep Learning Toolbox)的算法章节。
新的训练从先前训练过的网络开始。要重置网络,您可以手动分配 dlnetwork 对象的学习参数,或对其进行初始化。
神经状态空间模型中的自编码器
在神经状态空间模型中使用自编码器,将模型状态映射到与原始状态空间维度不同的 latent 空间。这样做使您能够将状态投影到低维空间,从而实现降阶建模应用。您还可以选择比原始维度更大的潜在空间维度,这有助于在潜在空间中将状态转移函数线性化。
离散时间状态空间系统包含状态网络和输出网络。
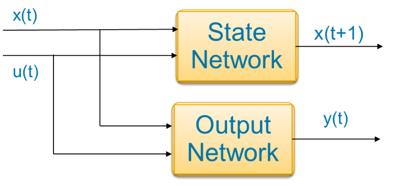
要使用自编码器,需要添加一个对输入数据进行转换的编码器网络和一个重建输入数据的解码器网络。为此,请将 idNeuralStateSpace 对象的 LatentDim 属性指定为有限的正整数。
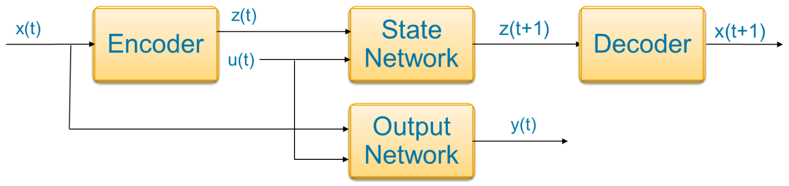
此处,x(t) 为状态测量值,u(t) 为输入,y(t) 为测量输出,z(t) 为时间点 t 的潜在状态。图中所示的四个网络是:
Encoder - x(t) 是编码器的输入,通常由高维数据构成。潜在状态 z(t) 是编码器的输出。这相对低维,且能捕捉数据的主要特征。编码器将 x(t) 映射到 z(t)。
State Network - z(t) 和 u(t) 是状态网络的输入(对于时不变系统)。预测值 z(t+1) 是离散时间系统的输出。你训练一个状态网络来学习一个状态转换函数,该函数将 z(t) 映射到 z(t+1)。
Decoder - z(t+1) 是解码器的输入。x(t+1) 是解码器的输出,即重建后的状态。解码器将潜在状态空间映射回原始状态空间。
Output Network - 输出 y(t) 包含两部分。输出函数的第一部分是 y1(t)
=x(t),这意味着对态的直接测量。对于第二部分,经过训练的输出神经网络将输入信号 z(t) 和 u(t) 映射到输出信号 y2(t)(适用于时不变系统)。输出函数的第二部分仅在测量输出数量大于状态数量时存在。
具有自编码器的时变离散时间神经状态空间模型具有以下一般形式:
其中 e 是编码器函数,f 是状态函数,d 是解码器函数,g 是非平凡输出函数。
同样地,具有自编码器的时变连续时间神经状态空间模型具有以下形式:
另请参阅
对象
idNeuralStateSpace|nssTrainingADAM|nssTrainingSGDM|nssTrainingRMSProp|nssTrainingLBFGS|idss|idnlgrey
函数
createMLPNetwork|setNetwork|nssTrainingOptions|nlssest|generateMATLABFunction|idNeuralStateSpace/evaluate|idNeuralStateSpace/linearize|sim