求解刚性晶体管微分代数方程

打开实时脚本

此示例说明如何求解描述电路的刚性微分代数方程 (DAE) [1]。在示例文件 amp1dae.m 中编码的单晶体管放大器问题可以重写为半显式形式，但本示例采用它的原始形式 $M u^{'} = ϕ (u)$ 进行求解。该问题包括一个常奇异质量矩阵 $M$ 。

晶体管放大器电路包含六个电阻器、三个电容器和一个晶体管。

初始电压信号为 $U_{e} (t) = 0.4 \sin (200 π t)$ 。
工作电压为 $U_{b} = 6$ 。
节点处的电压由 $U_{i} (t) (i = 1, 2, 3, 4, 5)$ 给出。
电阻 $R_{i} (i = 1, 2, 3, 4, 5, 6)$ 的值是常量，通过每个电阻的电流满足 $I = U / R$ 。
电容 $C_{i} (i = 1, 2, 3)$ 的值是常量，通过每个电容的电流满足 $I = C \cdot dU / dt$ 。

目标是求解通过节点 5 的输出电压， $U_{5} (t)$ 。

要在 MATLAB® 中求解此方程，您可以使用 ode 对象并设置此对象的属性来定义方程、质量矩阵和初始条件。然后，使用 solve 方法仿真系统随时间的变化。您可以将所需的函数作为函数包含在脚本中（如此处所示），或者将它们作为单独的命名文件保存在 MATLAB 路径上的目录中。

编写质量矩阵代码

根据基尔霍夫定律均衡通过每个节点（1 到 5）的电流，可以得到包含五个描述电路的方程的方程组：

$\begin{array}{l} node 1 : \frac{U_{e} (t)}{R_{0}} - \frac{U_{1}}{R_{0}} + C_{1} ({U_{2}}^{'} - {U_{1}}^{'}) = 0, \\ node 2 : \frac{U_{b}}{R_{2}} - U_{2} (\frac{1}{R_{1}} + \frac{1}{R_{2}}) + C_{1} ({U_{1}}^{'} - {U_{2}}^{'}) - 0.01 f (U_{2} - U_{3}) = 0, \\ node 3 : f (U_{2} - U_{3}) - \frac{U_{3}}{R_{3}} - C_{2} {U_{3}}^{'} = 0, \\ node 4 : \frac{U_{b}}{R_{4}} - \frac{U_{4}}{R_{4}} + C_{3} ({U_{5}}^{'} - {U_{4}}^{'}) - 0.99 f (U_{2} - U_{3}) = 0, \\ node 5 : - \frac{U_{5}}{R_{5}} + C_{3} ({U_{4}}^{'} - {U_{5}}^{'}) = 0 . \end{array}$

此方程组的质量矩阵通过聚合方程左侧的导数项得到，其形式如下

$M = (\begin{array}{ccccc} - c_{1} & c_{1} & 0 & 0 & 0 \\ c_{1} & - c_{1} & 0 & 0 & 0 \\ 0 & 0 & - c_{2} & 0 & 0 \\ 0 & 0 & 0 & - c_{3} & c_{3} \\ 0 & 0 & 0 & c_{3} & - c_{3} \end{array}),$

其中，当 $k = 1, 2, 3$ 时， $c_{k} = k \times 1 0^{- 6}$ 。

用适当的常量 $c_{k}$ 创建一个质量矩阵，然后创建一个 odeMassMatrix 对象来存储该质量矩阵。尽管质量矩阵显然是奇异矩阵，请仍保留 Singular 属性的默认值 "maybe"，以测试求解器对 DAE 问题的自动检测。

c = 1e-6 * (1:3);
M = zeros(5,5);
M(1,1) = -c(1);
M(1,2) =  c(1);
M(2,1) =  c(1);
M(2,2) = -c(1);
M(3,3) = -c(2);
M(4,4) = -c(3);
M(4,5) =  c(3);
M(5,4) =  c(3);
M(5,5) = -c(3);
Mass = odeMassMatrix(MassMatrix=M);

编写方程代码

函数 transampdae 包含此示例的方程组。该函数定义所有电压和常量参数的值。在质量矩阵中对在方程左侧聚合的导数编码，而 transampdae 对方程的右侧编码。

function dudt = transampdae(t,u)
% Define voltages and parameters
Ue = @(t) 0.4*sinpi(200*t);
Ub = 6;
R0 = 1000;
R15 = 9000;
alpha = 0.99;
beta = 1e-6;
Uf = 0.026;

% Define system of equations
f23 = beta*(exp((u(2) - u(3))/Uf) - 1);
dudt = [ -(Ue(t) - u(1))/R0
    -(Ub/R15 - u(2)*2/R15 - (1-alpha)*f23)
    -(f23 - u(3)/R15)
    -((Ub - u(4))/R15 - alpha*f23)
    (u(5)/R15) ];
end

编写初始条件代码

设置初始条件。此示例对通过 [1] 中计算的每个节点的电流使用一致初始条件。

Ub = 6;
u0(1) = 0;
u0(2) = Ub/2;
u0(3) = Ub/2;
u0(4) = Ub;
u0(5) = 0;

求解方程组

创建一个 ode 对象来描述问题，设置 ODEFcn、MassMatrix 和 InitialValue 属性的值。另外，选择 ode23t 求解器来求解问题。

F = ode(ODEFcn=@transampdae,MassMatrix=Mass,InitialValue=u0,Solver="ode23t")

F = 
  ode with properties:

   Problem definition
               ODEFcn: @transampdae
          InitialTime: 0
         InitialValue: [0 3 3 6 0]
             Jacobian: []
           MassMatrix: [1x1 odeMassMatrix]
         EquationType: standard

   Solver properties
    AbsoluteTolerance: 1.0000e-06
    RelativeTolerance: 1.0000e-03
               Solver: ode23t

  Show all properties

使用 solve 方法求出 DAE 方程组在时间区间 [0 0.05] 内的解。

S = solve(F,0,0.05);
t = S.Time;
u = S.Solution;

绘制结果

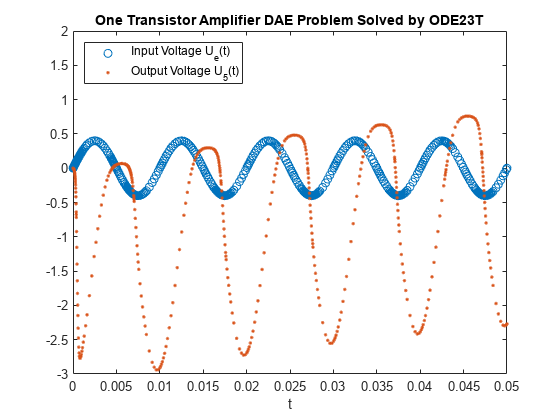
绘制通过节点 5 的初始电压 $U_{e} (t)$ 和输出电压 $U_{5} (t)$ 。

Ue = @(t) 0.4*sinpi(200*t);
plot(t,Ue(t),"o",t,u(5,:),".")
axis([0 0.05 -3 2]);
legend("Input Voltage U_e(t)","Output Voltage U_5(t)",Location="NorthWest");
title("One Transistor Amplifier DAE Problem Solved by ODE23T");
xlabel("t");

Figure contains an axes object. The axes object with title One Transistor Amplifier DAE Problem Solved by ODE23T, xlabel t contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Input Voltage U_e(t), Output Voltage U_5(t).

参考

[1] Hairer, E., and Gerhard Wanner.Solving Ordinary Differential Equations II:Stiff and Differential-Algebraic Problems.Springer Berlin Heidelberg, 1991, p. 377.

另请参阅

ode23t | ode15s