Main Content

稀疏矩阵重新排序

打开实时脚本

此示例说明对稀疏矩阵的各行和列重新排序可能会影响矩阵运算所需的速度和存储空间要求。

可视化稀疏矩阵

spy 图可以显示矩阵中的非零元素。

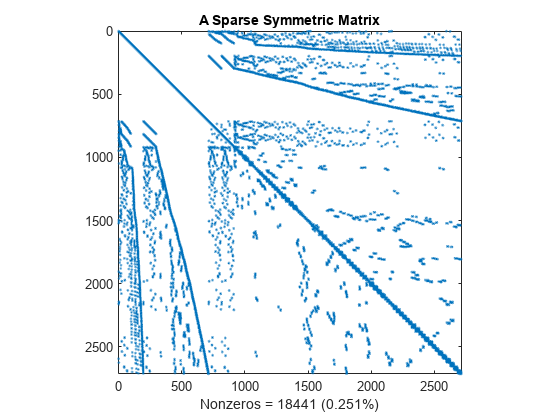
下面的 spy 图显示了从杠铃矩阵的一部分得到的稀疏对称正定矩阵。此矩阵描述类似杠铃的图中的连接。

load barbellgraph.mat
S = A + speye(size(A));
pct = 100 / numel(A);
spy(S)
title('A Sparse Symmetric Matrix')
nz = nnz(S);
xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));

Figure contains an axes object. The axes object with title A Sparse Symmetric Matrix, xlabel Nonzeros = 18441 (0.251%) contains a line object which displays its values using only markers.

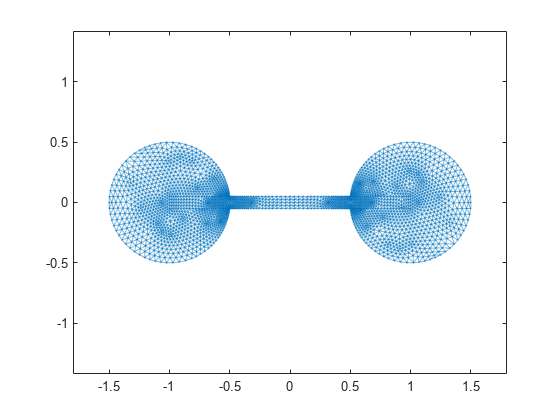
以下是杠铃图。

G = graph(S,'omitselfloops');
p = plot(G,'XData',xy(:,1),'YData',xy(:,2),'Marker','.');
axis equal

Figure contains an axes object. The axes object contains an object of type graphplot.

计算乔列斯基因子

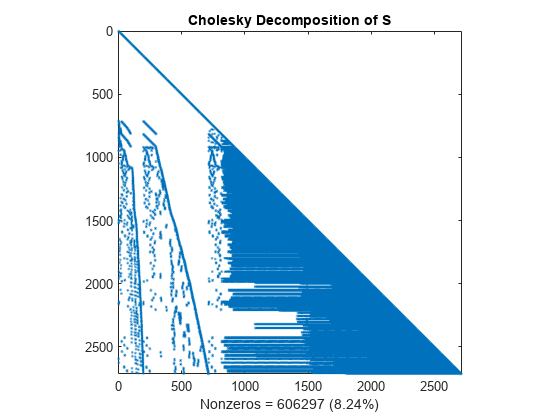
计算乔列斯基因子 L，其中 S = L*L'。请注意，L 比未分解的 S 包含更多的非零元素，因为计算乔列斯基分解产生了填充非零值。这些填充值会降低算法速度并增加存储成本。

L = chol(S,'lower');
spy(L)
title('Cholesky Decomposition of S')
nc(1) = nnz(L);
xlabel(sprintf('Nonzeros = %d (%.2f%%)',nc(1),nc(1)*pct));

Figure contains an axes object. The axes object with title Cholesky Decomposition of S, xlabel Nonzeros = 606297 (8.24%) contains a line object which displays its values using only markers.

重新排序以加快计算速度

通过对矩阵的各行和各列重新排序，有可能减少由于分解而产生的填充值数量，从而降低后续计算的时间和存储成本。

MATLAB® 支持若干种不同的重新排序方法：

  • colperm:列计数

  • symrcm:反向卡西尔-麦基排序

  • amd:最小度

  • dissect:嵌套剖分

测试这些稀疏矩阵重新排序方法对杠铃矩阵的影响。

列计数重新排序

colperm 命令使用列计数重新排序算法将非零计数较大的行和列移向矩阵的末尾。

q = colperm(S);
spy(S(q,q))
title('S(q,q) After Column Count Ordering')
nz = nnz(S);
xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));

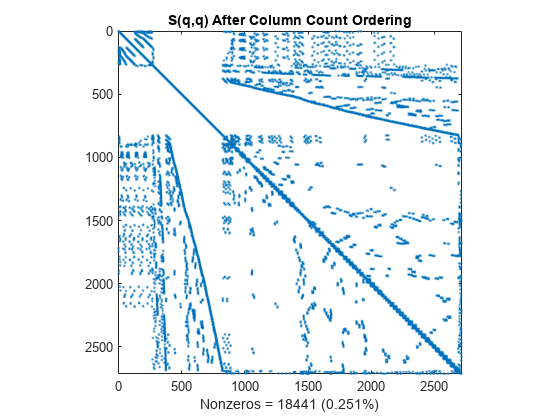
Figure contains an axes object. The axes object with title S(q,q) After Column Count Ordering, xlabel Nonzeros = 18441 (0.251%) contains a line object which displays its values using only markers.

对于此矩阵，列计数排序几乎无法减少乔列斯基分解的时间和存储量。

L = chol(S(q,q),'lower');
spy(L)
title('chol(S(q,q)) After Column Count Ordering')
nc(2) = nnz(L);
xlabel(sprintf('Nonzeros = %d (%.2f%%)',nc(2),nc(2)*pct));

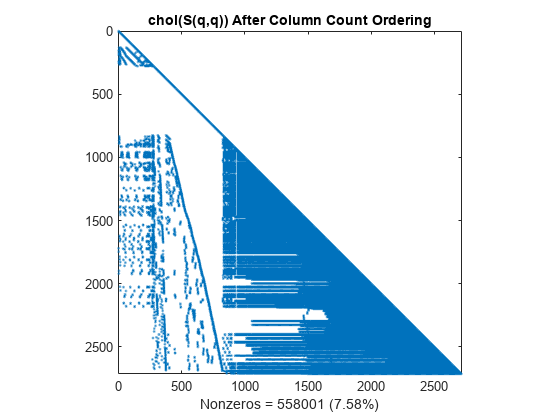
Figure contains an axes object. The axes object with title chol(S(q,q)) After Column Count Ordering, xlabel Nonzeros = 558001 (7.58%) contains a line object which displays its values using only markers.

反向卡西尔-麦基重新排序

symrcm 命令使用反向卡西尔-麦基重新排序算法将所有非零元素移至更靠近对角线的位置，从而减小原始矩阵的带宽。

d = symrcm(S);
spy(S(d,d))
title('S(d,d) After Cuthill-McKee Ordering')
nz = nnz(S);
xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));

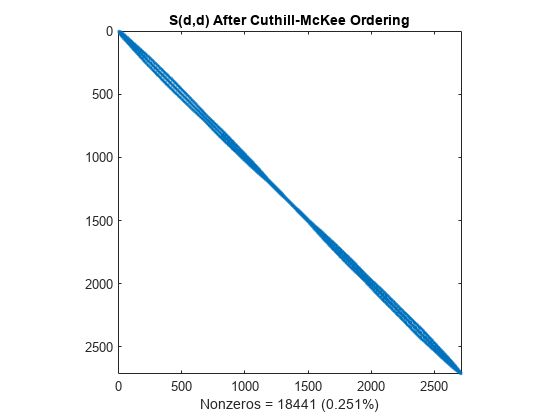
Figure contains an axes object. The axes object with title S(d,d) After Cuthill-McKee Ordering, xlabel Nonzeros = 18441 (0.251%) contains a line object which displays its values using only markers.

乔列斯基分解产生的填充值被限制在该带宽内，因此分解重新排序后的矩阵需要的时间和存储空间较少。

L = chol(S(d,d),'lower');
spy(L)
title('chol(S(d,d)) After Cuthill-McKee Ordering')
nc(3) = nnz(L);
xlabel(sprintf('Nonzeros = %d (%.2f%%)', nc(3),nc(3)*pct));

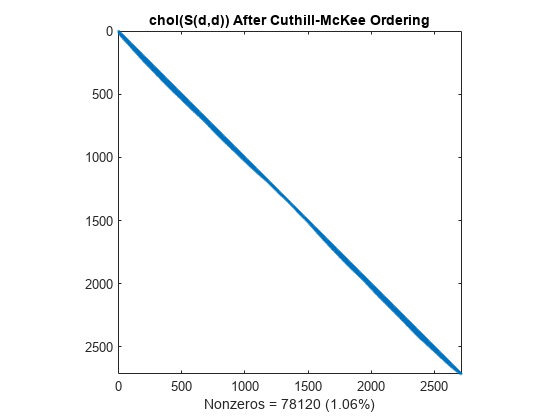
Figure contains an axes object. The axes object with title chol(S(d,d)) After Cuthill-McKee Ordering, xlabel Nonzeros = 78120 (1.06%) contains a line object which displays its values using only markers.

最小度重新排序

amd 命令使用一种近似最小度算法（一种非常有用的图论技巧）在矩阵中产生大块的零。

r = amd(S);
spy(S(r,r))
title('S(r,r) After Minimum Degree Ordering')
nz = nnz(S);
xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));

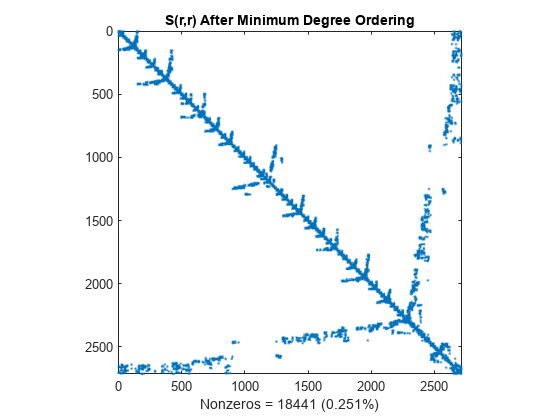
Figure contains an axes object. The axes object with title S(r,r) After Minimum Degree Ordering, xlabel Nonzeros = 18441 (0.251%) contains a line object which displays its values using only markers.

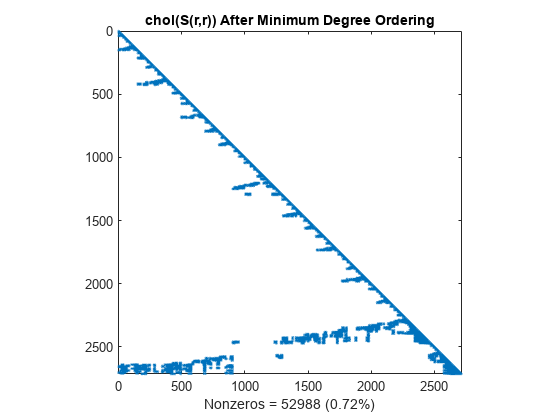
乔列斯基分解会保留最小度算法产生的各块零。此结构可以显著降低时间和存储成本。

L = chol(S(r,r),'lower');
spy(L)
title('chol(S(r,r)) After Minimum Degree Ordering')
nc(4) = nnz(L);
xlabel(sprintf('Nonzeros = %d (%.2f%%)',nc(4),nc(4)*pct));

Figure contains an axes object. The axes object with title chol(S(r,r)) After Minimum Degree Ordering, xlabel Nonzeros = 52988 (0.72%) contains a line object which displays its values using only markers.

嵌套剖分置换

dissect 函数使用图论方法来生成减少填充的排序。该算法将矩阵视为图的邻接矩阵，通过折叠顶点和边来粗化图，重排较小的图，然后通过细化步骤对小图去粗，得到重排的原始图。结果将得到一个功能强大的算法，与其他重新排序算法相比，它往往产生最少的填充量。

p = dissect(S);
spy(S(p,p))
title('S(p,p) After Nested Dissection Ordering')
nz = nnz(S);
xlabel(sprintf('Nonzeros = %d (%.3f%%)',nz,nz*pct));

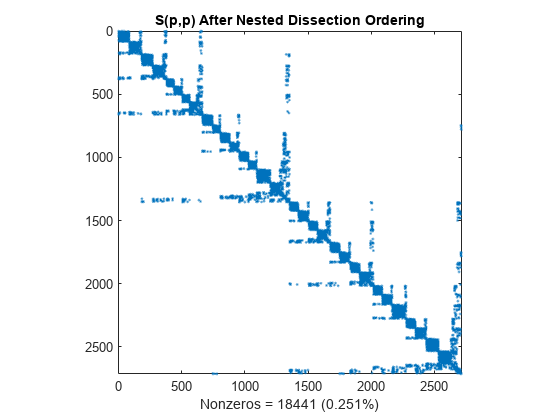
Figure contains an axes object. The axes object with title S(p,p) After Nested Dissection Ordering, xlabel Nonzeros = 18441 (0.251%) contains a line object which displays its values using only markers.

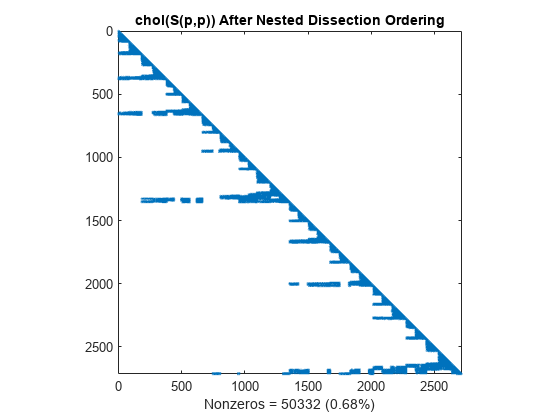
与最小度排序相似，嵌套剖分排序的乔列斯基分解最大程度地保留主对角线下方的 S(d,d) 非零结构体。

L = chol(S(p,p),'lower');
spy(L)
title('chol(S(p,p)) After Nested Dissection Ordering')
nc(5) = nnz(L);
xlabel(sprintf('Nonzeros = %d (%.2f%%)',nc(5),nc(5)*pct));

Figure contains an axes object. The axes object with title chol(S(p,p)) After Nested Dissection Ordering, xlabel Nonzeros = 50332 (0.68%) contains a line object which displays its values using only markers.

汇总结果

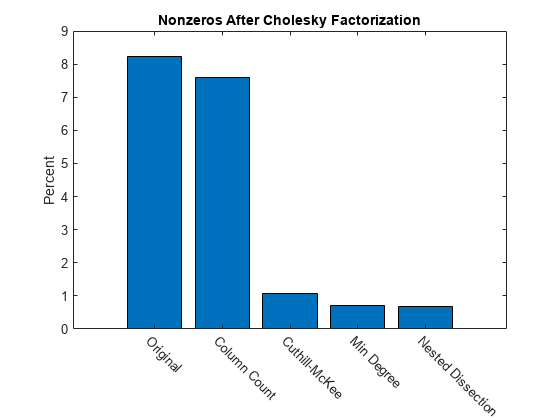
下面的条形图总结了执行乔列斯基分解之前对矩阵重新排序所带来的影响。虽然原始矩阵的乔列斯基分解约有 8% 的元素非零，但使用 dissect 或 symamd 可将该密度降至低于 1%。

labels = {'Original','Column Count','Cuthill-McKee',...
    'Min Degree','Nested Dissection'};
bar(nc*pct)
title('Nonzeros After Cholesky Factorization')
ylabel('Percent');
ax = gca;
ax.XTickLabel = labels;
ax.XTickLabelRotation = -45;

Figure contains an axes object. The axes object with title Nonzeros After Cholesky Factorization, ylabel Percent contains an object of type bar.

另请参阅

| | | | |