symamd

对称近似最小度置换

全页折叠

语法

p = symamd(S)
p = symamd(S,knobs)
[p,stats] = symamd(...)

说明

p = symamd(S)（对于对称正定矩阵 S）返回置换向量 p，这样 S(p,p) 倾向于比 S 具有更稀疏的乔列斯基因子。要计算 S 的排序，symamd 构造一个矩阵 M，这样 spones(M'*M) = spones (S)，然后计算 p = colamd(M)。symamd 函数也可能适用于对称非正定矩阵。

S 必须是方阵；仅引用严格下三角部分。

p = symamd(S,knobs)，其中 knobs 为标量。如果 S 为 n×n，则排序前，将会删除包含多个 knobs*n 项的行和列，并最后在输出置换 p 中排序。如果 knobs 参数不存在，则 knobs = spparms('wh_frac')。

[p,stats] = symamd(...) 生成可选的向量 stats，后者提供有关矩阵 S 的排序和有效性的数据。

stats(1)

symamd 忽略的密集或空行的数目

stats(2)

symamd 忽略的密集或空列的数目

stats(3)

对 symamd 使用的内部数据结构体执行的垃圾回收的次数（大小约等于 8.4*nnz(tril(S,-1)) + 9n 个整数）

stats(4)

0（如果矩阵有效）或 1（如果无效）

stats(5)

未排序或包含重复项的最右侧列的索引，或者为 0（如果不存在此类列）

stats(6)

由 stats(5) 指定的列索引中上次看到的重复或无序行索引，或者为 0（如果不存在此类行索引）

stats(7)

重复和无序行索引的数目

尽管 MATLAB® 的内置函数生成有效的稀疏矩阵，但用户可能会使用 MATLAB C 或 Fortran API 构造一个无效稀疏矩阵并将其传递给 symamd。出于此原因，symamd 将验证 S 是否有效：

  • 如果一个行索引在同一列中出现两次或以上，symamd 将忽略重复项，继续处理，并提供有关 stats(4:7) 中的重复项的信息。

  • 如果列中的行索引是无序的，symamd 将对矩阵 S 的内部副本的每列进行排序（但不会修复输入矩阵 S），继续处理，并提供有关 stats(4:7) 中的无序项的信息。

  • 如果 S 始终无效，symamd 无法继续。将输出一条错误消息，并且不返回任何输出参量（p 或 stats）。

该排序后跟对称消去树后排序。

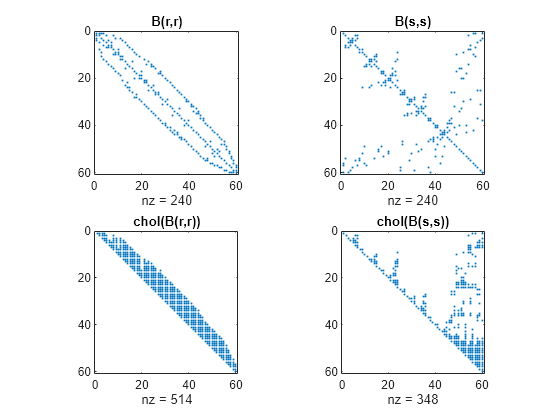
示例

全部折叠

打开实时脚本

此示例是关于反向卡西尔-麦基和最小度与 symrcm 参考页中提及的布基球示例的比较。

B = bucky+4*speye(60);
r = symrcm(B);
p = symamd(B);
R = B(r,r);
S = B(p,p);
subplot(2,2,1), spy(R,4), title('B(r,r)')
subplot(2,2,2), spy(S,4), title('B(s,s)')
subplot(2,2,3), spy(chol(R),4), title('chol(B(r,r))')
subplot(2,2,4), spy(chol(S),4), title('chol(B(s,s))')

Figure contains 4 axes objects. Axes object 1 with title B(r,r), xlabel nz = 240 contains a line object which displays its values using only markers. Axes object 2 with title B(s,s), xlabel nz = 240 contains a line object which displays its values using only markers. Axes object 3 with title chol(B(r,r)), xlabel nz = 514 contains a line object which displays its values using only markers. Axes object 4 with title chol(B(s,s)), xlabel nz = 348 contains a line object which displays its values using only markers.

尽管这是一个很小的问题，但两种排序的行为都很典型。RCM 生成一个具有窄带宽的矩阵，它在乔列斯基分解期间几乎完全填满。最小度算法生成一个包含大块连续零的结构体，这些块在分解期间不进行填充。因此，最小度排序需要的分解时间和存储空间都较少。

参考

[1] Davis, Timothy A., John R. Gilbert, Stefan I. Larimore, and Esmond G. Ng. “Algorithm 836: COLAMD, a Column Approximate Minimum Degree Ordering Algorithm.” ACM Transactions on Mathematical Software 30, no. 3 (September 2004): 377–380. https://doi.org/10.1145/1024074.1024080.

扩展功能

全部展开

版本历史记录

在 R2006a 之前推出

另请参阅

| | | | |