Main Content

colamd

Column approximate minimum degree permutation

collapse all in page

Syntax

p = colamd(S)
p = colamd(S,knobs)
[p,stats] = colamd(___)

Description

p = colamd(S) returns the column approximate minimum degree permutation vector for the sparse matrix S.

example

p = colamd(S,knobs) specifies thresholds for the maximum number of entries in the rows and columns of S before a row or column is ignored.

[p,stats] = colamd(___) specifies an additional output stats that provides data about the ordering and the validity of the matrix S.

Examples

collapse all

Open Live Script

The Harwell-Boeing collection of sparse matrices and the MATLAB® demos directory include a test matrix west0479. It is a matrix of order 479 resulting from a model due to Westerberg of an eight-stage chemical distillation column. The spy plot shows evidence of the eight stages. The colamd ordering scrambles this structure.

load west0479
A = west0479;
p = colamd(A);

figure()
subplot(1,2,1), spy(A,4), title('A')
subplot(1,2,2), spy(A(:,p),4), title('A(:,p)')

Figure contains 2 axes objects. Axes object 1 with title A, xlabel nz = 1887 contains a line object which displays its values using only markers. Axes object 2 with title A(:,p), xlabel nz = 1887 contains a line object which displays its values using only markers.

Comparing the spy plot of the LU factorization of the original matrix with that of the reordered matrix shows that minimum degree reduces the time and storage requirements by better than a factor of 2.8. The nonzero counts are 15918 and 5920, respectively.

figure()
subplot(1,2,1), spy(lu(A),4), title('lu(A)')
subplot(1,2,2), spy(lu(A(:,p)),4), title('lu(A(:,p))')

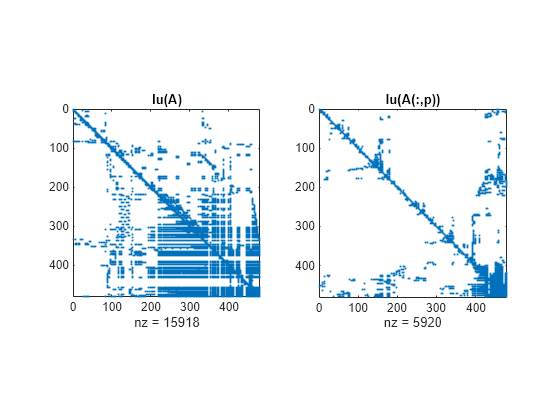
Figure contains 2 axes objects. Axes object 1 with title lu(A), xlabel nz = 15918 contains a line object which displays its values using only markers. Axes object 2 with title lu(A(:,p)), xlabel nz = 5920 contains a line object which displays its values using only markers.

Input Arguments

collapse all

Sparse matrix. Although MATLAB® built-in functions generate valid sparse matrices, it is possible to construct an invalid sparse matrix using the MATLAB C or Fortran APIs and pass it to colamd. For this reason, colamd verifies that S is a valid sparse matrix:

  • If a row index appears two or more times in the same column, colamd ignores the duplicate entries, continues processing, and provides information about the duplicate entries in stats(4:7).

  • If row indices in a column are out of order, colamd sorts each column of its internal copy of the matrix S (but does not repair the input matrix S), continues processing, and provides information about the out-of-order entries in stats(4:7).

  • If S is invalid in any other way, colamd cannot continue. It prints an error message, and returns no output arguments (p or stats).

Data Types: double | logical
Complex Number Support: Yes

Row and column thresholds, specified as a vector. knobs can have one to three elements:

  • Rows with more than max(16,knobs(1)*sqrt(size(S,2))) entries are ignored.

  • Columns with more than max(16,knobs(2)*sqrt(min(size(S)))) entries are ordered last in the output permutation p.

  • If knobs(1) or knobs(2) are less than 0, then only completely dense rows or columns are removed, respectively.

  • If knobs(3) is nonzero, then stats and knobs are printed.

Example: p = colamd(S,[10 5])

Output Arguments

collapse all

Permutation vector, returned as a numeric vector. For a non-symmetric matrix S, S(:,p) tends to have sparser LU factors than S. The Cholesky factorization of S(:,p)'*S(:,p) also tends to be sparser than that of S'*S.

The ordering is followed by a column elimination tree post-ordering.

Ordering information, returned as a vector. The stats vector contains information about the ordering performed and about the sparse input matrix S:

stats(1)

Number of dense or empty rows ignored by colamd

stats(2)

Number of dense or empty columns ignored by colamd

stats(3)

Number of garbage collections performed on the internal data structure used by colamd (roughly of size 2.2*nnz(S) + 4*m + 7*n integers)

stats(4)

0 if the matrix is valid, or 1 if invalid

stats(5)

Rightmost column index that is unsorted or contains duplicate entries, or 0 if no such column exists

stats(6)

Last seen duplicate or out-of-order row index in the column index given by stats(5), or 0 if no such row index exists

stats(7)

Number of duplicate and out-of-order row indices

The elements stats(4:7) are only relevant for input matrices S that were constructed using the MATLAB C or Fortran APIs. In this case, the elements diagnose whether such a matrix has invalid format. See the description of S for more information.

References

[1] Davis, Timothy A., John R. Gilbert, Stefan I. Larimore, and Esmond G. Ng. “Algorithm 836: COLAMD, a Column Approximate Minimum Degree Ordering Algorithm.” ACM Transactions on Mathematical Software 30, no. 3 (September 2004): 377–380. https://doi.org/10.1145/1024074.1024080.

Extended Capabilities

Version History

Introduced before R2006a

See Also

| | | |