Main Content

dissect

嵌套剖分置换

全页折叠

语法

p = dissect(A)
p = dissect(A,Name,Value)

说明

p = dissect(A) 返回一个使用 A 的稀疏结构的嵌套剖分计算的置换向量。

示例

p = dissect(A,Name,Value) 使用一个或多个名称-值对组参量指定其他选项。例如，dissect(A,'NumIterations',15) 在嵌套剖分算法中使用 15 次细化迭代，而不是 10 次。

示例

示例

全部折叠

打开实时脚本

用多种方法对稀疏矩阵重新排序，并比较重排矩阵的 LU 分解所产生的填充。

加载 west0479 矩阵，它是一个具有实数值的 479×479 稀疏矩阵，同时包含实共轭和复共轭特征值对。查看稀疏结构体。

load west0479.mat
A = west0479;
spy(A)

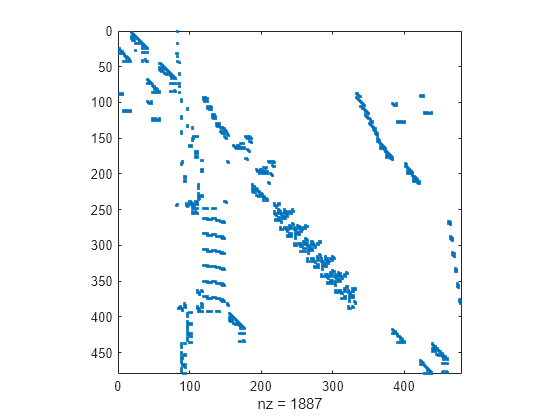
Figure contains an axes object. The axes object with xlabel nz = 1887 contains a line object which displays its values using only markers.

计算矩阵列的几种不同置换，包括嵌套剖分排序。

p1 = dissect(A);
p2 = amd(A);
p3 = symrcm(A);

使用不同的排序方法比较 A 的 LU 分解的稀疏结构。运行 dissect 函数产生的重新排序可使填充量最小。

subplot(1,2,1)
spy(A)
title('Original Matrix')
subplot(1,2,2)
spy(lu(A))
title('LU Decomposition')

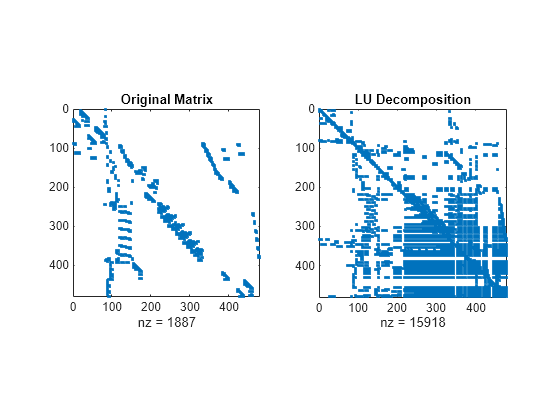
Figure contains 2 axes objects. Axes object 1 with title Original Matrix, xlabel nz = 1887 contains a line object which displays its values using only markers. Axes object 2 with title LU Decomposition, xlabel nz = 15918 contains a line object which displays its values using only markers.

figure
subplot(1,2,1)
spy(A(p3,p3))
title('Reverse Cuthill-McKee')
subplot(1,2,2)
spy(lu(A(p3,p3)))
title('LU Decomposition')

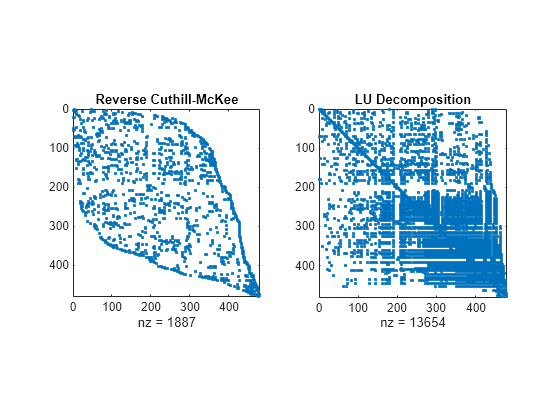
Figure contains 2 axes objects. Axes object 1 with title Reverse Cuthill-McKee, xlabel nz = 1887 contains a line object which displays its values using only markers. Axes object 2 with title LU Decomposition, xlabel nz = 13654 contains a line object which displays its values using only markers.

figure
subplot(1,2,1)
spy(A(p2,p2))
title('Approximate Minimum Degree')
subplot(1,2,2)
spy(lu(A(p2,p2)))
title('LU Decomposition')

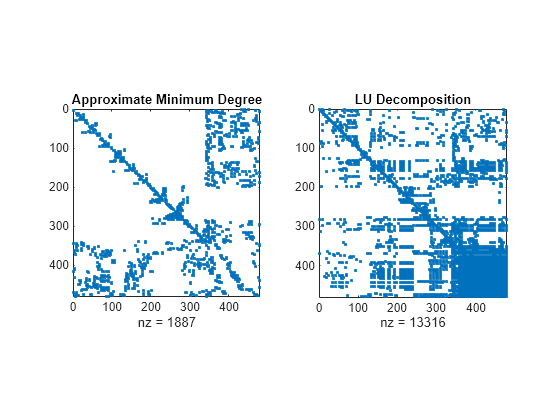
Figure contains 2 axes objects. Axes object 1 with title Approximate Minimum Degree, xlabel nz = 1887 contains a line object which displays its values using only markers. Axes object 2 with title LU Decomposition, xlabel nz = 13316 contains a line object which displays its values using only markers.

figure
subplot(1,2,1)
spy(A(p1,p1))
title('Nested Dissection')
subplot(1,2,2)
spy(lu(A(p1,p1)))
title('LU Decomposition')

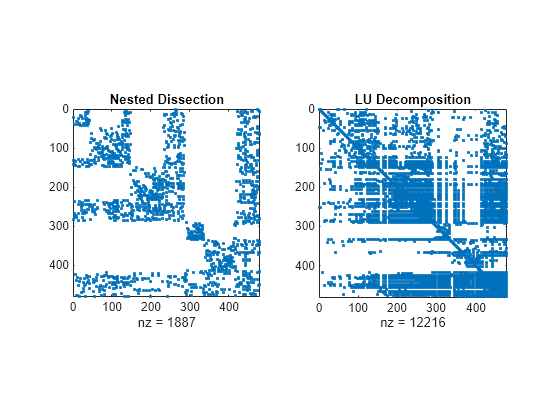
Figure contains 2 axes objects. Axes object 1 with title Nested Dissection, xlabel nz = 1887 contains a line object which displays its values using only markers. Axes object 2 with title LU Decomposition, xlabel nz = 12216 contains a line object which displays its values using only markers.

打开实时脚本

箭尖矩阵是包含若干密集列的稀疏矩阵。可以使用 'MaxDegreeThreshold' 名称-值对组将密集列过滤出来，放在重排矩阵的末尾。

创建一个箭尖稀疏矩阵并查看稀疏模式。

A = speye(100) + diag(ones(1,99),1) + diag(ones(1,98),2);
A(1:5,:) = ones(5,100);
A = A + A';
spy(A)

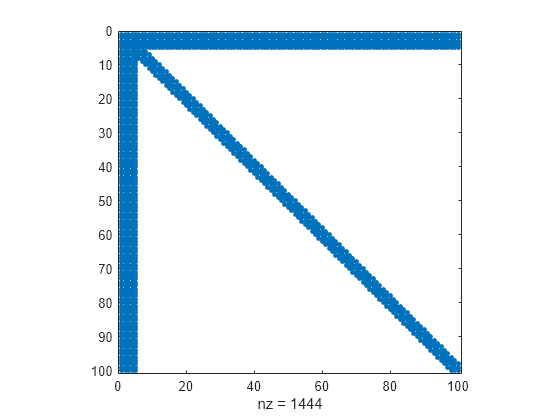
Figure contains an axes object. The axes object with xlabel nz = 1444 contains a line object which displays its values using only markers.

计算嵌套剖分排序，并过滤出具有 10 个以上非零元素的列。

p = dissect(A,'MaxDegreeThreshold',10);

查看重排矩阵的稀疏模式。dissect 将密集列放在重排矩阵的末尾。

spy(A(p,p))

Figure contains an axes object. The axes object with xlabel nz = 1444 contains a line object which displays its values using only markers.

输入参数

全部折叠

输入矩阵，指定为方阵。A 可以是满矩阵或稀疏矩阵。如果 A 不对称，dissect 会使它对称。

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
复数支持: 是

名称-值参数

将可选的参量对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但参量对组的顺序无关紧要。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: p = dissect(A,'NumIterations',15,'NumSeparators',2) 在嵌套剖分算法中使用 15 次细化迭代和 2 个分区。

顶点权重，指定为以逗号分隔的对组，其中包含 'VertexWeights' 和一个向量。权重向量的长度必须等于 size(A,1)，从而为每个顶点指定一个权重。使用此选项指定图形顶点（矩阵列）的加权方式，这会影响算法如何计算分区之间的平衡。

默认情况下，嵌套剖分算法对所有顶点平均加权。

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

分区的数量，指定为以逗号分隔的对组，其中包含 'NumSeparators' 和一个正整数。使用此选项可指定在每个分区步骤期间，图形分割的分区数量。在嵌套剖分算法中，增加分区的数量可以实现更高质量的置换，但会增加执行时间。

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

细化迭代的次数，指定为以逗号分隔的对组，其中包含 'NumIterations' 和一个正整数。在嵌套剖分算法中，增加细化迭代次数可以实现更高质量的置换，但会增加执行时间。

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

分区不平衡的阈值，指定为以逗号分隔的对组，其中包含 'MaxImbalance' 和一个标量值，此值是 0.001 的整数倍，大于或等于 1.001 且小于或等于 1.999。较大的阈值允许算法接受较差的置换，从而减少执行时间。

数据类型: single | double

顶点度数的阈值，指定为以逗号分隔的对组，其中包含 'MaxDegreeThreshold' 和一个非负整数。嵌套剖分算法将在排序时忽略度数大于 threshold*(avg degree)/10 的顶点。dissect 将在此过程中忽略的顶点放在置换的末尾。这样可以有效地将度数大于阈值的所有顶点放置在第一个顶层分区中。筛出高度连接的顶点有时可以提高排序的速度和准确性。

默认值 0 表示所有顶点都参与排序。

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

输出参量

全部折叠

置换向量，以向量形式返回。使用置换向量对使用索引表达式 A(p,p) 的 A 的各列进行重新排序。例如，乔列斯基分解 chol(A(p,p)) 可能比 A 更稀疏。

算法

[1] 中介绍的嵌套剖分排序算法是一种多级图形分区算法，用于对稀疏矩阵进行减少填充量的排序。输入矩阵被视为图形的邻接矩阵。该算法通过折叠顶点和边来粗化图形，重排较小的图形，然后通过细化步骤对较小图形去粗，得到重排的原始图形。

dissect 的名称-值对组使您能够控制算法的各个阶段：

  • 粗化

    在此阶段，算法将相邻的顶点对组折叠，从原始图生成连续的更小的图。您可以借助 'MaxDegreeThreshold'，最后再对高度连接的图顶点（矩阵中的密集列）进行排序，以将它们过滤出来。

  • 分区

    在图形粗化后，算法对更小的图形彻底重新排序。在每个分区步骤中，算法尝试将图形分成相等的部分：'NumSeparators' 指定将图形分成多少部分，'VertexWeights' 为顶点分配权重（可选），而 'MaxImbalance' 指定不同分区之间权重差的阈值。

  • 细化

    在对最小的图形重新排序后，算法展开之前合并的顶点进行投影，将图形放大到原始大小。在每个投影步骤后，执行细化步骤，移除分区之间的顶点，以提高解的质量。'NumIterations' 控制该去粗阶段使用的细化步骤的数量。

参考

[1] Karypis, George and Vipin Kumar. "A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs." SIAM Journal on Scientific Computing. Vol. 20, Number 1, 1999, pp. 359–392.

扩展功能

版本历史记录

在 R2017b 中推出

另请参阅

| | | |

主题