symrcm

稀疏反向卡西尔-麦基排序

语法

r = symrcm(S)

说明

r = symrcm(S) 返回 S 的对称反向卡西尔-麦基排序。此置换向量 r 使得 S(r,r) 可能会使其非零元素更接近于对角线。对于源自长、瘦问题的矩阵的 LU 或乔列斯基分解来说，这是一种很好的预排序方法。该排序方法对于对称和不对称 S 都有效。

对于实对称稀疏矩阵 S，S(r,r) 的特征值与 S 的特征值相同，但 eig(S(r,r)) 可能比 eig(S) 花费的计算时间更短。

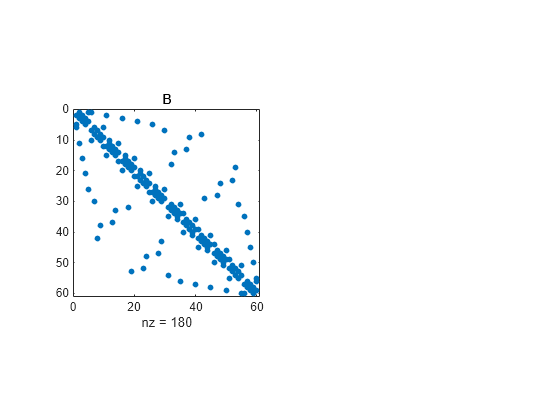
示例

全部折叠

反向卡西尔-麦基排序

打开实时脚本

语句

B = bucky;

使用 demos 工具箱中的函数生成截顶二十面体的邻接图。这更适合称为足球、巴克敏斯特·富勒多面穹顶（由此命名为 bucky），或者近来称为由 60 个原子组成的碳分子。顶点有 60 个。这些顶点已通过以下方式进行排序：逐五角形对一个半球中的半数顶点进行编号，然后映射到另一个半球并将两个半球粘合在一起。

通过这种编号，矩阵的带宽就不会特别窄，如第一个 spy 图所示：

figure();
subplot(1,2,1),spy(B),title('B')

Figure contains an axes object. The axes object with title B, xlabel nz = 180 contains a line object which displays its values using only markers.

反向卡西尔-麦基排序可通过以下命令获取：

p = symrcm(B);
R = B(p,p);

spy 图显示了更窄的带宽。

subplot(1,2,2),spy(R),title('B(p,p)')

Figure contains 2 axes objects. Axes object 1 with title B, xlabel nz = 180 contains a line object which displays its values using only markers. Axes object 2 with title B(p,p), xlabel nz = 180 contains a line object which displays its values using only markers.

symamd 的参考页中会继续对此示例进行说明。

带宽也可以通过以下命令进行计算：

[i,j] = find(B);
bw = max(i-j) + 1;

B 和 R 的带宽分别为 35 和 12。

算法

该算法首先找到矩阵图的伪外部顶点。然后，进行广度优先搜索生成一个层次结构体，并通过减少与伪外部顶点的距离来对各顶点排序。该实现严密地基于 George 和 Liu 所述的 SPARSPAK 实现。

参考

[1] George, Alan and Joseph Liu, Computer Solution of Large Sparse Positive Definite Systems, Prentice-Hall, 1981.

[2] Gilbert, John R., Cleve Moler, and Robert Schreiber, “Sparse Matrices in MATLAB: Design and Implementation,” SIAM Journal on Matrix Analysis, 1992. A slightly expanded version is also available as a technical report from the Xerox Palo Alto Research Center.