随着参数的变化，遵循方程解

此示例展示了如何随着参数的变化通过从前一个解点开始后续解重复求解方程。通常这个过程会产生有效的解。然而，解有时会消失，需要从一个或多个新点开始。

参数化标量方程

要求解的参数化方程是

$\sinh (x) - 3 x = a$ ,

其中 $a$ 是一个从 0 到 5 的数字参数。在 $a = 0$ 处，这个方程的一个解是 $x = 0$ 。当 $a$ 的绝对值不是太大时，该方程有三个解。为了使等式可视化，请将等式的左边创建为匿名函数。绘制函数。

fun = @(x)sinh(x) - 3*x;
t = linspace(-3.5,3.5);
plot(t,fun(t),t,zeros(size(t)),'k-')
xlabel('x')
ylabel('fun(x)')

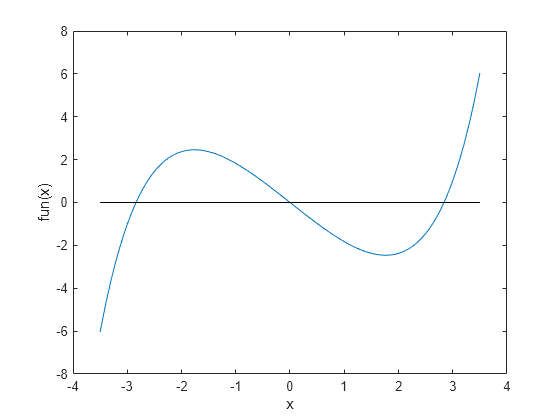
Figure contains an axes object. The axes object with xlabel x, ylabel fun(x) contains 2 objects of type line.

当 $a$ 太大或太小时，只有一个解。

基于问题的设置

要为基于问题的方法创建目标函数，请在优化变量 expr 中创建优化表达式 x。

x = optimvar('x');
expr = sinh(x) - 3*x;

创建并绘制解

从 $x = 0$ 处的初始解 $a = 0$ 开始，找到从 0 到 5 的 100 个 $a$ 值的解。因为 fun 是标量非线性函数，所以 solve 调用 fzero 作为求解器。

设置问题对象、选项和数据结构以保存解统计数据。

prob = eqnproblem;
options = optimset('Display','off');
sols = zeros(100,1);
fevals = sols;
as = linspace(0,5);

从第一个解 sols(1) = 0 开始，循环求解方程。

for i = 2:length(as)
    x0.x = sols(i-1); % Start from previous solution
    prob.Equations = expr == as(i);
    [sol,~,~,output] = solve(prob,x0,'Options',options);
    sols(i) = sol.x;
    fevals(i) = output.funcCount;
end

将解绘制为参数 a 的函数以及达到解所需的函数计算次数。

subplot(2,1,1)
plot(as,sols,'ko')
xlabel 'a'
ylabel('Solution(x)')
subplot(2,1,2)
plot(fevals,'k*')
xlabel('Iteration Number')
ylabel('Fevals')

Figure contains 2 axes objects. Axes object 1 with xlabel a, ylabel Solution(x) contains a line object which displays its values using only markers. Axes object 2 with xlabel Iteration Number, ylabel Fevals contains a line object which displays its values using only markers.

解中的跳跃发生在 $a = 2.5$ 附近。同时，达到解的函数计算次数从接近 15 次增加到接近 40 次。要了解原因，请检查函数的更详细图。绘制函数和每七个解点。

figure
t = linspace(-3.5,3.5);
plot(t,fun(t));
hold on
plot([-3.5,min(sols)],[2.5,2.5],'k--')
legend('fun','Maximum a','Location','north','autoupdate','off')
for a0 = 7:7:100
    plot(sols(a0),as(a0),'ro')
    if mod(a0,2) == 1
        text(sols(a0) + 0.15,as(a0) + 0.15,num2str(a0/7))
    else
        text(sols(a0) - 0.3,as(a0) + 0.05,num2str(a0/7))
    end
end
plot(t,zeros(size(t)),'k-')
hold off

Figure contains an axes object. The axes object contains 31 objects of type line, text. One or more of the lines displays its values using only markers These objects represent fun, Maximum a.

随着 $a$ 的增加，解首先向左移动。然而，当 $a$ 高于 2.5 时，在前一个解附近不再存在解。fzero 需要额外的函数计算来寻找解，并在 x = 3 附近找到一个解。此后，随着 $a$ 的进一步增加，解的值缓慢向右移动。求解器对于每个后续解仅需要大约 10 次函数计算。

选择不同的求解器

fsolve 求解器比 fzero 更高效。然而，fsolve 可能会陷入局部最小值并无法求解方程。

设置问题对象、选项和数据结构以保存解统计数据。

probfsolve = eqnproblem;
sols = zeros(100,1);
fevals = sols;
infeas = sols;
asfsolve = linspace(0,5);

从第一个解 sols(1) = 0 开始，循环求解方程。

for i = 2:length(as)
    x0.x = sols(i-1); % Start from previous solution
    probfsolve.Equations = expr == asfsolve(i);
    [sol,fval,~,output] = solve(probfsolve,x0,'Options',options,'Solver','fsolve');
    sols(i) = sol.x;
    fevals(i) = output.funcCount;
    infeas(i) = fval;
end

将解绘制为参数 a 的函数以及达到解所需的函数计算次数。

subplot(2,1,1)
plot(asfsolve,sols,'ko',asfsolve,infeas,'r-')
xlabel 'a'
legend('Solution','Error of Solution','Location','best')
subplot(2,1,2)
plot(fevals,'k*')
xlabel('Iteration Number')
ylabel('Fevals')

Figure contains 2 axes objects. Axes object 1 with xlabel a contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Solution, Error of Solution. Axes object 2 with xlabel Iteration Number, ylabel Fevals contains a line object which displays its values using only markers.

fsolve 比 fzero 稍微高效一些，每次迭代需要大约 7 或 8 次函数计算。同样，当求解器在前一个值附近找不到解时，求解器需要进行更多的函数计算来寻找解。这一次搜寻没有成功。后续迭代大部分只需要进行少量函数计算，但却无法找到解。Error of Solution 图显示函数值 $f u n (x) - a$ 。

为了尝试克服局部最小值不是解的问题，当 fsolve 以负退出标志返回时，从不同的起点再次搜索。设置问题对象、选项和数据结构以保存解统计数据。

rng default % For reproducibility
sols = zeros(100,1);
fevals = sols;
asfsolve = linspace(0,5);

从第一个解 sols(1) = 0 开始，循环求解方程。

for i = 2:length(as)
    x0.x = sols(i-1); % Start from previous solution
    probfsolve.Equations = expr == asfsolve(i);
    [sol,~,exitflag,output] = solve(probfsolve,x0,'Options',options,'Solver','fsolve');
    
    while exitflag <= 0 % If fsolve fails to find a solution
        x0.x = 5*randn; % Try again from a new start point
        fevals(i) = fevals(i) + output.funcCount;
        [sol,~,exitflag,output] = solve(probfsolve,x0,'Options',options,'Solver','fsolve');
    end
    
    sols(i) = sol.x;
    fevals(i) = fevals(i) + output.funcCount;
end

将解绘制为参数 a 的函数以及达到解所需的函数计算次数。

subplot(2,1,1)
plot(asfsolve,sols,'ko')
xlabel 'a'
ylabel('Solution(x)')
subplot(2,1,2)
plot(fevals,'k*')
xlabel('Iteration Number')
ylabel('Fevals')

这次，fsolve 从 $a = 2.5$ 附近的较差的初始点恢复过来，并获得了与 fzero 类似的解。每次迭代的函数计算次数通常为 8 次，在解跳跃点处增加到大约 30 次。

使用 `fcn2optimexpr` 转换目标函数

对于某些目标函数或软件版本，您必须使用 fcn2optimexpr 将非线性函数转换为优化表达式。请参阅优化变量和表达式支持的运算和将非线性函数转换为优化表达式。对于此示例，将用于绘图的原始函数 fun 转换为优化表达式 expr：

expr = fcn2optimexpr(fun,x);

对 expr 的定义进行此项更改后，示例的其余部分完全相同。

另请参阅

fzero | fsolve | solve

随着参数的变化，遵循方程解

参数化标量方程

基于问题的设置

创建并绘制解

选择不同的求解器

使用 fcn2optimexpr 转换目标函数

另请参阅

主题

使用 `fcn2optimexpr` 转换目标函数