issatisfied
语法
说明
示例
创建一个具有若干线性和非线性约束的优化问题。
x = optimvar("x"); y = optimvar("y"); obj = (10*(y - x^2))^2 + (1 - x)^2; cons1 = x^2 + y^2 <= 1; cons2 = x + y >= 0; cons3 = y <= sin(x); cons4 = 2*x + 3*y <= 2.5; prob = optimproblem(Objective=obj); prob.Constraints.cons1 = cons1; prob.Constraints.cons2 = cons2; prob.Constraints.cons3 = cons3; prob.Constraints.cons4 = cons4;
随机创建 100 个测试点。
rng default % For reproducibility xvals = randn(1,100); yvals = randn(1,100);
将点转换为问题的 OptimizationValues 对象，并确定点中所有约束都得到满足的位置。
vals = optimvalues(prob,x=xvals,y=yvals); allsat = issatisfied(prob,vals);
用绿色圆圈绘制可行（满足）点，用红色 x 标记绘制不可行点。
xsat = xvals(allsat); ysat = yvals(allsat); xnosat = xvals(~allsat); ynosat = yvals(~allsat); plot(xsat,ysat,"go",xnosat,ynosat,"rx")
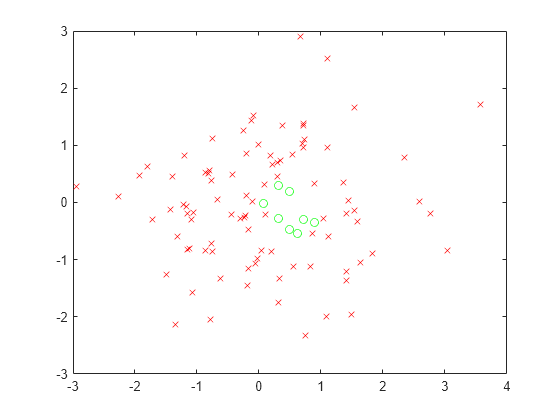
创建两个优化变量和一个 3×2 的不等式约束数组。
x = optimvar("x"); y = optimvar("y"); cons = optimconstr(3,2); cons(1,1) = x^2 + y^2/4 <= 2; cons(1,2) = 3*x + y <= 4; cons(2,1) = -x - y^3 <= -3; cons(2,2) = 2*x^2 + x*y + 4*y^2 <= 6; cons(3,1) = 2*x + 4*x*y + y^2 <= 5; cons(3,2) = (4 + x*y)^2 <= 24;
检查点 x = 1/2, y = -1/2 处是否满足所有约束。
pt.x = 1/2; pt.y = -1/2; allsat = issatisfied(cons,pt)
allsat = logical
0
并非所有约束都得到满足。找出哪些约束得到满足。
[allsat,sat] = issatisfied(cons,pt)
allsat = logical
0
sat = 3×2 logical array
1 1
0 1
1 1
除 constraint(2,1) 外，其他所有约束均得到满足。
创建一个具有若干线性和非线性约束的优化问题。
x = optimvar("x"); y = optimvar("y"); obj = (10*(y - x^2))^2 + (1 - x)^2; cons1 = x^2 + y^2 <= 1; cons2 = x + y >= 0; cons3 = y <= sin(x); cons4 = 2*x + 3*y <= 2.5; prob = optimproblem(Objective=obj); prob.Constraints.cons1 = cons1; prob.Constraints.cons2 = cons2; prob.Constraints.cons3 = cons3; prob.Constraints.cons4 = cons4;
随机创建 100 个测试点。
rng default % For reproducibility xvals = randn(1,100); yvals = randn(1,100);
将点转换为问题的 OptimizationValues 对象，并确定点中所有约束都得到满足的位置。
vals = optimvalues(prob,x=xvals,y=yvals); allsat = issatisfied(prob,vals);
用绿色圆圈绘制可行（满足）点，用红色 x 标记绘制不可行点。
xsat = xvals(allsat); ysat = yvals(allsat); xnosat = xvals(~allsat); ynosat = yvals(~allsat); plot(xsat,ysat,"go",xnosat,ynosat,"rx")
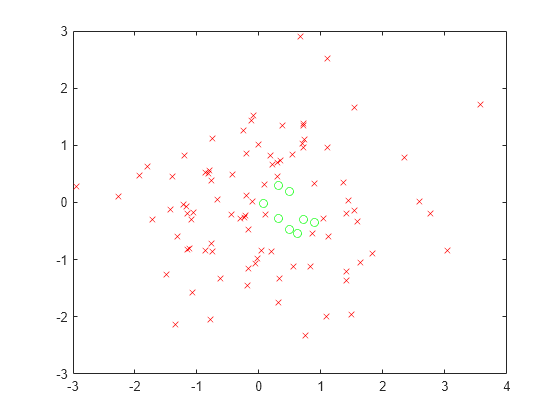
确定哪些点对于容差 1 而非默认值 1e-6 是可行的。
tol = 1; allsat1 = issatisfied(prob,vals,tol);
用绿色圆圈绘制可行（满足）点，用红色 x 标记绘制不可行点。
xsat1 = xvals(allsat1); ysat1 = yvals(allsat1); xnosat1 = xvals(~allsat1); ynosat1 = yvals(~allsat1); plot(xsat1,ysat1,"go",xnosat1,ynosat1,"rx")
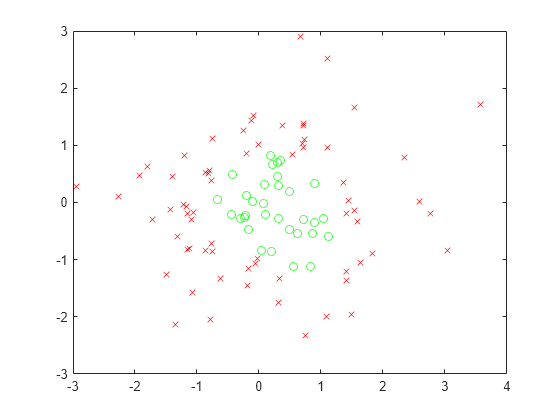
如果约束满足的定义较为宽松，则更多的点是可行的。
创建一个具有若干线性和非线性约束的优化问题。
x = optimvar("x"); y = optimvar("y"); obj = (10*(y - x^2))^2 + (1 - x)^2; cons1 = x^2 + y^2 <= 1; cons2 = x + y >= 0; cons3 = y <= sin(x); cons4 = 2*x + 3*y <= 2.5; prob = optimproblem(Objective=obj); prob.Constraints.cons1 = cons1; prob.Constraints.cons2 = cons2; prob.Constraints.cons3 = cons3; prob.Constraints.cons4 = cons4;
随机创建 100 个测试点。
rng default % For reproducibility xvals = randn(1,100); yvals = randn(1,100);
将这些点转换为问题的一个 OptimizationValues 对象。
vals = optimvalues(prob,x=xvals,y=yvals);
评估点处的约束。issatisfied 同时评估所有测试点处的所有约束满足情况。
[~,sat] = issatisfied(prob,vals);
用绿色圆圈绘制第一个约束的可行（满足）点，用红色 x 标记绘制不可行的点。
x1sat = xvals(sat.cons1); y1sat = yvals(sat.cons1); x1nosat = xvals(~sat.cons1); y1nosat = yvals(~sat.cons1); plot(x1sat,y1sat,"go",x1nosat,y1nosat,"rx") title("Constraint 1 Satisfaction")
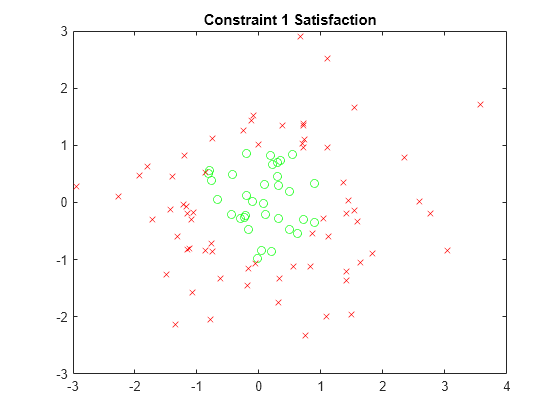
对其他三个约束重复此过程。
x2sat = xvals(sat.cons2); y2sat = yvals(sat.cons2); x2nosat = xvals(~sat.cons2); y2nosat = yvals(~sat.cons2); plot(x2sat,y2sat,"go",x2nosat,y2nosat,"rx") title("Constraint 2 Satisfaction")
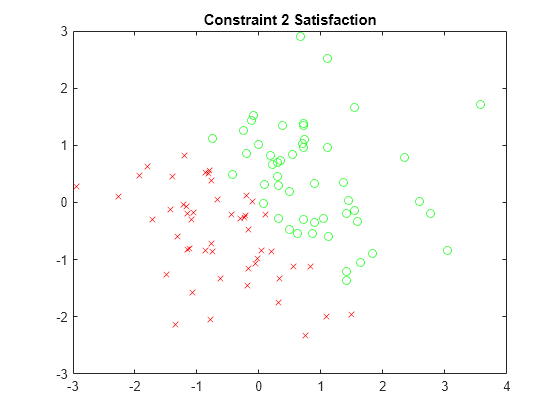
x3sat = xvals(sat.cons3); y3sat = yvals(sat.cons3); x3nosat = xvals(~sat.cons3); y3nosat = yvals(~sat.cons3); plot(x3sat,y3sat,"go",x3nosat,y3nosat,"rx") title("Constraint 3 Satisfaction")
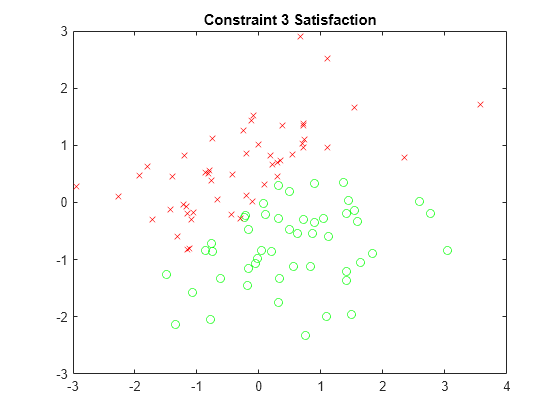
x4sat = xvals(sat.cons4); y4sat = yvals(sat.cons4); x4nosat = xvals(~sat.cons4); y4nosat = yvals(~sat.cons4); plot(x4sat,y4sat,"go",x4nosat,y4nosat,"rx") title("Constraint 4 Satisfaction")
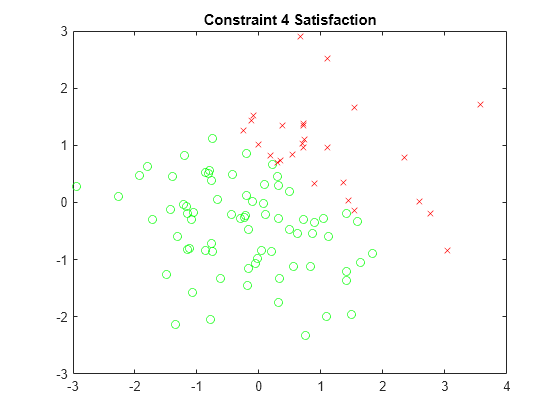
这些图显示了每个约束的不同的满足区域。
创建一组包含两个优化变量的方程。
x = optimvar("x"); y = optimvar("y"); prob = eqnproblem; prob.Equations.eq1 = x^2 + y^2/4 == 2; prob.Equations.eq2 = x^2/4 + 2*y^2 == 2;
从 开始解方程组。
x0.x = 1; x0.y = 1/2; sol = solve(prob,x0)
Solving problem using fsolve. Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details>
sol = struct with fields:
x: 1.3440
y: 0.8799
在点 x0 和 sol 处求方程。
vars = optimvalues(prob,x=[x0.x sol.x],y=[x0.y sol.y]); vals = evaluate(prob,vars)
vals =
1×2 OptimizationValues vector with properties:
Variables properties:
x: [1 1.3440]
y: [0.5000 0.8799]
Equation properties:
eq1: [0.9375 8.4322e-10]
eq2: [1.2500 6.7431e-09]
第一个点 x0 对于方程 eq1 和 eq2 都有非零值。第二点 sol 这些方程的值几乎为零，正如预期的那样，这是一个解。
使用 issatisfied 查找方程的满足度。
[satisfied details] = issatisfied(prob,vars)
satisfied = 1×2 logical array
0 1
details =
1×2 OptimizationValues vector with properties:
Variables properties:
x: [1 1.3440]
y: [0.5000 0.8799]
Equation properties:
eq1: [0 1]
eq2: [0 1]
第一个点 x0 不是解，并且 satisfied 该点的 0。第二点 sol 是一个解，且该点的 satisfied 为 1。方程属性表明，在第一点处两个方程都不满足，在第二点处两个方程均满足。
