Main Content

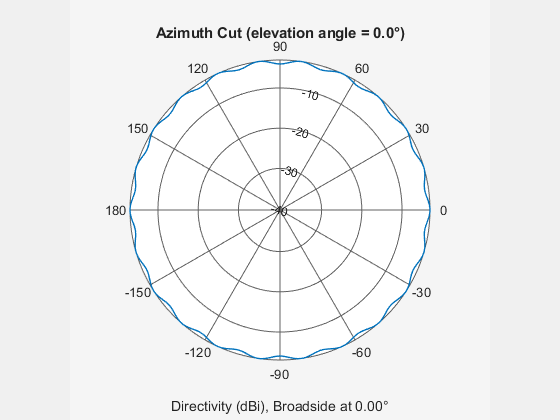
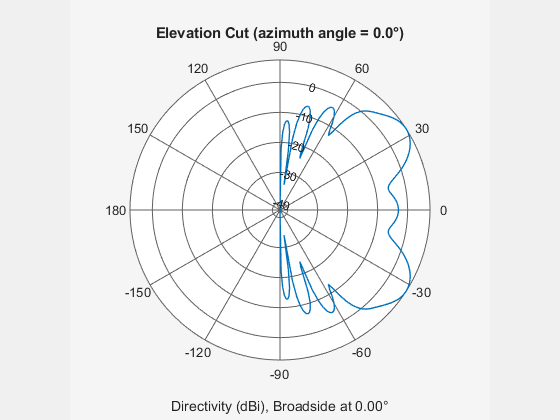
phased.UCA

Uniform circular array

expand all in page

Description

The phased.UCA System object™ creates a uniform circular array (UCA). A UCA is formed from identical sensor elements equally spaced around a circle.

To compute the response for the array for specified directions:

  1. Create the phased.UCA object and set its properties.

  2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

sUCA = phased.UCA
sUCA = phased.UCA(Name,Value)
sUCA = phased.UCA(N,R)
sUCA = phased.UCA(N,R,Name,Value)

Description

sUCA = phased.UCA creates a uniform circular array (UCA) System object, sUCA, consisting of five identical isotropic antenna elements,phased.IsotropicAntennaElement. The elements are equally spaced around a circle of radius 0.5 meters.

sUCA = phased.UCA(Name,Value) creates a System object, sUCA, with each specified property Name set to the specified Value. You can specify additional name-value pair arguments in any order as (Name1,Value1,...,NameN,ValueN).

example

sUCA = phased.UCA(N,R) creates a UCA System object, sUCA, with the NumElements property set to N and the Radius property set to R. This syntax creates a UCA consisting of isotropic antenna elements, phased.IsotropicAntennaElement.

sUCA = phased.UCA(N,R,Name,Value) creates a UCA System object, sUCA, with the NumElements property set to N, the Radius property set to R, and other specified property Names set to the specified Values.

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Phased array element, specified as a Phased Array System Toolbox antenna, microphone, or transducer element or Antenna Toolbox antenna.

Example: phased.CosineAntennaElement

Number of array elements, specified as an integer greater than one.

Example: 3

Array radius, specified as a positive scalar in meters.

Example: 2.5

Array normal direction, specified as one of 'x', 'y', or 'z'. UCA elements lie in a plane orthogonal to the array normal direction. Element boresight vectors lie in the same plane and point radially outward from the origin.

ArrayNormal Property ValueElement Positions and Boresight Directions
'x'Array elements lie on the yz-plane. All element boresight vectors lie in the yz-plane and point outward from the array center.
'y'Array elements lie on the zx-plane. All element boresight vectors lie in the zx-plane and point outward from the array center.
'z'Array elements lie on the xy-plane. All element boresight vectors lie in the xy-plane and point outward from the array center.

Example: 'y'

Element tapering or weighting, specified as a complex-valued scalar, 1-by-N row vector, or N-by-1 column vector. The quantity N represents the number of elements of the array. Tapers, also known as weights, are applied to each sensor element in the sensor array and modify both the amplitude and phase of the received data. If 'Taper' is a scalar, the same taper value is applied to all element. If 'Taper' is a vector, each taper value is applied to the corresponding sensor element.

Example: [1 2 3 2 1]

Usage

Syntax

RESP = sUCA(FREQ,ANG)

Description

RESP = sUCA(FREQ,ANG) returns the responses, RESP, of the array elements, at operating frequencies specified in FREQ and directions specified in ANG.

Note

The object performs an initialization the first time the object is executed. This initialization locks nontunable properties and input specifications, such as dimensions, complexity, and data type of the input data. If you change a nontunable property or an input specification, the System object issues an error. To change nontunable properties or inputs, you must first call the release method to unlock the object.

example

Input Arguments

expand all

Operating frequency of array specified, specified as a positive scalar or 1-by-L real-valued row vector. Frequency units are in hertz.

  • For antenna or microphone elements, FREQ must lie within the range of values specified by the FrequencyRange or FrequencyVector property of the element. Otherwise, the element produces no response and the array response is returned as zero. Most elements use the FrequencyRange property except for phased.CustomAntennaElement and phased.CustomMicrophoneElement, which use the FrequencyVector property.

  • For an array of elements, FREQ must lie within the frequency range of the elements that make up the array. Otherwise, the array produces no response and the directivity is returned as zero.

Example: [1e8 2e8]

Data Types: double

Response directions, specified as either a 2-by-M real-valued matrix or a real-valued row vector of length M.

If ANG is a 2-by-M matrix, each column of the matrix specifies the direction in the form [azimuth; elevation]. The azimuth angle must lie between –180° and 180°, inclusive. The elevation angle must lie between –90° and 90°, inclusive. Angle units are in degrees.

If ANG is a row vector of length M, each element specifies the azimuth angle of the direction. In this case, the corresponding elevation angle is assumed to be 0°.

Example: [20;15]

Data Types: double

Output Arguments

expand all

Voltage responses of a phased array, specified as a complex-valued matrix or a struct with complex-valued fields. The output depends on whether the array supports polarization or not.

  • If the array elements do not support polarization, the voltage response, RESP, has the dimensions N-by-M-by-L.

    • N (rows) is the number of elements in the array

    • M (columns) is the number of angles specified in ANG

    • L (pages) is the number of frequencies specified in FREQ

    For each array element, the columns of RESP contain the array element responses for the corresponding direction specified in ANG. Each of the L pages of RESP contains the array element responses for the corresponding frequency specified in FREQ.

  • If the array supports polarization, RESP is a MATLAB struct containing two fields, RESP.H and RESP.V. The field, RESP.H, represents the array’s horizontal polarization response, while RESP.V represents the array’s vertical polarization response. Each field has the dimensions N-by-M-by-L.

    • N (rows) is the number of elements in the array

    • M (columns) is the number of angles specified in ANG

    • L (pages) is the number of frequencies specified in FREQ

    For each array element, the columns of RESP.H or RESP.V contain the array element responses for the corresponding direction specified in ANG. Each of the L pages of RESP.H or RESP.V contains the array element responses for the corresponding frequency specified in FREQ.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

beamwidthCompute and display beamwidth of an array
collectPlaneWaveSimulate received plane waves
directivityDirectivity of uniform circular array
getElementNormalNormal vectors for array elements
getElementPositionPositions of array elements
getElementSpacingSpacing between array elements
getNumElementsNumber of elements in array
getTaperArray element tapers
isPolarizationCapablePolarization capability
patternPlot array directivity and patterns
patternAzimuthPlot UCA array directivity or pattern versus azimuth
patternElevationPlot UCA array directivity or pattern versus elevation
perturbationsPerturbations defined on array
perturbedArrayApply perturbations to phased array
perturbedPatternDisplay pattern of perturbed array
sidelobelevelPeak and integrated side-lobe levels
viewArrayView array geometry
stepRun System object algorithm
releaseRelease resources and allow changes to System object property values and input characteristics
resetReset internal states of System object

Examples

collapse all

Open Live Script

Create an 11-element uniform circular array (UCA) having a 1.5 m radius and operating at 500 MHz. The array consists of short-dipole antenna elements. First, display the vertical component of the response at 45 degrees azimuth and 0 degrees elevation. Then plot the azimuth and elevation directivities.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[50e6,1000e6],...
    'AxisDirection','Z');
array = phased.UCA('NumElements',11,'Radius',1.5,'Element',antenna);
fc = 500e6;
ang = [45;0];
resp = array(fc,ang);
disp(resp.V)
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247

Display the azimuth directivity pattern at 500 MHz for azimuth angles between -180 and 180 degrees.

c = physconst('LightSpeed');
pattern(array,fc,[-180:180],0,'Type','directivity','PropagationSpeed',c)

Figure contains an axes object. The hidden axes object contains 3 objects of type line, text. This object represents 500 MHz .

Display the elevation directivity pattern at 500 MHz for elevation angles between -90 and 90 degrees.

pattern(array,fc,[0],[-90:90],'Type','directivity','PropagationSpeed',c)

Figure contains an axes object. The hidden axes object contains 3 objects of type line, text. This object represents 500 MHz .

Algorithms

A UCA is formed from N identical sensor elements equally spaced around a circle of radius R. The circle lies in the xy-plane of the local coordinate system whose origin lies at the center of the circle. The positions of the elements are defined with respect to the local array coordinate system. The circular array lies in the xy-plane of the coordinate system. The normal to the UCA plane lies along the positive z-axis. The elements are oriented so that their main response directions (normals) point radially outward in the xy-plane.

If the number of elements of the array is odd, the middle element lies on the x-axis. If the number of elements is even, the midpoint between the two middle elements lies on the x-axis. For an array of N elements, the azimuth angle of the position of the nth element is given by

φn=(−(N−1)/2+n−1)⋅360/N    n=1,…,N

The azimuth angle is defined as the angle, in the xy-plane, from the x-axis toward the y-axis. The elevation angle is defined as the angle from the xy-plane toward the z-axis. The angular distance between any two adjacent elements is 360/N degrees. Azimuth angle values are in degrees. Elevation angles for all array elements are zero.

References

[1] Brookner, E., ed. Radar Technology. Lexington, MA: LexBook, 1996.

[2] Van Trees, H. Optimum Array Processing. New York: Wiley-Interscience, 2002, pp. 274–304.

Extended Capabilities

Version History

Introduced in R2015a

See Also

| | | | | | | | |

Topics