Main Content

polynomialTrajectory

Piecewise-polynomial trajectory generator

Since R2023a

expand all in page

Description

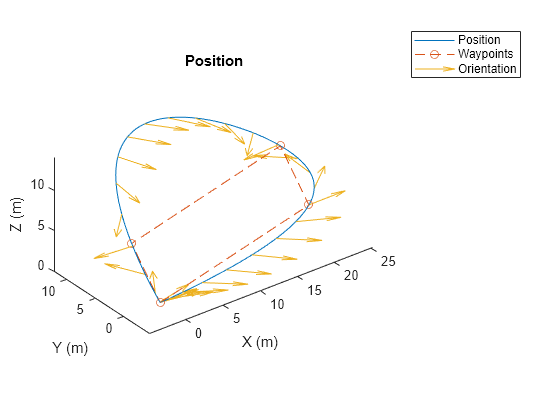
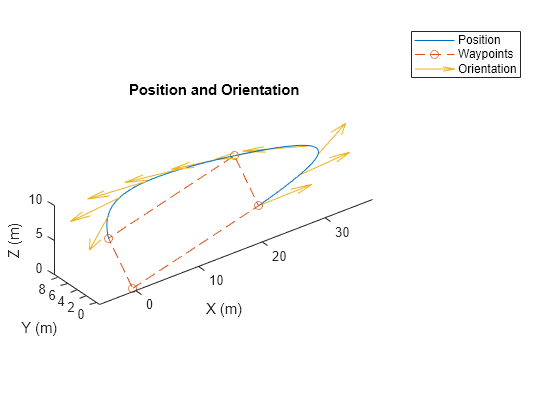
The polynomialTrajectory System object™ generates trajectories using a specified piecewise polynomial.

You can create a piecewise-polynomial structure using trajectory generators like minjerkpolytraj, minsnappolytraj, and cubicpolytraj, as well as any custom trajectory generator. You can then pass the structure to the polynomialTrajectory System object to create a trajectory interface for scenario simulation using the robotScenario object.

To generate a trajectory from a piecewise polynomial:

  1. Create the polynomialTrajectory object and set its properties.

  2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

trajectory = polynomialTrajectory(pp,Name=Value)

Description

trajectory = polynomialTrajectory(pp,Name=Value) returns a System object, trajectory, that generates a trajectory using the piecewise polynomial pp. Specify properties using one or more name-value arguments. Properties that you do not specify retain their default values.

example

Input Arguments

expand all

Piecewise polynomial, specified as a structure that defines the polynomial for each section of the piecewise trajectory.

Data Types: struct

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Sample rate of the trajectory in Hz, specified as a positive scalar.

Tunable: Yes

Data Types: double

Number of samples per output frame, specified as a positive integer.

Data Types: double

Orientation at each waypoint, specified as an N-element quaternion column vector or 3-by-3-by-N array of real numbers. N is the number of waypoints.

Each quaternion must have a norm of 1. Each 3-by-3 rotation matrix must be an orthonormal matrix. Each quaternion or rotation matrix is a frame rotation from the local navigation coordinate system to the current body coordinate system at the corresponding waypoint.

If you do not specify this property, then the object sets yaw to the direction of travel at each waypoint, and pitch and roll are subject to the values of the AutoPitch and AutoBank properties, respectively.

Data Types: double

This property is read-only.

Positions in the navigation coordinate system, in meters, specified as an N-by-3 matrix. The columns of the matrix correspond to the first, second, and third axes, respectively. The rows of the matrix, N, correspond to individual waypoints.

The object infers this value from the piecewise polynomial pp.

Data Types: double

This property is read-only.

Timestamp at each waypoint, in seconds, specified as an N-element column vector. The number of samples, N, is the same as the number of samples (rows) in Waypoints property. The value of each element of the vector must be greater than the value of the previous element.

The object infers this value from the piecewise polynomial pp.

Data Types: double

Align the pitch angle with the direction of motion, specified as a logical 0 (false) or 1 (true). When specified as true, the pitch angle automatically aligns with the direction of motion. If specified as false, the object sets the pitch angle to 0 (level orientation).

Dependencies

To set this property, you must not specify the Orientation property.

Data Types: logical

Align the roll angle to counteract the centripetal force, specified as a logical 0 (false) or 1 (true). When specified as true, the roll angle automatically counteracts the centripetal force. If specified as false, the object sets the roll angle to 0 (flat orientation).

Dependencies

To set this property, you must not specify the Orientation property.

Data Types: logical

Reference frame of the trajectory, specified as "NED" (North-East-Down) or "ENU" (East-North-Up).

Data Types: char | string

This property is read-only.

Velocity in the navigation coordinate system at each waypoint, in meters per second, specified as an N-by-3 matrix. The columns of the matrix correspond to the first, second, and third axes, respectively. The number of samples, N, is the same as the number of samples (rows) in Waypoints property.

The object infers this value from the derivative of the piecewise polynomial pp.

Data Types: double

This property is read-only.

Horizontal direction of travel, in degrees, specified as an N-element real vector. The number of samples, N, is the same as the number of samples (rows) in Waypoints property.

The object infers this value from the derivative of the piecewise polynomial pp.

Data Types: double

This property is read-only.

Groundspeed at each waypoint, in meters per second, specified as an N-element real vector. The number of samples, N, is the same as the number of samples (rows) in Waypoints property.

The object infers this value from the derivative of the piecewise polynomial pp.

Data Types: double

This property is read-only.

Climb Rate at each waypoint, in meters per second, specified as an N-element real vector. The number of samples, N, is the same as the number of samples (rows) in Waypoints property.

The object infers this value from the derivative of the piecewise polynomial pp.

Data Types: double

Usage

Syntax

[position,orientation,velocity,acceleration,angularVelocity] = trajectory()

Description

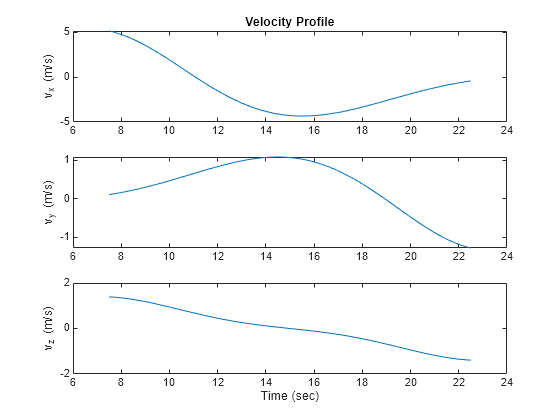
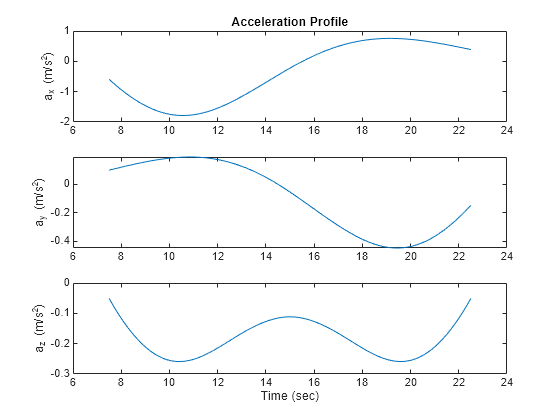
[position,orientation,velocity,acceleration,angularVelocity] = trajectory() outputs a frame of trajectory data based on specified creation arguments and properties. The trajectory returns NaN for positions and orientations outside the range of the time of arrival.

example

Output Arguments

expand all

Position in the local navigation coordinate system, returned as an M-by-3 matrix in meters.

M is specified by the SamplesPerFrame property.

Data Types: double

Orientation in the local navigation coordinate system, returned as an M-element quaternion column vector or a 3-by-3-by-M real array.

Each quaternion or 3-by-3 rotation matrix is a frame rotation from the local navigation coordinate system to the current body coordinate system at the corresponding sample.

M is specified by the SamplesPerFrame property.

Note

If the consecutive roots of the velocity polynomial are within 1e-3 seconds of each other, indicating a sudden change in direction, then the calculated orientation between these roots will be adjusted to maintain continuity.

Data Types: double

Velocity in the local navigation coordinate system, returned as an M-by-3 matrix, in meters per second.

M is specified by the SamplesPerFrame property.

Data Types: double

Acceleration in the local navigation coordinate system, returned as an M-by-3 matrix, in meters per second squared.

M is specified by the SamplesPerFrame property.

Data Types: double

Angular velocity in the local navigation coordinate system, returned as an M-by-3 matrix, in radians per second.

M is specified by the SamplesPerFrame property.

Data Types: double

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

lookupPoseObtain pose information for certain time
waypointInfoGet waypoint information table
stepRun System object algorithm
releaseRelease resources and allow changes to System object property values and input characteristics
cloneCreate duplicate System object
isLockedDetermine if System object is in use
resetReset internal states of System object
isDoneEnd-of-data status

Examples

collapse all

This example uses:

Open Live Script

Use the minjerkpolytraj function to generate the piecewise polynomial and the time samples for the specified waypoints of a trajectory.

waypoints = [0 20 20 0 0; 0 0 5 5 0; 0 5 10 5 0];
timePoints = cumsum([0 10 1.25*pi 10 1.25*pi]);
numSamples = 100;
[~,~,~,~,pp,~,tsamples] = minjerkpolytraj(waypoints,timePoints,numSamples);

Use the polynomialTrajectory System object to generate a trajectory from the piecewise polynomial that a multirotor must follow. Specify the sample rate of the trajectory and the orientation at each waypoint.

eulerAngles = [0 0 0; 0 0 0; 180 0 0; 180 0 0; 0 0 0];
q = quaternion(eulerAngles,"eulerd","ZYX","frame");
traj = polynomialTrajectory(pp,SampleRate=100,Orientation=q);

Inspect the waypoints, times of arrival, and orientation by using waypointInfo.

waypointInfo(traj)
ans=5×3 table
    TimeOfArrival                   Waypoints                      Orientation   
    _____________    ________________________________________    ________________

            0                 0              0              0    {1x1 quaternion}
           10                20              0              5    {1x1 quaternion}
       13.927                20              5             10    {1x1 quaternion}
       23.927                 0              5              5    {1x1 quaternion}
       27.854        6.8449e-14    -1.2168e-13    -6.4837e-14    {1x1 quaternion}

Obtain pose information one buffer frame at a time.

[pos,orient,vel,acc,angvel] = traj();
i = 1;
spf = traj.SamplesPerFrame;
while ~isDone(traj)
    idx = (i+1):(i+spf);
    [pos(idx,:),orient(idx,:), ...
     vel(idx,:),acc(idx,:),angvel(idx,:)] = traj();
    i = i + spf;
end

Get the yaw angle from the orientation.

eulOrientation = quat2eul(orient);
yawAngle = eulOrientation(:,1);

Plot the generated positions and orientations, as well as the specified waypoints.

plot3(pos(:,1),pos(:,2),pos(:,3), ...
      waypoints(1,:),waypoints(2,:),waypoints(3,:),"--o")
hold on
% Plot the yaw using quiver.
quiverIdx = 1:100:length(pos);
quiver3(pos(quiverIdx,1),pos(quiverIdx,2),pos(quiverIdx,3), ...
        cos(yawAngle(quiverIdx)),sin(yawAngle(quiverIdx)), ...
        zeros(numel(quiverIdx),1))
title("Position")
xlabel("X (m)")
ylabel("Y (m)")
zlabel("Z (m)")
legend({"Position","Waypoints","Orientation"})
axis equal
hold off

Figure contains an axes object. The axes object with title Position, xlabel X (m), ylabel Y (m) contains 3 objects of type line, quiver. These objects represent Position, Waypoints, Orientation.

This example uses:

Open Live Script

Use the minsnappolytraj function to generate the piecewise polynomial and the time samples for the specified waypoints of a trajectory.

waypoints = [0 20 20 0 0; 0 0 5 5 0; 0 5 10 5 0];
timePoints = linspace(0,30,5);
numSamples = 100;
[~,~,~,~,~,pp,~,~] = minsnappolytraj(waypoints,timePoints,numSamples);

Use the polynomialTrajectory System object to generate a trajectory from the piecewise polynomial. Specify the sample rate of the trajectory.

traj = polynomialTrajectory(pp,SampleRate=100);

Inspect the waypoints and times of arrival by using waypointInfo.

waypointInfo(traj)
ans=5×2 table
    TimeOfArrival                   Waypoints                
    _____________    ________________________________________

           0                  0              0              0
         7.5                 20              0              5
          15                 20              5             10
        22.5                  0              5              5
          30         6.5364e-14    -2.6699e-12    -2.8679e-12

Obtain the time of arrival between the second and fourth waypoint. Create timestamps to sample the trajectory.

t0 = traj.TimeOfArrival(2);
tf = traj.TimeOfArrival(4);
sampleTimes = linspace(t0,tf,1000);

Obtain the position, orientation, velocity, and acceleration information at the sampled timestamps using the lookupPose object function.

[pos,orient,vel,accel,~] = lookupPose(traj,sampleTimes);

Get the yaw angle from the orientation.

eulOrientation = quat2eul(orient);
yawAngle = eulOrientation(:,1);

Plot the generated positions and orientations, as well as the specified waypoints.

plot3(pos(:,1),pos(:,2),pos(:,3), ...
      waypoints(1,:),waypoints(2,:),waypoints(3,:),"--o")
hold on
% Plot the yaw using quiver.
quiverIdx = 1:100:length(pos);
quiver3(pos(quiverIdx,1),pos(quiverIdx,2),pos(quiverIdx,3), ...
        cos(yawAngle(quiverIdx)),sin(yawAngle(quiverIdx)), ...
        zeros(numel(quiverIdx),1))
title("Position and Orientation")
xlabel("X (m)")
ylabel("Y (m)")
zlabel("Z (m)")
legend({"Position","Waypoints","Orientation"})
axis equal
hold off

Figure contains an axes object. The axes object with title Position and Orientation, xlabel X (m), ylabel Y (m) contains 3 objects of type line, quiver. These objects represent Position, Waypoints, Orientation.

Plot the velocity profiles.

figure
subplot(3,1,1)
plot(sampleTimes,vel(:,1))
title("Velocity Profile")
ylabel("v_x (m/s)")
subplot(3,1,2)
plot(sampleTimes,vel(:,2))
ylabel("v_y (m/s)")
subplot(3,1,3)
plot(sampleTimes,vel(:,3))
ylabel("v_z (m/s)")
xlabel("Time (sec)")

Figure contains 3 axes objects. Axes object 1 with title Velocity Profile, ylabel v_x (m/s) contains an object of type line. Axes object 2 with ylabel v_y (m/s) contains an object of type line. Axes object 3 with xlabel Time (sec), ylabel v_z (m/s) contains an object of type line.

Plot the acceleration profiles.

figure
subplot(3,1,1)
plot(sampleTimes,accel(:,1))
title("Acceleration Profile")
ylabel("a_x (m/s^2)")
subplot(3,1,2)
plot(sampleTimes,accel(:,2))
ylabel("a_y (m/s^2)")
subplot(3,1,3)
plot(sampleTimes,accel(:,3))
ylabel("a_z (m/s^2)")
xlabel("Time (sec)")

Figure contains 3 axes objects. Axes object 1 with title Acceleration Profile, ylabel a_x (m/s^2) contains an object of type line. Axes object 2 with ylabel a_y (m/s^2) contains an object of type line. Axes object 3 with xlabel Time (sec), ylabel a_z (m/s^2) contains an object of type line.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2023a

See Also

Objects

Functions