Main Content

alignsignals

Align two signals by delaying earliest signal

collapse all in page

Syntax

[xa,ya] = alignsignals(x,y)
[xa,ya] = alignsignals(x,y,Name=Value)
[xa,ya,D] = alignsignals(___)

Description

[xa,ya] = alignsignals(x,y) estimates the delay D between the two input signals x and y, and returns the aligned signals xa and ya. The function estimates the delay using cross-correlation.

  • If y is delayed with respect to x, then D is positive and x is delayed by D samples.

  • If y is advanced with respect to x, then D is negative and y is delayed by –D samples.

The input signals need not be exact delayed copies of each other. However, the signals can be accurately aligned only if there is sufficient correlation between them. For more information on estimating covariance and correlation, see [1].

example

[xa,ya] = alignsignals(x,y,Name=Value) specifies options using one or more name-value arguments that include the estimation method and option to truncate the input signals. For example, to estimate the delay based on the location of the largest peak in each signal, set Method to "maxpeak".

example

[xa,ya,D] = alignsignals(___) returns the estimated delay D. You can use any of the previous input syntaxes.

example

Examples

collapse all

Open Live Script

Create two signals, X and Y. X is exactly the same as Y, except X has three leading zeros and one additional following zero. Align the two signals.

X = [0 0 0 1 2 3 0 0];
Y = [1 2 3 0];

[Xa,Ya] = alignsignals(X,Y)
Xa = 1×8

     0     0     0     1     2     3     0     0


Ya = 1×7

     0     0     0     1     2     3     0
Open Live Script

Create two signals, X and Y. Y is exactly the same as X, except Y is delayed by two samples. Align the two signals.

X = [1 2 3];
Y = [0 0 1 2 3];

[Xa,Ya,D] = alignsignals(X,Y)
Xa = 1×5

     0     0     1     2     3


Ya = 1×5

     0     0     1     2     3


D = 
2

Align the signals using a maximum window size of 1.

maxlag = 1;

[Xa,Ya,D] = alignsignals(X,Y,Method="xcorr",MaxLag=maxlag)
Xa = 1×4

     0     1     2     3


Ya = 1×5

     0     0     1     2     3


D = 
1
Open Live Script

Generate two signals that represent bilevel waveforms. The signals are sampled at 50 Hz for 20 seconds. For the first signal, the transition occurs 13 seconds after the start of the measurement. For the second signal, the transition occurs 5 seconds after the start of the measurement. The signals have different amplitudes and are embedded in white Gaussian noise of different variances. Plot the signals.

t = linspace(0,20,1001)';
e1 = 1.4*tanh(t-13)+randn(size(t))/3;
e2 = tanh(3*(t-5))+randn(size(t))/5;

plot(t,e1,t,e2)
xlabel("Seconds")
ylabel("Amplitude")

Figure contains an axes object. The axes object with xlabel Seconds, ylabel Amplitude contains 2 objects of type line.

Align the signals so their transition times coincide. Correlation-based methods cannot align this type of signal adequately.

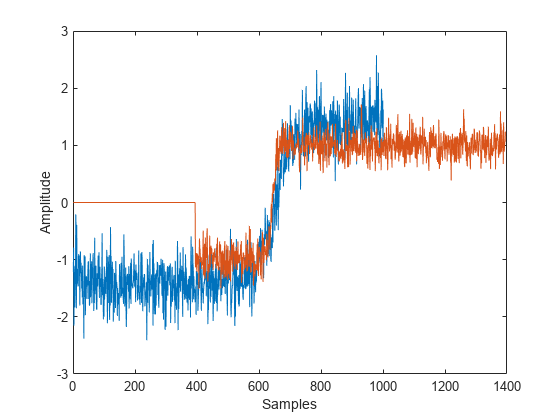
[y1,y2] = alignsignals(e1,e2);

plot(y1)
xlabel("Samples")
ylabel("Amplitude")
hold on
plot(y2)
hold off

Figure contains an axes object. The axes object with xlabel Samples, ylabel Amplitude contains 2 objects of type line.

Align the signals using the risetime method.

[y1,y2] = alignsignals(e1,e2,Method="risetime");

plot(y1)
xlabel("Samples")
ylabel("Amplitude")
hold on
plot(y2)
hold off

Figure contains an axes object. The axes object with xlabel Samples, ylabel Amplitude contains 2 objects of type line.

Open Live Script

Create two signals, X and Y. Y is exactly the same as X, except Y has two leading zeros. Align the two signals and set the truncate option to true. This option preserves the length of X.

X = [1 2 3];
Y = [0 0 1 2 3];

[Xa,Ya,D] = alignsignals(X,Y,Truncate=true)
Xa = 1×3

     0     0     1


Ya = 1×5

     0     0     1     2     3


D = 
2

When the truncate option truncates all the original data of X, the function issues a warning.

Y = [0 0 0 0 1 2 3];

[Xa,Ya,D] = alignsignals(X,Y,Truncate=true)
Warning: All original data in the first input X has been truncated because the length of X is smaller than the estimated delay D. To avoid truncating this data do not use the "truncate" option.

Xa = 1×3

     0     0     0


Ya = 1×7

     0     0     0     0     1     2     3


D = 
4

Input Arguments

collapse all

First input signal, specified as a numeric vector of length Lx.

Example: [1 2 3]

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Complex Number Support: Yes

Second input signal, specified as a numeric vector of length Ly.

Example: [0 0 1 2 3]

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Complex Number Support: Yes

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: alignsignals(X,Y,Method="npeak",PeakNum=4) aligns X and Y based on the location of the fourth peak in each signal.

Method to estimate the delay between signals, specified as "xcorr", "maxpeak", "npeak", or "risetime". You can specify additional name-value arguments based on the specified Method.

  • "xcorr" — Estimate the delay using cross-correlation. If you specify Method as "xcorr", you can also specify MaxLag.

  • "maxpeak" — Estimate the delay using the location of the highest peak in each signal. If you specify Method as "maxpeak", you can optionally specify MinPeakProminence and MinPeakHeight.

  • "npeak" — Estimate the delay using the location of the nth peak in each signal. If you specify Method as "npeak", you can optionally specify PeakNum, MinPeakProminence, and MinPeakHeight.

  • "risetime" — Estimate the delay using the location of the rising edges in each signal. The function uses the specified values for StateLevels to find the rising edges.

Example: Method="npeak",PeakNum=3

Maximum window size used to estimate the delay between signals, specified as an integer scalar. By default, MaxLag is equal to max(Lx,Ly)–1, where Lx is the length of x and Ly is the length of y. If MaxLag is negative, the function uses the absolute value.

This argument applies only when Method is set to "xcorr".

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Peak number used to align the signals, specified as a positive integer. This argument applies only when you specify Method as "npeak".

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Minimum peak prominence used to identify peaks in the signals, specified as a real nonnegative scalar. When you specify MinPeakProminence, the function finds those peaks that have a relative importance of at least the value specified. For more information, see findpeaks and Prominence.

This argument applies only when you specify Method as "npeak" or "maxpeak".

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Minimum peak height used to identify peaks in the signals, specified as a real scalar. When you specify MinPeakHeight, the function finds those peaks with height greater than the specified value. For more information, see findpeaks.

This argument applies only when you specify Method as "npeak" or "maxpeak".

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

State levels, specified as a real-valued two-element row vector. The first element corresponds to the lower state levels of the input signals, and the second element corresponds to the upper state levels of the input signals. If you do not specify StateLevels, the function estimates the state levels of the input waveform by a histogram method. For more information, see risetime.

This argument applies only when you specify Method as "risetime".

Example: Method="risetime",StateLevels=[0.5 2]

Data Types: double

Option to truncate the input signals, specified as a numeric or logical 1 (true) or 0 (false). When you specify Truncate as true, the lengths of xa and ya are equal to the lengths of x and y, respectively.

  • If the estimated delay D is positive, the function prepends D zeros to x and truncates the last D samples of x.

  • If D is negative, the function prepends –D zeros to y and truncates the last D samples of y.

  • If D ≥ Lx, then xa consists of Lx zeros and all samples of x are lost. If –D is ≥ Ly, then ya consists of Ly zeros and all samples of y are lost.

Output Arguments

collapse all

Aligned first signal, returned as a numeric vector that is aligned with the second output argument ya.

  • If input argument x is a row vector, then xa is also a row vector.

  • If input argument x is a column vector, then xa is also a column vector.

If you specify the Truncate as true and the estimated delay D is positive, then xa is equivalent to the input signal x with D zeros prepended to it and its last D samples truncated.

Aligned second signal, returned as a numeric vector that is aligned with the first output argument Xa.

  • If input argument y is a row vector, then ya is also a row vector.

  • If input argument y is a column vector, then ya is also a column vector.

If you specify the Truncate as true and the estimated delay D is negative, then ya is equivalent to the input signal y with –D zeros prepended to it and its last –D samples truncated.

Estimated delay between input signals, returned as an integer. This integer represents the number of samples by which the two input signals x and y are offset.

  • If y is delayed with respect to x, then D is positive and x is delayed by D samples.

  • If y is advanced with respect to x, then D is negative and y is delayed by –D samples.

  • If x and y are already aligned, then D is zero and neither x nor y are delayed.

If you specify a value for input argument MaxLag, then D is less than or equal to MaxLag.

References

[1] Orfanidis, Sophocles J. Optimum Signal Processing. An Introduction. 2nd Ed. Englewood Cliffs, NJ: Prentice-Hall, 1996.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2007a

expand all

See Also

| | | | | |