测量信号的功率
信号的功率是其时域样本的绝对值平方和除以信号长度,或者等效地表示为其 RMS 水平的平方。使用函数 bandpower 只需一步即可估算信号功率。
考虑嵌入在高斯白噪声中的单位啁啾信号,采样率为 1 kHz,采样时间为 1.2 秒。该线性调频的频率在一秒内从初始值 100 Hz 增加到 300 Hz。噪声具有方差 。重置随机数生成器以获得可重现的结果。
N = 1200;
Fs = 1000;
t = (0:N-1)/Fs;
sigma = 0.01;
rng('default')
s = chirp(t,100,1,300)+sigma*randn(size(t));验证 bandpower 给出的功率估计值是否与定义相符。
pRMS = rms(s)^2
pRMS = 0.5003
powbp = bandpower(s,Fs,[0 Fs/2])
powbp = 0.5005
使用 obw 函数来估计包含 99% 信号功率的频带宽度、频带的下限和上限以及频带中的功率。该函数还绘制频谱估计值,并对占用带宽进行注解。
obw(s,Fs);
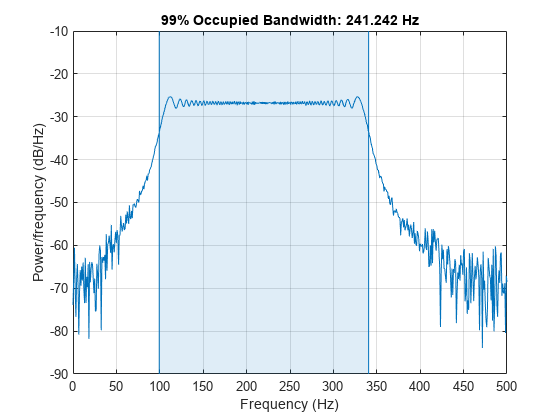
[wd,lo,hi,power] = obw(s,Fs); powtot = power/0.99
powtot = 0.5003
非线性功率放大器的输入为 60 Hz 正弦波,输出为具有三阶失真的含噪信号。信号在 3.6 kHz 下采样 2 秒。
Fs = 3600; t = 0:1/Fs:2-1/Fs; x = sin(2*pi*60*t); y = polyval(ones(1,4),x) + randn(size(x));
由于放大器引入三阶失真,输出信号应该具有:
与输入具有相同频率 (60 Hz) 的基波分量。
两个谐波 - 其频率分量为输入频率的两倍和三倍,即分别为 120 和 180 Hz。
使用 thd 函数来可视化信号频谱。对基波和谐波进行注解。
thd(y,Fs);
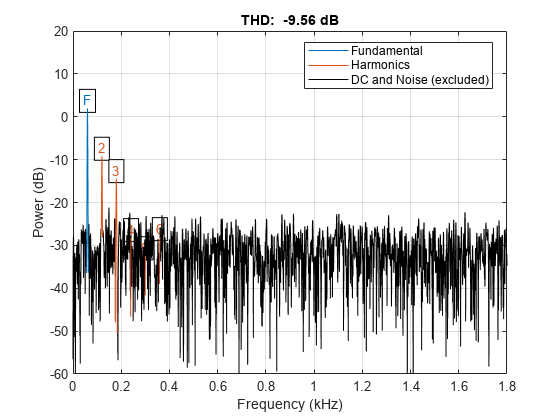
使用 bandpower 确定基波和谐波中存储的功率。以总功率的百分比和分贝表示每个值。将这些值显示为一个表。
pwrTot = bandpower(y,Fs,[0 Fs/2]);
Harmonic = {'Fundamental';'First';'Second'};
Freqs = [60 120 180]';
Power = zeros([3 1]);
for k = 1:3
Power(k) = bandpower(y,Fs,Freqs(k)+[-10 10]);
end
Percent = Power/pwrTot*100;
inDB = pow2db(Power);
T = table(Freqs,Power,Percent,inDB,'RowNames',Harmonic)T=3×4 table
Freqs Power Percent inDB
_____ _______ _______ _______
Fundamental 60 1.5777 31.788 1.9804
First 120 0.13141 2.6476 -8.8137
Second 180 0.04672 0.9413 -13.305
另请参阅
bandpower | pow2db | pwelch | snr