频域分析实践介绍
此示例说明如何执行和解释基本频域信号分析。该示例讨论使用信号的频域表示相对于时域表示的优势,并使用仿真数据和真实数据说明基本概念。该示例回答一些基本问题,例如:FFT 的幅值和相位的含义是什么?我的信号是否为周期性信号?我如何测量功率?此频带中有一个或多个信号吗?
频域分析是信号处理应用中一个至关重要的工具。频域分析广泛用于通信、地质勘测、遥感和图像处理等领域。时域分析显示信号随时间的变化情况,频域分析显示信号能量在频率范围内的分布情况。频域表示还包括必须应用于每个频率分量的相移的有关信息,以便使用所有单独频率分量的组合来恢复原始时间信号。
信号可以通过一对数学运算符在时域和频域之间转换,称为变换。傅里叶变换就是一个示例,它将函数分解为若干(可能无限)个正弦波频率分量之和。各频率分量的“频谱”是信号的频域表示。傅里叶逆变换将频域函数转换回时间函数。MATLAB® 中的 fft 和 ifft 函数允许您分别计算信号的离散傅里叶变换 (DFT) 和此变换的逆变换。
FFT 的幅值和相位信息
信号的频域表示携带每个频率下信号幅值和相位的有关信息。因此,FFT 计算的输出是复数。复数 有实部 和虚部 ,满足 。 的幅值计算为 , 的相位计算为 。使用 MATLAB 函数 abs 和 angle 可以分别得到任意复数的模和相位。
使用一个音频示例来了解信号的幅值和相位携带哪些信息。为此,加载一个包含 15 秒原声吉他音乐的音频文件。音频信号的采样率为 44.1 kHz。
Fs = 44100;
y = audioread("guitartune.wav");使用 fft 观察信号的频率成分。
NFFT = length(y); Y = fft(y,NFFT); F = ((0:1/NFFT:1-1/NFFT)*Fs).';
FFT 的输出是一个复数向量,其中包含关于信号频率成分的信息。幅值显示频率分量相对于其他分量的强度。相位显示所有频率分量按时间对齐的情况。
绘制信号频谱的幅值和相位分量。幅值以对数刻度 (dB) 方便地绘制。使用 unwrap 函数展开相位,以便我们可以看到频率的连续函数。
magnitudeY = abs(Y); % FFT magnitude phaseY = unwrap(angle(Y)); % FFT phase helperFrequencyAnalysisPlot1(F,magnitudeY,phaseY,NFFT)

您可以对频域向量 Y 应用傅里叶逆变换以恢复时间信号。"symmetric" 标志告知 ifft 您正在处理实数值时间信号,因此它会将由于计算中的数值不准确而在逆变换上出现的较小虚部归零。请注意,原始时间信号 y 和恢复后的信号 y1 实际上是相同的(其差值的范数的数量级为 1e-14)。两者之间的微小差值也是由上面提到的数值不准确造成的。播放并聆听傅里叶逆变换信号 y1。
y1 = ifft(Y,NFFT,"symmetric");
norm(y-y1)ans = 3.7900e-14
hplayer = audioplayer(y1,Fs); play(hplayer);
要查看更改信号幅值响应的效果,请直接从 FFT 输出中去除 1 kHz 以上的频率分量(通过使幅值等于零),并通过聆听来了解此操作对音频文件声音的影响。去除信号的高频分量称为低通滤波。
Ylp = Y; Ylp(F>=1000 & F<=Fs-1000) = 0; helperFrequencyAnalysisPlot1(F,abs(Ylp),unwrap(angle(Ylp)), ... NFFT,"Frequency components above 1 kHz have been zeroed")
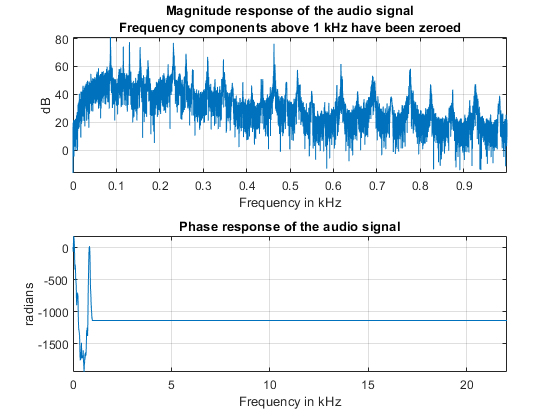
使用 ifft 将滤波后的信号还原为时域表示。
ylp = ifft(Ylp,"symmetric");播放信号。您仍可以听到旋律,但音效就像您捂住了耳朵(捂住耳朵会滤除高频声音)。即使吉他产生 400 到 1 kHz 之间的音符,当您在弦上弹奏音符时,弦也会以基频的倍数振动。这些高频率分量称为谐波,它们使吉他产生特殊音调。当您去除它们时,会使声音显得“不透明”。
hplayer = audioplayer(ylp, Fs); play(hplayer);
信号的相位包含歌曲音符所出现时间的重要信息。为了说明相位对音频信号的重要性,通过获取每个频率分量的幅值来完全去除相位信息。请注意,这样做可以保持幅值响应不变。
% Take the magnitude of each FFT component of the signal Yzp = abs(Y); helperFrequencyAnalysisPlot1(F,abs(Yzp), ... unwrap(angle(Yzp)),NFFT,[],"Phase has been set to zero")

将信号还原为时域表示,播放音频。您根本听不出原声。幅值响应相同,这次没有去掉任何频率分量,但音符的阶完全消失。信号现在由一组正弦波组成,这些正弦波全部在时间等于零处对齐。一般情况下,滤波引起的相位失真会损坏信号,使得无法识别所呈现的信号。
yzp = ifft(Yzp,"symmetric");
hplayer = audioplayer(yzp, Fs);
play(hplayer);寻找信号周期性
信号的频域表示允许您观察信号的几个特征,这些特征或者不容易看到,或者当您在时域中观察信号时根本不可见。例如,当您寻找信号的循环行为时,频域分析变得很有用。
分析办公楼内温度的循环行为
假设存在一组冬季办公楼的温度测量值。测量每 30 分钟进行一次,持续约 16.5 周。查看时间轴缩放至周的时域数据。这些数据会有周期性行为吗?
load officetemp.mat Fs = 1/(60*30); % Sample rate is 1 sample every 30 minutes t = (0:length(temp)-1)/Fs; helperFrequencyAnalysisPlot2(t/(60*60*24*7),temp, ... "Time (weeks)","Temperature (\circF)")
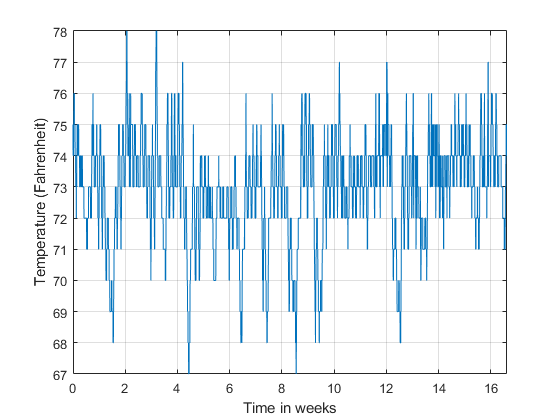
通过观察时域信号,几乎无法知道办公室内温度是否有周期行为。然而,如果我们观察其频域表示,温度的循环行为会变得明显。
获取信号的频域表示。如果您绘制一个频率轴缩放到“周期/周”的 FFT 输出幅值,可以看到有两条频谱线明显大于任何其他频率分量。一条频谱线位于 1 个周期/周,另一条位于 7 个周期/周。这是合理的,因为数据来自以 7 天为日历周期的温控建筑物。第一条频谱线表明,建筑物温度遵循以一周为单位的周期,周末温度较低,一周的工作日温度较高。第二行表示还存在日周期,即白天气温较高,晚上气温较低。
NFFT = length(temp); % Number of FFT points F = (0 : 1/NFFT : 1/2-1/NFFT)*Fs; % Frequency vector TEMP = fft(temp,NFFT); TEMP(1) = 0; % remove the DC component for better visualization helperFrequencyAnalysisPlot2(F*60*60*24*7,abs(TEMP(1:NFFT/2)), ... "Frequency (cycles/week)","Magnitude",[],[],[0 10])
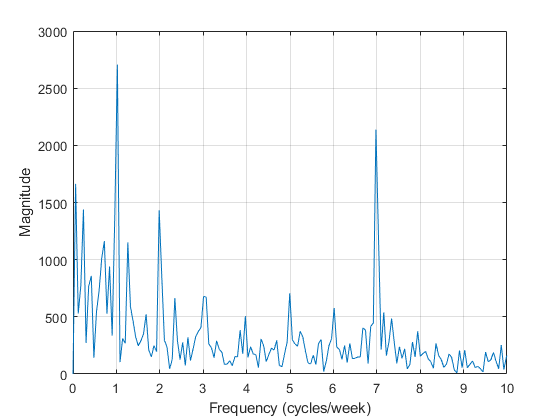
测量功率
periodogram 函数计算信号的 FFT 并对输出进行归一化以获得功率谱密度 (PSD),或获得可从中测量功率的功率谱。PSD 说明时间信号的功率是如何随频率分布的,其单位是瓦特/赫兹。对于 PSD 的每个点,可以通过在定义该点的频率区间内(即在 PSD 的分辨率带宽内)对该点进行积分来计算功率谱。功率谱的单位是瓦特。您可以直接从功率谱中读取功率值,而无需在一个区间内进行积分。请注意,PSD 和功率谱是实数,因此它们不包含任何相位信息。
测量非线性功率放大器的输出的谐波
加载在功率放大器输出端测得的数据,该功率放大器的三阶失真形式为 ,其中 为输出电压, 为输入电压。数据以 3.6 kHz 的采样率进行采集。输入 包含一个具有单位振幅的 60 Hz 正弦波。由于非线性失真的性质,您应预期放大器输出信号包含 DC 分量、60 Hz 分量以及 120 和 180 Hz 的第二个和第三个谐波。
加载放大器输出的 3600 个采样,计算功率谱,并以对数刻度(分贝-瓦特或 dBW)绘制结果。
load ampoutput1.mat Fs = 3600; NFFT = length(y); % Power spectrum is computed when you pass a "power" flag input [P,F] = periodogram(y,[],NFFT,Fs,"power"); helperFrequencyAnalysisPlot2(F,10*log10(P),"Frequency (Hz)", ... "Power spectrum (dBW)",[],[],[-0.5 200])
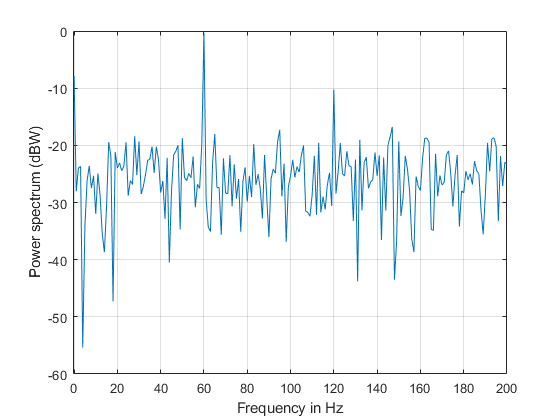
功率谱图显示 DC、60 和 120 Hz 的四个预期峰值中的三个。它还显示其他几个杂散峰值,这些峰值应该是由信号中的噪声引起的。请注意,180 Hz 谐波完全隐藏在噪声中。
测量可见预期峰值的功率:
PdBW = 10*log10(P); power_at_DC_dBW = PdBW(F==0)
power_at_DC_dBW = -7.8873
[peakPowers_dBW, peakFreqIdx] = findpeaks(PdBW,MinPeakHeight=-11); peakFreqs_Hz = F(peakFreqIdx)
peakFreqs_Hz = 2×1
60
120
peakPowers_dBW
peakPowers_dBW = 2×1
-0.3175
-10.2547
改进含噪信号的功率测量值
如上图所示,周期图显示几个与感兴趣信号无关的频率峰值。频谱看起来包含很多噪声。这是因为您只分析了含噪信号的一个短实现。重复几次试验并求平均值可以消除杂散频谱峰值,产生更精确的功率测量值。您可以使用 pwelch 函数来实现这种平均化处理。此函数将接受一个大数据向量,将它分成若干指定长度的小段,计算与段数对应的周期图,然后求其平均值。随着可用段数的增加,pwelch 函数将产生更平滑的功率谱(方差更小),功率值更接近预期值。
加载一个更大的观测值,其中包含放大器输出的 500e3 个点。将用于执行 FFT 的点数保持为 3600,以便对 floor(500e3/3600) = 138 个 FFT 求平均值来获得功率谱。
load ampoutput2.mat SegmentLength = NFFT; % Power spectrum is computed when you pass a "power" flag input [P,F] = pwelch(y,ones(SegmentLength,1),0,NFFT,Fs,"power"); helperFrequencyAnalysisPlot2(F,10*log10(P),"Frequency (Hz)", ... "Power spectrum (dBW)",[],[],[-0.5 200])
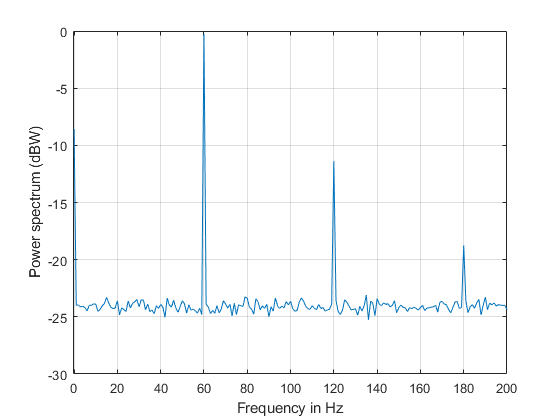
如图所示,pwelch 有效去除了噪声引起的所有杂散频率峰值。隐藏在噪声中的 180 Hz 频谱分量现在可见。求平均值可去除频谱中的方差,从而有效地生成更精确的功率测量值。
测量总平均功率和某频带上的功率
测量时域信号的总平均功率是一项简单而常见的任务。对于放大器输出信号 y,总平均功率在时域中计算如下:
pwr = sum(y.^2)/length(y) % in wattspwr = 8.1697
在频域中,总平均功率计算为信号的所有频率分量的功率之和。pwr1 的值包含信号功率谱中所有可用频率分量的总和。该值与上面使用时域信号计算的 pwr 值一致:
pwr1 = sum(P) % in wattspwr1 = 8.1698
但是,如何测量某频带上的总可用功率?您可以使用 bandpower 函数来计算任一所需频带上的功率。您可以将时域信号直接作为输入传递给此函数,以获得指定频带上的功率。在这种情况下,此函数将使用周期图方法估计功率谱。
计算 50 Hz 到 70 Hz 频带上的功率。结果将包括感兴趣频带上的 60 Hz 功率加上噪声功率:
pwr_band = bandpower(y,Fs,[50 70]);
pwr_band_dBW = 10*log10(pwr_band) % dBWpwr_band_dBW = 0.0341
如果您要控制用于测量某频带功率的功率谱计算,可以将 PSD 向量传递给 bandpower 函数。例如,您可以像以前一样使用 pwelch 函数来计算 PSD,并确保对噪声影响求平均值:
% Power spectral density is computed when you specify the "psd" option [PSD,F] = pwelch(y,ones(SegmentLength,1),0,NFFT,Fs,"psd"); pwr_band1 = bandpower(PSD,F,[50 70],"psd"); pwr_band_dBW1 = 10*log10(pwr_band1) % dBW
pwr_band_dBW1 = 0.0798
寻找频谱分量
一个信号可能包含一个或多个频率分量。观测所有频谱分量的能力取决于您的分析的频率分辨率。功率谱的频率分辨率或分辨率带宽定义为 R = Fs/N,其中 N 是信号观测的长度。只有大于频率分辨率的频率分离的频谱分量才会得到解析。
分析建筑物的地震振动控制系统
主动质量驱动 (AMD) 控制系统用于减少地震时建筑物的振动。主动质量驱动放置在建筑物的顶层,并基于建筑物楼层的位移和加速度测量,由一个控制系统向驱动发送信号,使得质量移动以衰减地表扰动。在地震条件下,加速度测量值记录在三层待测建筑物的第一楼层。测量是在没有主动质量驱动控制系统(开环条件)和有主动控制系统(闭环条件)的情况下分别进行的。
加载加速度数据,并计算第一楼层加速度的功率谱。数据向量的长度为 10e3,采样率为 1 kHz。对长度为 64 个数据点的段使用 pwelch,以获得 floor(10e3/64) = 156 个 FFT 平均值和 Fs/64 = 15.625 Hz 的分辨率带宽。如前所示,求平均值可以降低噪声影响,产生更精确的功率测量值。使用 512 个 FFT 点。使用 NFFT > N 可有效地对频率点进行插值,从而呈现更详细的频谱图(这是通过在时间信号的末尾追加 NFFT-N 个零点并选取零填充向量的 NFFT 点 FFT 来实现的)。
开环和闭环加速度功率谱表明,当控制系统处于活动状态时,加速度功率谱在 4 和 11 dB 之间减小。最大衰减发生在大约 23.44 kHz 处。11 dB 的降幅意味着振动功率按因子 12.6 降低。总功率从 0.1670 瓦特降低到 0.059 瓦特,因子为 2.83。
load quakevibration.mat Fs = 1e3; % sample rate NFFT = 512; % number of FFT points segmentLength = 64; % segment length % open loop acceleration power spectrum [P1_OL,F] = pwelch(gfloor1OL,ones(segmentLength,1),0,NFFT,Fs,"power"); % closed loop acceleration power spectrum P1_CL = pwelch(gfloor1CL,ones(segmentLength,1),0,NFFT,Fs,"power"); helperFrequencyAnalysisPlot2(F,10*log10([(P1_OL) (P1_CL)]),... "Frequency (Hz)","Acceleration Power Spectrum (dB)",... "Resolution bandwidth = 15.625 Hz",["Open" "Closed"]+" loop",[0 100])

您正在分析振动数据并知道振动有循环行为。那么,为什么上面显示的频谱图不包含任何典型循环行为的尖锐频谱线?不显示这些线,是否因为它们无法用包含 64 个点的段长度获得的分辨率来解析?提高频率分辨率,看看是否存在以前无法解析的频谱线。为此,请将 pwelch 函数中使用的数据段长度增加到 512 个点。这会产生 Fs/512 = 1.9531 Hz 的新分辨率。在本例中,FFT 平均值的数目减少到 floor(10e3/512) = 19 个。显然,使用 pwelch 时,平均值的数目和频率分辨率之间存在权衡。保持 FFT 点数等于 512。
NFFT = 512; % number of FFT points segmentLength = 512; % segment length [P1_OL,F] = pwelch(gfloor1OL,ones(segmentLength,1),0,NFFT,Fs,"power"); P1_CL = pwelch(gfloor1CL,ones(segmentLength,1),0,NFFT,Fs,"power"); helperFrequencyAnalysisPlot2(F,10*log10([(P1_OL) (P1_CL)]), ... "Frequency in Hz","Acceleration Power Spectrum in dB", ... "Resolution bandwidth = 1.95 Hz",{"Open loop", "Closed loop"},[0 100])
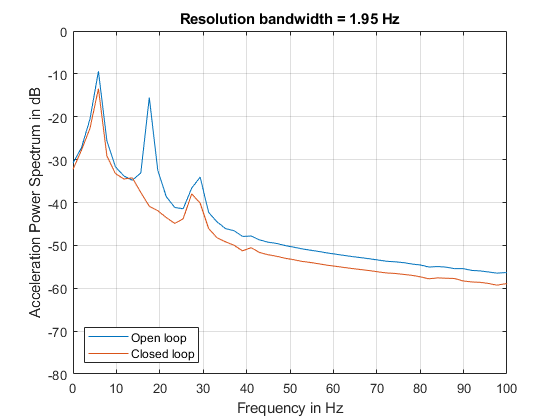
请注意,频率分辨率的提高使您能够观测到开环频谱上的三个峰值和闭环频谱上的两个峰值。这些峰值以前是无法解析的。开环频谱上的峰值之间的间隔约为 11 Hz,小于用长度为 64 的段获得的频率分辨率,但大于用长度为 512 的段获得的分辨率。振动的循环行为现在可见。主振动频率为 5.86 Hz,等间距的频率峰值表明它们是在谐波上相关。虽然已观测到控制系统可降低振动的总功率,但是,更高分辨率频谱表明控制系统的另一个效果是使谐波分量在 17.58 Hz 处出现陷波。因此,控制系统不仅减少振动,还使其更接近正弦波。
请注意,频率分辨率由信号点的数量确定,而不是由 FFT 点的数量确定。增加 FFT 点的数量会对频率数据进行插值,以提供更多频谱细节,但不会提高分辨率。
结论
在此示例中,您学习了如何使用 fft、ifft、periodogram、pwelch 和 bandpower 函数对信号执行频域分析。您已经了解 FFT 的复/实性质,以及频谱的幅值和相位中包含哪些信息。您看到了在分析信号的周期性时使用频域数据的优势。您已经掌握如何计算总功率或含噪信号的特定频带的功率。您已经了解如何通过提高频谱的频率分辨率来观测近距频率分量,并了解频率分辨率和频谱求平均值之间的权衡。
延伸阅读
有关频域分析的详细信息,请参阅频谱分析。
参考资料:J.G. Proakis and D. G. Manolakis, "Digital Signal Processing.Principles, Algorithms, and Applications", Prentice Hall, 1996.
附录
此示例使用以下辅助函数:
另请参阅
fft | periodogram | pspectrum | pwelch