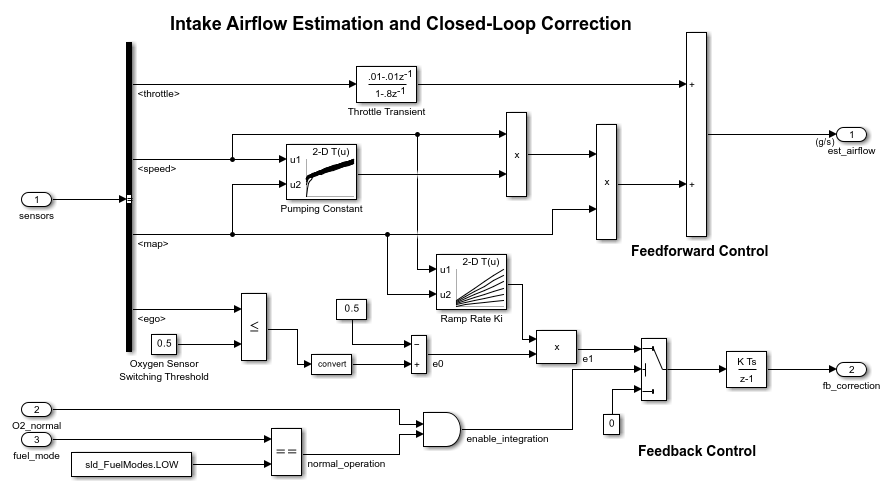
Discrete-Time Integrator

执行信号的离散时间积分或累积

全页展开

库：
Simulink / Commonly Used Blocks
Simulink / Discrete
HDL Coder / Discrete
HDL Coder / HDL Floating Point Operations

描述

使用 Discrete-Time Integrator 模块替代 Integrator 模块来创建纯离散模型。使用 Discrete-Time Integrator 模块，您可以：

在模块对话框上定义初始条件，或作为模块的输入
定义输入增益 (K) 值
输出模块状态
定义积分的上限和下限
使用其他重置输入重置状态

输出方程

对于第一个时间步，模块状态为 n = 0，具有初始输出 y(0) = IC 或初始状态 x(0) = IC，具体取决于初始条件设置参数值。

对于仿真时间为 t(n) 的给定步长 n > 0，Simulink^® 将更新输出 y(n)，如下所示：

前向欧拉方法：

y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n-1)

后向欧拉方法：
```
y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n)
```

梯形法：

y(n) = y(n-1) + K*[t(n)-t(n-1)]*[u(n)+u(n-1)]/2

Simulink 根据模块的采样时间（可以是显式或触发的采样时间）自动选择这些输出方程的状态空间实现。当使用显式采样时间时，对于所有 n > 0 的步长，t(n)-t(n-1) 将减小到采样时间 T。

积分方法和累积方法

此模块可以使用前向欧拉、后向欧拉或梯形法对信号进行积分或累积。假定 u 为输入，y 为输出，x 为状态。对于给定步长 n，Simulink 将更新 y(n) 和 x(n+1)。在积分模式下，T 是模块的采样时间（如果是触发采样时间，则是 delta T）。在累积模式下，T = 1。模块采样时间决定计算输出的时间，而不是输出值。K 是增益值。值根据上限或下限进行剪切。

前向欧拉方法

前向欧拉方法（默认值），也称为正向矩形或左手逼近方法

该软件将 1/s 近似为 T/(z-1)。模块在第 n 个时间步的输出的表达式为：

x(n+1) = x(n) + K*T*u(n)
y(n)   = x(n)

模块按照以下时间步计算输出：

Step 0:          y(0)   = IC (clip if necessary)
                 x(1)   = y(0) + K*T*u(0)

Step 1:          y(1)   = x(1)
                 x(2)   = x(1) + K*T*u(1)

Step n:          y(n)   = x(n)
                 x(n+1) = x(n) + K*T*u(n) (clip if necessary)

使用此方法时，输入端口 1 没有直接馈通。

后向欧拉方法

后向欧拉方法，也称为反向矩形或右手逼近方法

该软件将 1/s 近似为 T*z/(z-1)。模块在第 n 个时间步生成的输出的表达式为：

y(n) = y(n-1) + K*T*u(n).

假设 x(n) = y((n)-1)。模块按照以下时间步计算输出。

如果触发子系统和函数调用子系统的参数初始条件设置设置为“输出”或“自动”：
```
Step 0:          y(0) = IC (clipped if necessary)
                 x(1) = y(0)
```

如果非触发子系统的参数初始条件设置设置为 “”：

Step 0:          x(0)   = IC (clipped if necessary)
                 x(1)   = y(0) = x(0) + K*T*u(0)

Step 1:          y(1)   = x(1) + K*T*u(1)
                 x(2)   = y(1)

Step n:          y(n)   = x(n) + K*T*u(n)
                 x(n+1) = y(n)

使用此方法时，输入端口 1 具有直接馈通。

梯形法

对于此方法，本软件将 1/s 近似为 T/2*(z+1)/(z-1)。

当 T 固定时（等于采样周期），计算输出的表达式为：

x(n) = y(n-1) + K*T/2*u(n-1)
y(n) = x(n) + K*T/2*u(n)

如果触发子系统和函数调用子系统的参数初始条件设置设置为“输出”或“自动”：
```
Step 0:          y(0)   = IC (clipped if necessary)
                 x(1)   = y(0) + K*T/2*u(0)
```

如果非触发子系统的参数初始条件设置设置为 “”：

Step 0:          x(0)   = IC (clipped if necessary)
                 y(0)   = x(0) + K*T/2*u(0)
                 x(1)   = y(0) + K*T/2*u(0)

Step 1:          y(1)   = x(1) + K*T/2*u(1)
                 x(2)   = y(1) + K*T/2*u(1)

Step n:          y(n)   = x(n) + K*T/2*u(n)
                 x(n+1) = y(n) + K*T/2*u(n)

这里，x(n+1) 是下一个输出的最佳估计值。它与状态的不同之处在于，x(n) 不等于 y(n)。

使用此方法时，输入端口 1 具有直接馈通。

当 T 为变量时

当 T 是变量时（例如，从触发时间获得），模块将按照以下时间步计算输出。

如果触发子系统和函数调用子系统的参数初始条件设置设置为“输出”或“自动”：
```
Step 0:          y(0)   = IC (clipped if necessary)
                 x(1)   = y(0)
```

如果非触发子系统的参数初始条件设置设置为 “”：

Step 0:          x(0)   = IC (clipped if necessary)
                 x(1)   = y(0) = x(0) + K*T/2*u(0)

Step 1:          y(1)   = x(1) + K*T/2*(u(1) + u(0))
                 x(2)   = y(1)

Step n:          y(n)   = x(n) + K*T/2*(u(n) + u(n-1))
                 x(n+1) = y(n)

定义初始条件

可以在模块对话框上将初始条件定义为参数，或者从外部信号输入初始条件：

要将初始条件定义为模块参数，请将初始条件来源参数设置为 internal 并在初始条件文本框中输入值。
要从外部源提供初始条件，请将初始条件来源参数设置为 external。模块上出现一个额外的输入端口。

何时使用状态端口

在以下情况下，请使用状态端口而不是输出端口：

当模块输出通过重置端口或初始条件端口馈送回模块，从而产生代数环时。有关示例，请参阅 sldemo_bounce_two_integrators 模型。
当您要从一个条件执行子系统向另一个条件执行子系统传递状态，从而可能导致计时问题时。有关示例，请参阅Building a Clutch Lock-Up Model。

要解决这些问题，您可以通过状态端口而不是输出端口来传递状态。Simulink 在与输出略有不同的时间生成状态，从而避免您的模型出现这些问题。要输出模块状态，请选中显示状态端口复选框。状态端口出现在模块顶部。

限制积分

要使输出在一定的级别内，请选中限制输出复选框，并在对应的文本框中输入范围限制。此操作会使该模块起到限量积分器的作用。当输出达到界限时，积分动作将关闭以防止积分饱和。在仿真期间，您可以更改限制，但不能更改是否限制输出。下表显示了模块如何决定输出。

积分	输出
小于或等于饱和下限且输入为负	保持在饱和下限
介于饱和下限和饱和上限之间	积分
大于或等于饱和上限且输入为正	保持在饱和上限

要生成指示状态正受到限制的信号，请选中显示饱和端口复选框。模块输出端口下方会显示一个新饱和端口。

饱和信号具有以下三个值之一：

1 表示正在应用上限。
0 表示积分不受限制。
-1 表示正在应用下限。

重置状态

模块根据外部信号将其状态重置为指定的初始条件。要使模块重置其状态，请选择外部重置参数选项之一。将出现一个重置端口，指明重置触发器类型。

重置端口具有直接馈通。如果模块输出直接或通过一系列带直接馈通的模块反馈到此端口中，则会产生代数环。要解决此循环，请改为将模块状态端口的输出馈送给重置端口。要访问模块状态，请选中显示状态端口复选框。

重置触发器类型

通过外部重置参数，您可以确定触发重置的重置信号的属性。触发器选项包括：

“上升沿” - 当重置信号具有上升沿时重置状态。例如，下图显示了上升沿重置触发器对后向欧拉积分的影响。
“下降沿” - 当重置信号具有下降沿时重置状态。例如，下图显示了下降沿重置触发器对后向欧拉积分的影响。
“任一沿” - 当重置信号上升或下降时重置状态。例如，下图显示了任一沿重置触发器对后向欧拉积分的影响。
“电平” - 当重置信号非零时重置输出并使输出保持在初始条件。例如，下图显示了电平重置触发器对后向欧拉积分的影响。
“采样电平” - 当重置信号非零时，将输出重置为初始条件。例如，下图显示了采样电平重置触发器对后向欧拉积分的影响。

“采样电平”重置选项需要的计算比较少，因此效率比“电平”重置选项高。
注意
对于 Discrete-Time Integrator 模块，所有触发器检测都基于具有正值的信号。例如，从 -1 变成 0 的信号不是上升沿，但从 0 变成 1 的信号是上升沿。

简化初始化模式下的行为

在配置参数对话框中将“欠定初始化检测”设置为“简化”时，将启用简化初始化模式。如果您使用简化初始化模式，Discrete-Time Integrator 模块的行为将不同于经典初始化模式。新的初始化行为更稳定，并且在以下情况下提供更加一致的行为：

在代数环中
在启用和禁用时
在比较使用触发采样时间和使用显式采样时间（触发模块的速率与显式采样时间的速率相同）的结果时

在简化初始化模式下，Continuous-Time Integrator 模块更容易转换为 Discrete-Time Integrator 模块，因为初始条件对这两个模块的意义相同。

有关经典和简化初始化模式的详细信息，请参阅欠定初始化检测。

“初始条件设置”设置为“输出”时的启用和禁用行为

对于触发子系统和函数调用子系统，当您使用简化初始化模式并将初始条件设置设置为“输出”时，模块的启用和禁用行为将被简化，如下所示。

在禁用时间 t_d：

 y(t_d) = y(t_d-1)

在启用时间 t_e：

如果父级子系统控制端口的启用时的状态设置为“重置”：
```
y(t_e) = IC.
```
如果父级子系统控制端口的启用时的状态设置为“保持”：
```
y(t_e) = y(t_d).
```
下图显示了这种情况。

迭代子系统

使用简化初始化模式时，不能在迭代子系统模块中放置 Discrete-Time Integrator 模块。

在简化初始化模式下，迭代子系统不维护已用时间。因此，如果在迭代子系统模块中放置需要已用时间的 Discrete-Time Integrator 模块，Simulink 将报告错误。

函数调用子系统内的使能子系统中的行为

假设您有一个函数调用子系统，其中包含一个使能子系统，后者又包含一个 Discrete-Time Integrator 模块。将发生以下行为。

积分器方法	函数调用触发端口的采样时间类型	当函数调用子系统在启用后第一次执行时的 `delta T` 值	出现此行为的原因
前向欧拉	触发	`t — tstart`	当函数调用子系统第一次执行时，积分器算法将使用 `tstart` 作为上一个仿真时间。
后向欧拉和梯形	触发	`t — tprevious`	当函数调用子系统第一次执行时，积分器算法将使用 `tprevious` 作为上一个仿真时间。
前向欧拉、后向欧拉和梯形	周期	函数调用生成器的采样时间	在周期性模式下，Discrete-Time Integrator 模块将使用函数调用生成器的采样时间作为 `delta T`。

示例

使用前向欧拉积分方法的离散时间积分

Sldemo_fuelsys 模型在 fuel_rate_control/airflow_calc 子系统中使用 Discrete-Time Integrator 模块。

打开模型

Building a Clutch Lock-Up Model

Use Simulink® to model and simulate a rotating clutch system. Although modeling a clutch system is difficult because of topological changes in the system dynamics during lockup, this example shows how Simulink's enabled subsystems easily handle such problems. We illustrate how to employ important Simulink modeling concepts in the creation of the clutch simulation. Designers can apply these concepts to many models with strong discontinuities and constraints that may change dynamically.

打开模型

弹球的仿真

此示例使用两个弹球 Simulink® 模型来说明对具有 Zeno 行为的混合动态系统进行建模的不同方法。该示例还提供每种方法的优点。

打开模型

端口

输入

全部展开

Port_1 — 输入信号
标量 | 向量 | 矩阵

输入信号，指定为标量、向量或矩阵

IC — 状态的初始条件
标量 | 向量 | 矩阵

状态的初始条件，指定为有限标量、向量或矩阵。

依存关系

要启用此端口，请将初始条件来源设置为“外部”。

输出

全部展开

Port_1 — 输入的离散时间积分或累积
标量 | 向量 | 矩阵

输入信号的离散时间积分或累积，指定为标量、向量或矩阵。

Port_2 — 饱和输出
标量 | 向量 | 矩阵

指示状态何时受限的信号，指定为标量、向量或矩阵。信号具有以下三个值之一：

1 表示正在应用上限。
0 表示积分不受限制。
-1 表示正在应用下限。

依存关系

要启用此端口，请选中显示饱和端口复选框。

数据类型： single | double | int8

Port_3 — 状态输出
标量 | 向量 | 矩阵

模块状态，输出为标量、向量或矩阵。默认情况下，模块将此端口添加到模块图标的顶部。在以下情况下使用状态端口：

模块输出通过重置端口或初始条件端口馈送回模块，从而产生代数环。有关示例，请参阅 sldemo_bounce_two_integrators 模型。
您要从一个条件执行子系统向另一个条件执行子系统传递状态，从而可能导致计时问题。有关示例，请参阅 sldemo_clutch 模型。

有关详细信息，请参阅何时使用状态端口。

依存关系

要启用此端口，请选中显示状态端口复选框。

参数

全部展开

常设

积分器方法 — 累积方法
“`集成:前向欧拉`” （默认） | “`集成:后向欧拉`” | “`集成:梯形`” | “`累加:前向欧拉`” | “`累加:后向欧拉`” | “`累加:梯形`”

指定积分或累积方法。有关详细信息，请参阅输出方程和积分方法和累积方法。

编程用法

模块参数：IntegratorMethod

类型：字符向量

默认值：'Integration: Forward Euler'

增益值 — 与积分器输入相乘的值
`1.0` （默认） | 标量 | 向量

指定与积分器输入相乘的标量、向量或矩阵。增益的每个元素必须为正实数。

指定除 1.0（默认值）之外的值在语义上等效于将 Gain 模块连接到积分器的输入。
有效值包括：
- double(1.0)
- single(1.0)
- [1.1 2.2 3.3 4.4]
- [1.1 2.2; 3.3 4.4]

提示

使用此参数指定输入增益将不需要在生成的代码中执行乘法运算。但是，此参数必须为不可调参数才能实现这一优势。如果您要调整输入增益，请将此参数设置为 1.0，并使用外部 Gain 模块来指定输入增益。

编程用法

模块参数：gainval

类型：字符向量

值：标量 | 向量

默认值：'1.0'

外部重置 — 选择何时将状态重置为初始条件
“`无`” （默认） | “`上升沿`” | “`下降沿`” | “`任一沿`” | “`电平`” | “`采样电平`”

选择将状态重置为其初始条件的触发事件的类型：

“无” - 不将状态重置为初始条件。
“上升沿” - 当重置信号具有上升沿时重置状态。
“下降沿” - 当重置信号具有下降沿时重置状态。
“任一沿” - 当重置信号上升或下降时重置状态。
“电平” - 当重置信号非零时重置输出并使输出保持在初始条件。
“采样电平” - 当重置信号非零时，将输出重置为初始条件。

有关详细信息，请参阅重置状态和重置触发器类型。

编程用法

模块参数：ExternalReset

类型：字符向量

默认值：'none'

初始条件来源 — 选择初始条件的来源
“`内部`” （默认） | “`外部`”

选择初始条件的来源：

“内部” - 从初始条件模块参数获取状态的初始条件。
“外部” - 通过 IC 输入端口从外部模块获取状态的初始条件。

依存关系

选择“内部”将启用初始条件参数。

选择“外部”会禁用初始条件参数并启用 IC 输入端口。

编程用法

模块参数：InitialConditionSource

类型：字符向量、字符串

值：'internal' | 'external'

默认值：'internal'

初始条件 — 状态的初始条件
“`0`” （默认） | 标量 | 向量 | 矩阵

指定模块状态的初始条件。最小值和最大值由输出最小值和输出最大值模块参数限定。

提示

Simulink 软件不允许此模块的初始条件为 inf 或 NaN。

依存关系

要启用此参数，请将初始条件来源设置为“内部”。

编程用法

模块参数：InitialCondition

类型：字符向量、字符串

值：标量 | 向量 | 矩阵

默认值：'0'

初始条件设置 — 选择应用初始条件的位置
“`自动`” （默认） | “`输出`” | “`兼容性`”

选择是否将初始条件参数的值应用于模块状态或模块输出。初始条件也是重置值。

“自动” - 模块选择应用初始条件参数的位置。
- 如果模块位于非触发子系统中，并且积分器方法设置为积分方法，则设置初始条件：
  x(0) = IC
  在重置时：
  x(n) = IC
- 如果模块位于触发子系统或函数调用子系统中，并且积分器方法设置为积分方法，请像选择了“输出”一样设置初始条件。
“输出” - 当模块在触发子系统或函数调用子系统中且积分器方法设置为积分方法时，使用此选项。
设置初始条件：
y(0) = IC
在重置时：
y(n) = IC
“兼容性” - 提供此选项是为了实现向后兼容性。您无法为 Simulink 模型中的 Discrete-Time Integrator 模块选择此选项，但可以为库中的 Discrete-Time Integrator 模块选择此选项。使用此选项维护与在 R2014a 之前创建的 Simulink 模型的兼容性。
在 R2014a 之前，选项“自动”曾为“仅状态(最高效)”。选项“输出”曾为“状态和输出”。具有“兼容性”选项的模块的行为如下所示：
- 如果欠定初始化检测设置为“典型”，则初始条件设置参数的行为与“自动”相同。
- 如果欠定初始化检测设置为“简化”，则初始条件设置参数的行为与“输出”相同。

注意

在 R2014a 之前的 Simulink 版本中，此参数名为将初始条件用作初始值和重置值。

编程用法

模块参数：InitialConditionSetting

类型：字符向量

值：'Auto' | 'Output' | 'Compatibility'

默认值：'Auto'

采样时间(-1 表示继承) — 采样之间的时间间隔
`-1` （默认） | 标量 | 向量

输入时间步之间的离散时间间隔。

默认情况下，模块使用的离散采样时间为 1。要设置不同的采样时间，请输入其他离散值，例如 0.1。

有关详细信息，请参阅指定采样时间。

提示

不要将采样时间指定为 0。此值指定连续采样时间，Discrete-Time Integrator 模块不支持此方式。
不要将采样时间指定为 inf 或 NaN，因为它们不是离散值。
如果您指定 -1 以从上游模块继承采样时间，请验证上游模块使用离散采样时间。例如，Discrete-Time Integrator 模块无法继承采样时间 0。

编程用法

模块参数：SampleTime

类型：字符向量

值：标量 | 向量

默认值：'-1'

限制输出 — 将模块输出值限制在指定范围内
`off` （默认） | `on`

将模块的输出限制为介于饱和下限和饱和上限参数之间的值。

选中此复选框会将模块的输出限制为介于饱和下限和饱和上限参数之间的值。
清除此复选框后，不会限制模块的输出值。

提示

若忽略限制并重置，您可以围绕某个工作点对模型进行线性化。此点可能会导致积分器重置或饱和。

编程用法

模块参数：IgnoreLimit

类型：字符向量

值：'off' | 'on'

默认值：'off'

信号属性

输出最小值 — 范围检查的最小输出值
`[]` （默认） | 标量

Simulink 检查的输出范围的下限值。

Simulink 使用最小值执行下列操作：

某些模块的参数范围检查（请参阅指定模块参数的最小值和最大值）。
仿真范围检查（请参阅指定信号范围和启用仿真范围检查）。
定点数据类型的自动定标。
从模型生成的代码的优化。此优化可删除算法代码，并影响某些仿真模式（如 SIL 或外部模式）的结果。有关详细信息，请参阅Optimize using the specified minimum and maximum values (Embedded Coder)。

注意

输出最小值不会饱和或剪切实际输出信号。请改用 Saturation 模块。

编程用法

模块参数：OutMin

类型：字符向量

值：'[ ]'| 标量

默认值：'[ ]'

输出最大值 — 范围检查的最大输出值
`[]` （默认） | 标量

Simulink 检查的输出范围的上限值。

Simulink 使用最大值执行下列操作：

某些模块的参数范围检查（请参阅指定模块参数的最小值和最大值）。
仿真范围检查（请参阅指定信号范围和启用仿真范围检查）。
定点数据类型的自动定标。
从模型生成的代码的优化。此优化可删除算法代码，并影响某些仿真模式（如 SIL 或外部模式）的结果。有关详细信息，请参阅Optimize using the specified minimum and maximum values (Embedded Coder)。

注意

输出最大值不会饱和或剪切实际输出信号。请改用 Saturation 模块。

编程用法

模块参数：OutMax

类型：字符向量

值：'[ ]'| 标量

默认值：'[ ]'

数据类型 — 输出数据类型
“`Inherit: Inherit via internal rule`” （默认） | “`Inherit: Inherit via back propagation`” | “`double`” | “`single`” | “`int8`” | “`uint8`” | “`int16`” | “`uint16`” | “`int32`” | “`uint32`” | “`int64`” | “`uint64`” | “`fixdt(1,16)`” | “`fixdt(1,16,0)`” | “`fixdt(1,16,2^0,0)`” | “`<数据类型表达式>`”

为输出选择数据类型。该类型可以继承、直接指定或表示为数据类型对象，如 Simulink.NumericType。有关详细信息，请参阅控制信号的数据类型。

当您选择继承的选项时，模块的行为如下所示：

“Inherit: Inherit via internal rule” - Simulink 在考虑嵌入式目标硬件的属性的同时，会选择相应的数据类型来平衡数值准确性、性能和生成的代码大小。如果更改了嵌入式目标的设置，则依内部规则选择的数据类型可能会发生变化。例如，如果该模块将 int8 类型的输入乘以 int16 的增益，并且将 “ASIC/FPGA” 指定为目标硬件类型，则输出数据类型为 sfix24。如果指定“未指定(假定通用 32 位)”（即通用 32 位微处理器）为目标硬件，则输出数据类型为 int32。如果目标微处理器不能提供适应输出范围的字长，Simulink 软件将在诊断查看器中显示错误。
有时软件不能同时满足优化代码效率和保证数值准确性这两个需求。如果内部规则不能满足您对数值准确性或性能的特定需求，请使用下列选项之一：
- 显式指定输出数据类型。
- 使用简单的选项 “Inherit: Same as input”。
- 显式指定默认数据类型（例如 fixdt(1,32,16)），然后使用定点工具为您的模型提供数据类型建议。有关详细信息，请参阅 fxptdlg (Fixed-Point Designer)。
- 要指定您自己的继承规则，请使用 “Inherit: Inherit via back propagation”，然后使用 Data Type Propagation 模块。有关如何使用此模块的示例说明，请参阅 Signal Attributes 模块库中的 Data Type Propagation Examples 模块。
“Inherit: Inherit via back propagation” - 使用驱动模块的数据类型。

编程用法

模块参数：OutDataTypeStr

类型：字符向量

默认值：'Inherit: Inherit via internal rule'

锁定输出数据类型设置以防止被定点工具更改 — 防止定点工具覆盖输出数据类型
`off` （默认） | `on`

选择此参数可防止定点工具覆盖您在模块上指定的输出数据类型。有关详细信息，请参阅Use Lock Output Data Type Setting (Fixed-Point Designer)。

编程用法

模块参数：LockScale

类型：字符向量

值：'off' | 'on'

默认值：'off'

整数舍入模式 — 指定定点运算的舍入模式
“`向下`” （默认） | “`向上`” | “`收敛`” | “`最邻近值`” | “`舍入`” | “`最简`” | “`零`”

选择下列舍入模式之一。

“向上”: 将正值和负值朝正无穷方向舍入。等同于 MATLAB^® ceil 函数。
“收敛”: 将数值舍入到最邻近的可表示值。如果出现结值，则舍入到最邻近的偶数整数。等同于 Fixed-Point Designer™ convergent 函数。
“向下”: 将正值和负值朝负无穷方向舍入。等同于 MATLAB floor 函数。
“最邻近值”: 将数值舍入到最邻近的可表示值。如果出现结值，则朝正无穷方向舍入。等同于 Fixed-Point Designer nearest 函数。
“舍入”: 将数值舍入到最邻近的可表示值。如果出现结值，则将正数朝正无穷方向舍入，将负数朝负无穷方向舍入。等同于 Fixed-Point Designer round 函数。
“最简”: 自动选择是向负无穷大方向舍入还是向零舍入，以生成尽可能有效的舍入代码。
“零”: 将数值向零舍入。等同于 MATLAB fix 函数。

编程用法

模块参数：RndMeth

类型：字符向量

默认值：'Floor'

另请参阅

有关详细信息，请参阅舍入 (Fixed-Point Designer)。

对整数溢出进行饱和处理 — 溢出操作的方法
`off` （默认） | `on`

指定对溢出是进行饱和处理还是绕回处理。

off - 溢出将绕回到数据类型可以表示的合适值。
例如，数字 130 不适合一个有符号的 8 位整数，因此绕回 -126。
on - 将溢出饱和处理为数据类型能够表示的最小值或最大值。
例如，一个有符号的 8 位整数的溢出可以饱和处理为 -128 或 127。

提示

如果您的模型存在可能的溢出，而您希望在生成的代码中进行显式饱和保护，请考虑选中此复选框。
如果您希望优化生成的代码的效率，请考虑清除此复选框。
清除此复选框还可以帮助您避免过度地指定信号超出范围时的处理方式。有关详细信息，请参阅信号范围错误故障排除。
如果选中此复选框，饱和将应用于模块中的每个内部操作，而不仅仅应用于输出或结果。
一般情况下，代码生成进程可以检测到何时不可能发生溢出。在这种情况下，代码生成器不会生成饱和代码。

编程用法

模块参数：SaturateOnIntegerOverflow

类型：字符向量

值：'off' | 'on'

默认值：'off'

状态属性

状态名称 — 模块状态的唯一名称
`''` （默认） | 字母数字字符串

使用此参数为模块状态指定唯一名称。默认值为 ' '。如果此字段为空，则表示未指定任何名称。使用此参数时，请记住以下注意事项：

有效的标识符以字母或下划线字符开始，后跟字母数字或下划线字符。
状态名称仅适用于所选模块。

有关详细信息，请参阅模型接口元素的 C 代码生成配置 (Simulink Coder)。

依存关系

为状态名称指定值并点击应用时，将启用状态名称必须解析为 Simulink 信号对象参数。

编程用法

参数：StateName

类型：字符向量

值：唯一名称

默认值：''

状态名称必须解析为 Simulink 信号对象 — 要求状态名称解析为信号对象的选项
`off` （默认） | `on`

指定是否需要将状态名称解析为信号对象。如果选中此选项，则在指定的状态名称与信号对象的名称不匹配时，软件会在运行时生成错误。

选择此参数将禁用代码生成存储类参数。

依存关系

当您为状态名称参数指定值并将信号解析模型配置参数设置为“无”以外的值时启用。

编程用法

模块参数：StateMustResolveToSignalObject

类型：字符向量

值：'off' | 'on'

默认值：'off'

模块特性

数据类型	`double` \| `fixed point` \| `integer` \| `single`
直接馈通	`是`
多维信号	`否`
可变大小信号	`否`
过零检测	`否`

扩展功能

C/C++ 代码生成
使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。

在触发子系统层次结构中使用时取决于绝对时间。

HDL 代码生成
使用 HDL Coder™ 为 FPGA 和 ASIC 设计生成 Verilog 代码和 VHDL 代码。

HDL Coder™ 提供影响 HDL 实现和综合逻辑的额外配置选项。

HDL 架构

此模块具有一个默认 HDL 架构。

HDL 模块属性

通用
ConstrainedOutputPipeline	通过移动设计中现有延迟的方式来放置在输出端的寄存器的数量。分布式流水线处理不会重新分发这些寄存器。默认值为 `0`。有关详细信息，请参阅ConstrainedOutputPipeline (HDL Coder)。
InputPipeline	要在生成的代码中插入的输入流水线阶段数。分布式流水线处理和受限输出流水线处理可以移动这些寄存器。默认值为 `0`。有关详细信息，请参阅InputPipeline (HDL Coder)。
OutputPipeline	要在生成的代码中插入的输出流水线阶段数。分布式流水线处理和受限输出流水线处理可以移动这些寄存器。默认值为 `0`。有关详细信息，请参阅OutputPipeline (HDL Coder)。

本机浮点
HandleDenormals	指定是否希望 HDL Coder 在设计中插入额外的逻辑来处理非正规数字。非规范数是量级非常小、必须使用包含前导零的尾数才能表示的浮点数。默认值为 “`inherit`”。另请参阅HandleDenormals (HDL Coder)。
LatencyStrategy	指定对于浮点运算符是否将设计中的模块映射到 `inherit`、`Max`、`Min` 或 `Zero`。默认值为 “`inherit`”。另请参阅LatencyStrategy (HDL Coder)。
MantissaMultiplyStrategy	指定在代码生成期间如何实现尾数乘法运算。通过使用不同设置，您可以控制目标 FPGA 设备上 DSP 的使用。默认值为 “`inherit`”。另请参阅MantissaMultiplyStrategy (HDL Coder)。

限制

HDL 代码生成不支持状态端口。清除显示状态端口选项。
HDL 代码生成不支持外部初始条件。将初始条件来源设置为“内部”。
外部重置必须设置为 none、rising 或 falling。
不支持连续采样时间。对模块使用离散采样时间。

Discrete-Time Integrator

描述

输出方程

积分方法和累积方法

定义初始条件

何时使用状态端口

限制积分

重置状态

重置触发器类型

简化初始化模式下的行为

函数调用子系统内的使能子系统中的行为

示例

使用前向欧拉积分方法的离散时间积分

Building a Clutch Lock-Up Model

弹球的仿真

端口

输入

Port_1 — 输入信号 标量 | 向量 | 矩阵

IC — 状态的初始条件 标量 | 向量 | 矩阵

依存关系

输出

Port_1 — 输入的离散时间积分或累积 标量 | 向量 | 矩阵

Port_2 — 饱和输出 标量 | 向量 | 矩阵

依存关系

Port_3 — 状态输出 标量 | 向量 | 矩阵

依存关系

参数

常设

积分器方法 — 累积方法 “集成:前向欧拉” （默认） | “集成:后向欧拉” | “集成:梯形” | “累加:前向欧拉” | “累加:后向欧拉” | “累加:梯形”

编程用法

增益值 — 与积分器输入相乘的值 1.0 （默认） | 标量 | 向量

编程用法

外部重置 — 选择何时将状态重置为初始条件 “无” （默认） | “上升沿” | “下降沿” | “任一沿” | “电平” | “采样电平”

编程用法

初始条件来源 — 选择初始条件的来源 “内部” （默认） | “外部”

依存关系

编程用法

初始条件 — 状态的初始条件 “0” （默认） | 标量 | 向量 | 矩阵

依存关系

编程用法

初始条件设置 — 选择应用初始条件的位置 “自动” （默认） | “输出” | “兼容性”

编程用法

采样时间(-1 表示继承) — 采样之间的时间间隔 -1 （默认） | 标量 | 向量

提示

编程用法

限制输出 — 将模块输出值限制在指定范围内 off （默认） | on

依存关系

编程用法

饱和上限 — 指定积分的上限 inf （默认） | 标量 | 向量 | 矩阵

依存关系

编程用法

饱和下限 — 指定积分的下限 -inf （默认） | 标量 | 向量 | 矩阵

依存关系

编程用法

显示饱和端口 — 启用饱和输出端口 off （默认） | on

依存关系

编程用法

显示状态端口 — 启用状态输出端口 off （默认） | on

依存关系

编程用法

线性化时忽略限制和重置 — 将模块视为不可重置 off （默认） | on

编程用法

信号属性

输出最小值 — 范围检查的最小输出值 [] （默认） | 标量

编程用法

输出最大值 — 范围检查的最大输出值 [] （默认） | 标量

编程用法

编程用法

锁定输出数据类型设置以防止被定点工具更改 — 防止定点工具覆盖输出数据类型 off （默认） | on

编程用法

整数舍入模式 — 指定定点运算的舍入模式 “向下” （默认） | “向上” | “收敛” | “最邻近值” | “舍入” | “最简” | “零”

编程用法

另请参阅

对整数溢出进行饱和处理 — 溢出操作的方法 off （默认） | on

编程用法

状态属性

状态名称 — 模块状态的唯一名称 '' （默认） | 字母数字字符串

依存关系

编程用法

状态名称必须解析为 Simulink 信号对象 — 要求状态名称解析为信号对象的选项 off （默认） | on

Port_1 — 输入信号
标量 | 向量 | 矩阵

IC — 状态的初始条件
标量 | 向量 | 矩阵

Port_1 — 输入的离散时间积分或累积
标量 | 向量 | 矩阵

Port_2 — 饱和输出
标量 | 向量 | 矩阵

Port_3 — 状态输出
标量 | 向量 | 矩阵

积分器方法 — 累积方法
“`集成:前向欧拉`” （默认） | “`集成:后向欧拉`” | “`集成:梯形`” | “`累加:前向欧拉`” | “`累加:后向欧拉`” | “`累加:梯形`”

增益值 — 与积分器输入相乘的值
`1.0` （默认） | 标量 | 向量

外部重置 — 选择何时将状态重置为初始条件
“`无`” （默认） | “`上升沿`” | “`下降沿`” | “`任一沿`” | “`电平`” | “`采样电平`”

初始条件来源 — 选择初始条件的来源
“`内部`” （默认） | “`外部`”

初始条件 — 状态的初始条件
“`0`” （默认） | 标量 | 向量 | 矩阵

初始条件设置 — 选择应用初始条件的位置
“`自动`” （默认） | “`输出`” | “`兼容性`”

采样时间(-1 表示继承) — 采样之间的时间间隔
`-1` （默认） | 标量 | 向量

限制输出 — 将模块输出值限制在指定范围内
`off` （默认） | `on`

饱和上限 — 指定积分的上限
`inf` （默认） | 标量 | 向量 | 矩阵

饱和下限 — 指定积分的下限
`-inf` （默认） | 标量 | 向量 | 矩阵

显示饱和端口 — 启用饱和输出端口
`off` （默认） | `on`

显示状态端口 — 启用状态输出端口
`off` （默认） | `on`

线性化时忽略限制和重置 — 将模块视为不可重置
`off` （默认） | `on`

输出最小值 — 范围检查的最小输出值
`[]` （默认） | 标量

输出最大值 — 范围检查的最大输出值
`[]` （默认） | 标量

锁定输出数据类型设置以防止被定点工具更改 — 防止定点工具覆盖输出数据类型
`off` （默认） | `on`

整数舍入模式 — 指定定点运算的舍入模式
“`向下`” （默认） | “`向上`” | “`收敛`” | “`最邻近值`” | “`舍入`” | “`最简`” | “`零`”

对整数溢出进行饱和处理 — 溢出操作的方法
`off` （默认） | `on`

状态名称 — 模块状态的唯一名称
`''` （默认） | 字母数字字符串

状态名称必须解析为 Simulink 信号对象 — 要求状态名称解析为信号对象的选项
`off` （默认） | `on`

C/C++ 代码生成
使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。

HDL 代码生成
使用 HDL Coder™ 为 FPGA 和 ASIC 设计生成 Verilog 代码和 VHDL 代码。

PLC 代码生成
使用 Simulink® PLC Coder™ 生成结构化文本代码。

定点转换
使用 Fixed-Point Designer™ 设计和仿真定点系统。