Tune Gain-Scheduled Controller for PMSM Model Using Closed-Loop PID Autotuner Block

PMSM Model

The PMSM model is based on the Motor Control Blockset™ mcb_pmsm_foc_sim model. The model includes:

You can examine this model for more details.

In this example, the original model is modified to use a gain-scheduled controller to control the rotational speed of the motor. The gains of the gain-scheduled controller are updated in real-time using dynamic lookup tables. The speed of the motor plant is originally controlled by a single PI controller in the mcb_pmsm_foc_sim Simulink® model.

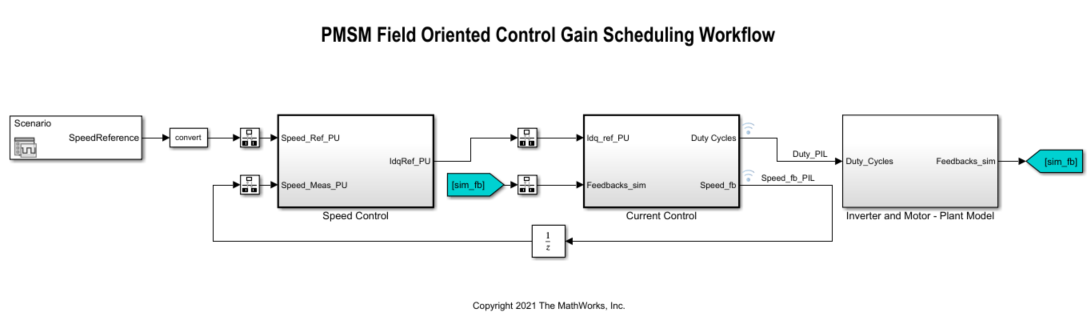
The following sections describe how to modify the mcb_pmsm_foc_sim model to tune and implement a gain-scheduled PI controller. Alternatively, use the preconfigured scd_pid_gs_mcb_pmsm_foc_sim model provided with this example.

Speed Control PI Controller with Gain Scheduling and Closed-Loop PID Autotuner

The Speed Control subsystem consists of a single PI Controller with external inputs for the proportional and integral gains, integrator reset, and integrator initial condition. The PI Controller is set up to use integral gain multiplied by sample time, I*Ts, instead of the integral gain I.

The Closed-Loop PID Autotuner block is located within the Autotuning subsystem. The block outputs the perturbations used to estimate the plant required to tune the controller gains. The Closed-Loop PID Autotuner block tunes gains for P and I but not for I*Ts. To properly update the gains used in the PI Controller, multiply the integral gain by the sample time, as shown in the Closed-Loop PID Autotuner with Gain Updates section of this example.

The Gain Scheduling subsystem contains Lookup Table Dynamic blocks for both the proportional and integral gains. For more details, see the Update PI Controller Gain-Scheduled Gains During Simulation section. The Speed Breakpoints constant block is a vector containing the three breakpoints used in the gain-scheduling lookup tables; this vector is set to [0.2 0.5 0.8] for this example. The Data Store Memory blocks are used to update the gain-scheduled controller gains and pass them to the dynamic lookup tables and then to the controller.

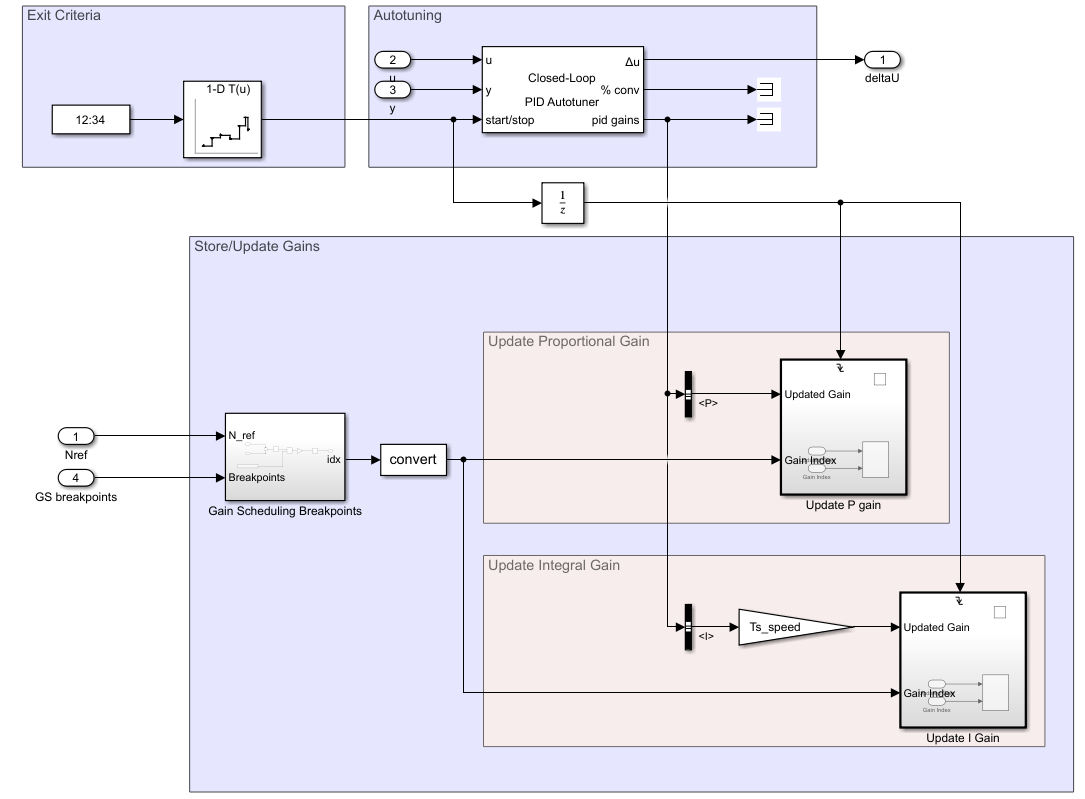
Closed-Loop PID Autotuner with Gain Updates

The Autotuning subsystem contains the Closed-Loop PID Autotuner block, subsystems to update and store the tuned gains, and a subsystem to determine which breakpoint to tune to properly update the scheduled gains.

Closed-Loop PID Autotuner Block Configuration

The design requirements used in this example are in the form of closed-loop step response characteristics.

To tune the PI controller to meet the above design requirements, parameters of the Closed-Loop PID Autotuner block are pre-populated. The Tuning tab has three main tuning settings.

The Experiment tab has three main experiment settings.

These target bandwidth and phase margin are set to values comparable to the default set of gains in the original model. The Closed-Loop PID Autotuner in this example is preconfigured with these settings.

The Data Store Memory blocks used to update the gains are configured to update only a single element at a time to tune individual setpoints and update them in the gain-scheduled controller.

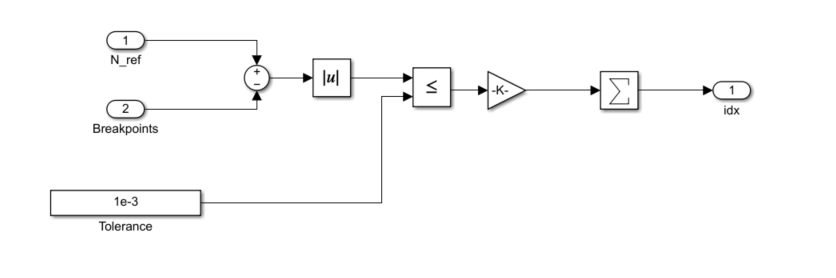
To determine if the current operating point coincides with a breakpoint in the gain-scheduled lookup tables, the current commanded speed reference, N_ref, is compared to the vector of breakpoints used in the gain-scheduled lookup tables. If the current speed is equal to one of the breakpoints and autotuning takes place, then the gains at that breakpoint are updated.

Update PI Controller Gain-Scheduled Gains During Simulation

Typically, the gain-scheduling workflow requires multiple simulations to run the system, tune the gains, update the gains, and then run the system again to demonstrate how to tune gain-scheduled controllers. This example performs all these steps in single a simulation using dynamic lookup tables.

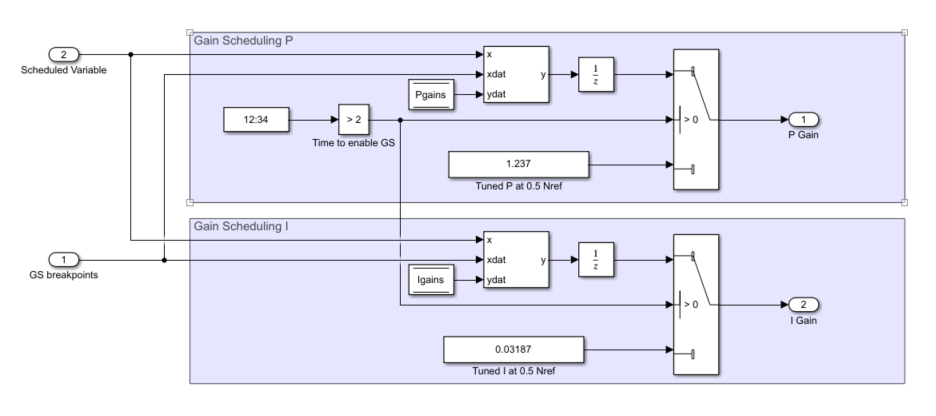
For this example, before 2 seconds, a static set of gains is used. These gains were tuned at the middle breakpoint of the gain-scheduled lookup tables 0.5 N_ref and are used to demonstrate a typical system response if not using gain scheduling. After 2 seconds the gain-scheduled controller gains are used and tuned at three different breakpoints: 0.2, 0.5, and 0.8 N_ref. All breakpoints are tuned using the same settings in the Closed-Loop PID Autotuner block.

Add Nonlinear Load Torque to Inverter and Motor Plant Model

To demonstrate how gain scheduling is used to increase performance in the presence of nonlinearities, the load torque profile contains a nonlinear load torque instead of a static load torque.

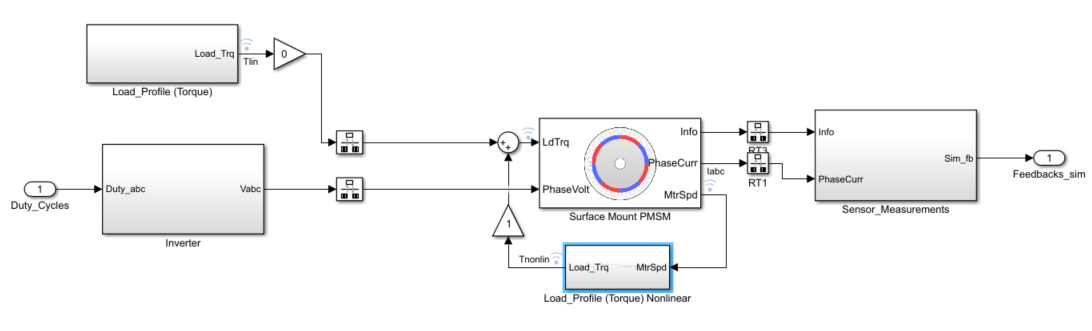
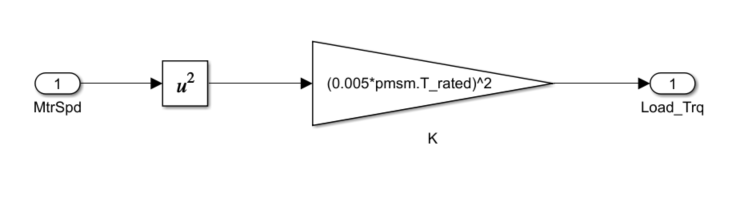
In this example, the nonlinear load is $\tau =\mathit{K}{\omega }_{\mathit{m}}^2$, where $\tau$ is the load torque, $\mathit{K}$ is the load torque constant equal to ${(0.005\times \mathrm{pmsm}.\mathrm{T}\_\mathrm{rated})}^2$, and ${\omega }_{\mathit{m}}$ is the mechanical speed of the motor. From this equation you can see that the load torque and damping in this system increases by mechanical speed squared. This relationship means that at low speed there is little damping, thus requiring smaller controller gains compared to higher speeds where much higher damping is required to achieve the same level of performance.

Tune Gain-Scheduled Controller at Multiple Operating Points

With the model set up, you can now perform tuning at multiple operating points to create a gain-scheduled controller and test the performance of these gains against the gains tuned at 0.5 N_ref in a single simulation. The model is set up to perform a step change at the beginning of the simulation, tune the controller at three operating points (0.2, 0.5, and 0.8 N_ref) and then perform the same step change at the end. This figure shows the profile of the speed reference signal.

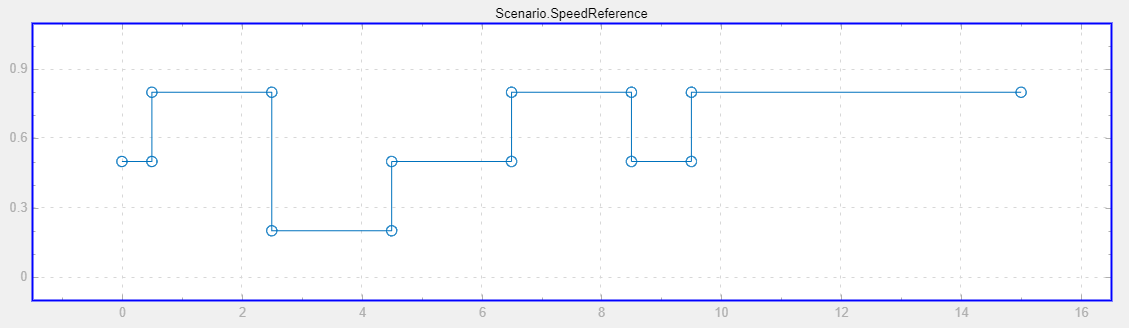
Simulate the model to tune the gains at the three operating points, update the gains in the lookup tables, and test the performance of the tuned gains.

mdl = 'scd_pid_gs_mcb_pmsm_foc_sim';
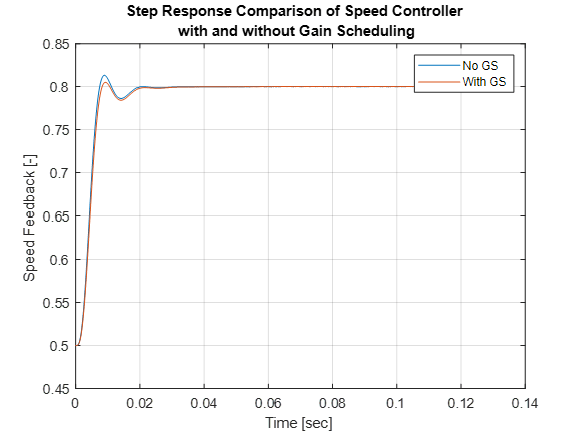
simOut = sim(mdl);

Next, plot a comparison of the initial step response performed with gains tuned at 0.5 N_ref to the response at the end of the simulation performed with gain scheduling.

idx = [0.5 0.75 9.5 9.75]./Ts;
Time_noGS = simOut.tout(idx(1):idx(2))-simOut.tout(idx(1));
SpeedFdbk_noGS = simOut.logsout{2}.Values.Data(idx(1):idx(2));
Time_wGS = simOut.tout(idx(3):idx(4))-simOut.tout(idx(3));
SpeedFdbk_wGS = simOut.logsout{2}.Values.Data(idx(3):idx(4));
figure;
plot(Time_noGS,SpeedFdbk_noGS,Time_wGS,SpeedFdbk_wGS)
legend('No GS', 'With GS','Location','southeast')
grid on
title({'Step Response Comparison of Speed Controller'; 'with and without Gain Scheduling'})
xlabel('Time [sec]')
ylabel('Speed Feedback [-]')

The gain-scheduled controller leads to larger overshoot for a smaller rise time and settling time, compared to a single set of gains tuned at one operating point.

Tuned Gain-Scheduled Controller Performance over Operating Range

You can achieve similar performance for a given step change using a static set of gains obtained at 0.8 N_ref instead of 0.5 N_ref.

However, using this single set of gains to step from 0 to 0.5 N_ref results in poor performance compared to using a gain-scheduled controller.

Gain-scheduling allows for a more consistent and an overall better performance over the operating range compared to just using a static set of gains.

This workflow is useful when you want to tune a gain-scheduled controller using the Closed-Loop PID Autotuner block.

Close the model.

close_system(mdl,0);