synthesizeTabularData

Use existing training data to create a binningTabularSynthesizer object. Then, synthesize data using the synthesizeTabularData object function. Train a model using the existing training data, and then train the same type of model using the synthetic data. Compare the performance of the two models using test data.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Displacement, and so on, as well as the response variable MPG.

load carbig
tbl = table(Acceleration,Cylinders,Displacement,Horsepower, ...
    Model_Year,Origin,MPG,Weight);

Remove rows of tbl where the table has missing values.

tbl = rmmissing(tbl);

Partition the data into training and test sets. Use approximately 60% of the observations for model training and synthesizing new data, and 40% of the observations for model testing. Use cvpartition to partition the data.

rng("default")
cv = cvpartition(size(tbl,1),"Holdout",0.4);
trainTbl = tbl(training(cv),:);
testTbl = tbl(test(cv),:);

Create a binningTabularSynthesizer object by using the trainTbl data set. The binningTabularSynthesizer function uses binning techniques to learn the distribution of the multivariate data set. Use 20 equal-width bins for each continuous variable. Specify the Cylinders and Model_Year variables as discrete numeric variables.

synthesizer = binningTabularSynthesizer(trainTbl, ...
    BinMethod="equal-width",NumBins=20, ...
    DiscreteNumericVariables=["Cylinders","Model_Year"])

synthesizer = 
  binningTabularSynthesizer

               VariableNames: ["Acceleration"    "Cylinders"    "Displacement"    "Horsepower"    "Model_Year"    "Origin"    "MPG"    "Weight"]
        CategoricalVariables: 6
    DiscreteNumericVariables: [2 5]
             BinnedVariables: [1 3 4 7 8]
                   BinMethod: "equal-width"
                     NumBins: [20 20 20 20 20]
                    BinEdges: {[21x1 double]  [21x1 double]  [21x1 double]  [21x1 double]  [21x1 double]}
             NumObservations: 236

synthesizer is a binningTabularSynthesizer object with five binned variables. Each binned variable has the same number of bins.

Synthesize new data by using synthesizer. Specify to generate 1000 observations.

syntheticTbl = synthesizeTabularData(synthesizer,1000);

The synthesizeTabularData object function uses the data distribution information stored in synthesizer to generate syntheticTbl.

To visualize the difference between the existing data and synthetic data, you can use the detectdrift function. The function uses permutation testing to detect drift between trainTbl and syntheticTbl.

dd = detectdrift(trainTbl,syntheticTbl);

dd is a DriftDiagnostics object with plotEmpiricalCDF and plotHistogram object functions for visualization.

For continuous variables, use the plotEmpiricalCDF function to see the difference between the empirical cumulative distribution function (ecdf) of the values in trainTbl and the ecdf of the values in syntheticTbl.

continuousVariable = "Displacement";
plotEmpiricalCDF(dd,Variable=continuousVariable)
legend(["Real Data","Synthetic Data"])

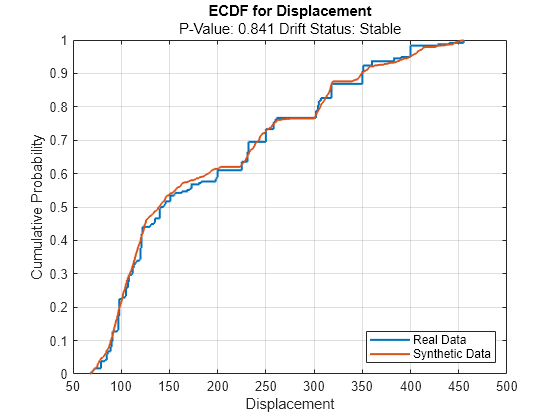
For the Displacement predictor, the ecdf plot for the existing values (in blue) matches the ecdf plot for the synthetic values (in red) fairly well.

For discrete variables, use the plotHistogram function to see the difference between the histogram of the values in trainTbl and the histogram of the values in syntheticTbl.

discreteVariable = "Model_Year";
plotHistogram(dd,Variable=discreteVariable)
legend(["Real Data","Synthetic Data"])

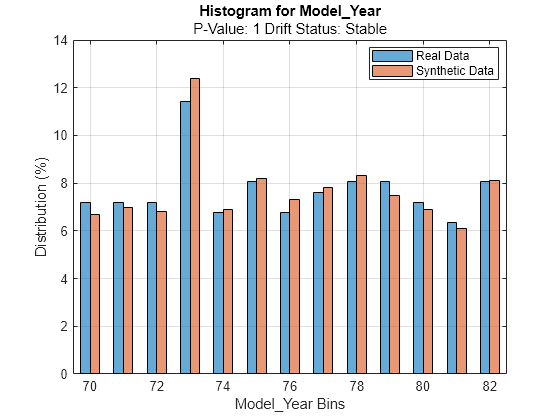
For the Model_Year predictor, the histogram for the existing values (in blue) matches the histogram for the synthetic values (in red) fairly well.

Train a bagged ensemble of trees using the original training data trainTbl. Specify MPG as the response variable. Then, train the same kind of regression model using the synthetic data syntheticTbl.

originalMdl = fitrensemble(trainTbl,"MPG",Method="Bag");
newMdl = fitrensemble(syntheticTbl,"MPG",Method="Bag");

Evaluate the performance of the two models on the test set by computing the test mean squared error (MSE). Smaller MSE values indicate better performance.

originalMSE = loss(originalMdl,testTbl)

originalMSE = 
7.0784

newMSE = loss(newMdl,testTbl)

newMSE = 
6.1031

The model trained on the synthetic data performs slightly better on the test data.

Evaluate data synthesized from an existing data set. Compare the existing and synthetic data sets to determine the similarity between the two multivariate data distributions.

Load the sample file fisheriris.csv, which contains iris data including sepal length, sepal width, petal width, and species type. Read the file into a table, and then convert the Species variable into a categorical variable. Print a summary of the variables in the table.

fisheriris = readtable("fisheriris.csv");
fisheriris.Species = categorical(fisheriris.Species);
summary(fisheriris)

fisheriris: 150x5 table

Variables:

    SepalLength: double
    SepalWidth: double
    PetalLength: double
    PetalWidth: double
    Species: categorical (3 categories)

Statistics for applicable variables:

                   NumMissing       Min          Median         Max           Mean          Std    

    SepalLength        0           4.3000        5.8000        7.9000        5.8433        0.8281  
    SepalWidth         0                2             3        4.4000        3.0573        0.4359  
    PetalLength        0                1        4.3500        6.9000        3.7580        1.7653  
    PetalWidth         0           0.1000        1.3000        2.5000        1.1993        0.7622  
    Species            0                                                                           

The summary display includes statistics for each variable. For example, the sepal length values range from 4.3 to 7.9, with a median of 5.8.

Create 150 new observations from the data in fisheriris. First, create an object by using the binningTabularSynthesizer function. Then, synthesize the data by using the synthesizeTabularData object function. Print a summary of the variables in the new syntheticData data set.

rng(0,"twister") % For reproducibility
synthesizer = binningTabularSynthesizer(fisheriris);
syntheticData = synthesizeTabularData(synthesizer,150);
summary(syntheticData)

syntheticData: 150x5 table

Variables:

    SepalLength: double
    SepalWidth: double
    PetalLength: double
    PetalWidth: double
    Species: categorical (3 categories)

Statistics for applicable variables:

                   NumMissing       Min          Median         Max           Mean          Std    

    SepalLength        0           4.3079        5.7174        7.6399        5.8280        0.8576  
    SepalWidth         0           2.0236        3.0336        4.2866        3.0819        0.4572  
    PetalLength        0           1.0010        4.4453        6.8538        3.6572        1.8192  
    PetalWidth         0           0.1002        1.3502        2.4759        1.1719        0.7597  
    Species            0                                                                           

You can compare the variable statistics for syntheticData to the variable statistics for fisheriris. For example, the sepal length values in the synthetic data set range from approximately 4.3 to 7.6, with a median of 5.7. These statistics are similar to the statistics in the fisheriris data set.

Visually compare the observations in fisheriris and syntheticData by using scatter plots. Each point corresponds to an observation. The point color indicates the species of the corresponding iris.

tiledlayout(1,2)
nexttile
gscatter(fisheriris.SepalLength,fisheriris.PetalLength,fisheriris.Species)
xlabel("Sepal Length")
ylabel("Petal Length")
title("Existing Data")
nexttile
gscatter(syntheticData.SepalLength,syntheticData.PetalLength,syntheticData.Species)
xlabel("Sepal Length")
ylabel("Petal Length")
title("Synthetic Data")

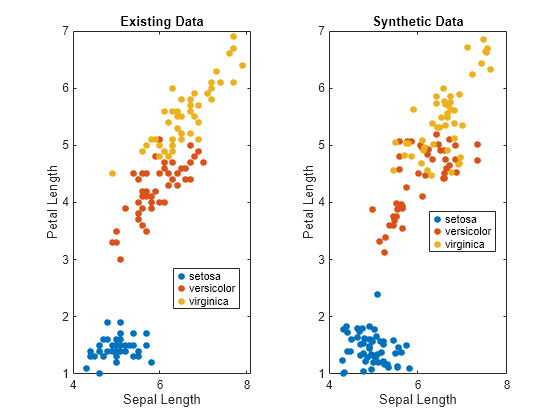
The scatter plots indicate that the existing data set and the synthetic data set have similar characteristics.

Compare the existing and synthetic data sets by using the mmdtest function. The function performs a two-sample hypothesis test for the null hypothesis that the data sets come from the same distribution.

[mmd2,p,h] = mmdtest(fisheriris,syntheticData)

mmd2 = 
0.0020

p = 
0.9600

h = 
0

The returned value of h = 0 indicates that mmdtest fails to reject the null hypothesis that the data sets come from different distributions at the significance level of 5%. As with other hypothesis tests, this result does not guarantee that the null hypothesis is true. That is, the data sets do not necessarily come from the same distribution, but the low mmd2 value (square maximum mean discrepancy) and the high p-value indicate that the distributions of the real and synthetic data sets are similar.