synthesizeTabularData
Description
syntheticX = synthesizeTabularData(X,n)n observations of synthetic data using the existing data
X. The function returns the synthetic data
syntheticX.
syntheticX = synthesizeTabularData(X,n,Name=Value)
Examples
Generate synthetic data using an existing data set in a table. Visually compare the distributions of the existing and synthetic data sets.
Load the sample file fisheriris.csv, which contains iris data including sepal length, sepal width, petal width, and species type. Read the file into a table, and then convert the Species variable into a categorical variable. Display the first eight observations in the table.
fisheriris = readtable("fisheriris.csv");
fisheriris.Species = categorical(fisheriris.Species);
head(fisheriris) SepalLength SepalWidth PetalLength PetalWidth Species
___________ __________ ___________ __________ _______
5.1 3.5 1.4 0.2 setosa
4.9 3 1.4 0.2 setosa
4.7 3.2 1.3 0.2 setosa
4.6 3.1 1.5 0.2 setosa
5 3.6 1.4 0.2 setosa
5.4 3.9 1.7 0.4 setosa
4.6 3.4 1.4 0.3 setosa
5 3.4 1.5 0.2 setosa
Create 1000 new observations from the data in fisheriris by using the synthesizeTabularData function. The function uses a binning technique to learn the distribution of the variables in fisheriris before synthesizing data.
rng("default")
syntheticData = synthesizeTabularData(fisheriris,1000);For each numeric variable, use box plots to visually compare the distribution of the values in fisheriris to the distribution of the values in syntheticData.
numericVariables = ["SepalLength","SepalWidth", ... "PetalLength","PetalWidth"]; boxchart(fisheriris{:,numericVariables}) hold on boxchart(syntheticData{:,numericVariables}) hold off legend(["Real Data","Synthetic Data"]) xticklabels(numericVariables)
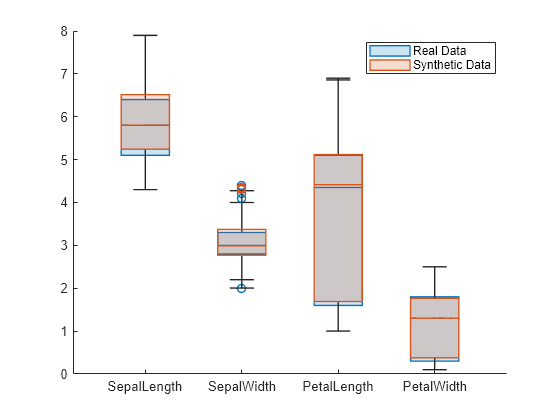
Blue box plots show the distributions of real data, and red box plots show the distributions of synthetic data. For each of the four numeric variables, the real and synthetic data values have similar distributions.
Use histograms to compare the distribution of flower species in fisheriris and syntheticData.
histogram(fisheriris.Species, ... Normalization="probability") hold on histogram(syntheticData.Species, ... Normalization="probability") hold off legend(["Real Data","Synthetic Data"])
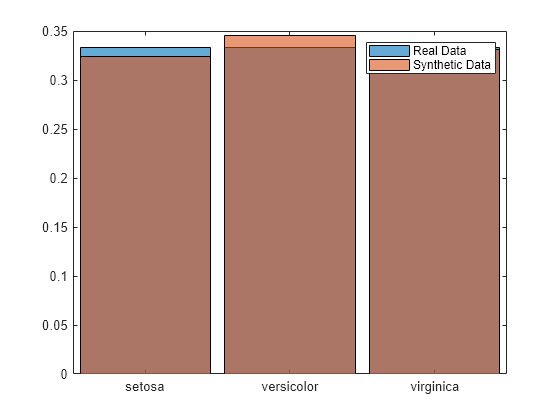
Overall, the distribution of flower species is similar across the two data sets. For example, 32% of the flowers in the synthetic data set are setosa irises, compared to 33% in the real data set.
Synthesize data using existing training data. Train a model using the existing training data, and then train the same type of model using the synthetic data. Compare the performance of the two models using test data.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Displacement, and so on, as well as the response variable MPG.
load carbig tbl = table(Acceleration,Cylinders,Displacement,Horsepower, ... Model_Year,Origin,MPG,Weight);
Remove rows of tbl where the table has missing values.
tbl = rmmissing(tbl);
Partition the data into training and test sets. Use approximately 60% of the observations for model training and synthesizing new data, and 40% of the observations for model testing. Use cvpartition to partition the data.
rng("default") cv = cvpartition(size(tbl,1),"Holdout",0.4); trainTbl = tbl(training(cv),:); testTbl = tbl(test(cv),:);
Synthesize new data by using the trainTbl data set. Specify to generate 1000 observations using 20 equal-width bins for each variable. Specify the Cylinders and Model_Year variables as discrete numeric variables.
syntheticTbl = synthesizeTabularData(trainTbl,1000, ... BinMethod="equal-width",NumBins=20, ... DiscreteNumericVariables=["Cylinders","Model_Year"]);
To visualize the difference between the existing data and synthetic data, you can use the detectdrift function. The function uses permutation testing to detect drift between trainTbl and syntheticTbl.
dd = detectdrift(trainTbl,syntheticTbl);
dd is a DriftDiagnostics object with plotEmpiricalCDF and plotHistogram object functions for visualization.
For continuous variables, use the plotEmpiricalCDF function to see the difference between the empirical cumulative distribution function (ecdf) of the values in trainTbl and the ecdf of the values in syntheticTbl.
continuousVariable ="Acceleration"; plotEmpiricalCDF(dd,Variable=continuousVariable) legend(["Real Data","Synthetic Data"])
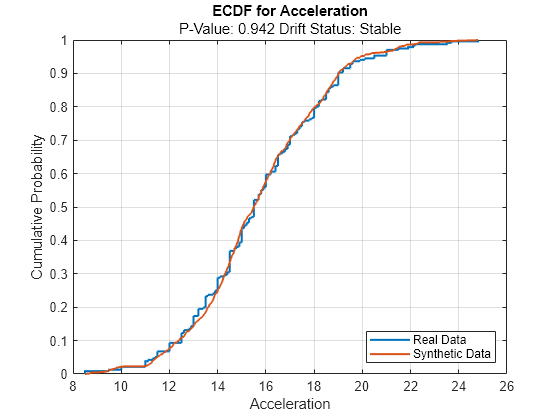
For the Acceleration predictor, the ecdf plot for the existing values (in blue) matches the ecdf plot for the synthetic values (in red) fairly well.
For discrete variables, use the plotHistogram function to see the difference between the histogram of the values in trainTbl and the histogram of the values in syntheticTbl.
discreteVariable ="Cylinders"; plotHistogram(dd,Variable=discreteVariable) legend(["Real Data","Synthetic Data"])
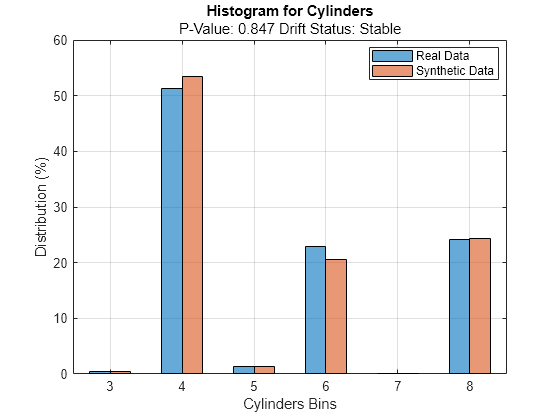
For the Cylinders predictor, the histogram for the existing values (in blue) matches the histogram for the synthetic values (in red) fairly well.
Train a bagged ensemble of trees using the original training data trainTbl. Specify MPG as the response variable. Then, train the same kind of regression model using the synthetic data syntheticTbl.
originalMdl = fitrensemble(trainTbl,"MPG",Method="Bag"); newMdl = fitrensemble(syntheticTbl,"MPG",Method="Bag");
Evaluate the performance of the two models on the test set by computing the test mean squared error (MSE). Smaller MSE values indicate better performance.
originalMSE = loss(originalMdl,testTbl)
originalMSE = 7.0784
newMSE = loss(newMdl,testTbl)
newMSE = 6.1031
The model trained on the synthetic data performs slightly better on the test data.
Evaluate data synthesized from an existing data set. Compare the existing and synthetic data sets to determine distribution similarity.
Load the carsmall data set. The file contains measurements of cars from 1970, 1976, and 1982. Create a table containing the data and display the first eight observations.
load carsmall carData = table(Acceleration,Cylinders,Displacement,Horsepower, ... Mfg,Model,Model_Year,MPG,Origin,Weight); head(carData)
Acceleration Cylinders Displacement Horsepower Mfg Model Model_Year MPG Origin Weight
____________ _________ ____________ __________ _____________ _________________________________ __________ ___ _______ ______
12 8 307 130 chevrolet chevrolet chevelle malibu 70 18 USA 3504
11.5 8 350 165 buick buick skylark 320 70 15 USA 3693
11 8 318 150 plymouth plymouth satellite 70 18 USA 3436
12 8 304 150 amc amc rebel sst 70 16 USA 3433
10.5 8 302 140 ford ford torino 70 17 USA 3449
10 8 429 198 ford ford galaxie 500 70 15 USA 4341
9 8 454 220 chevrolet chevrolet impala 70 14 USA 4354
8.5 8 440 215 plymouth plymouth fury iii 70 14 USA 4312
Generate 100 new observations using the synthesizeTabularData function. Specify the Cylinders and Model_Year variables as discrete numeric variables. Display the first eight observations.
rng("default") syntheticData = synthesizeTabularData(carData,100, ... DiscreteNumericVariables=["Cylinders","Model_Year"]); head(syntheticData)
Acceleration Cylinders Displacement Horsepower Mfg Model Model_Year MPG Origin Weight
____________ _________ ____________ __________ _____________ _________________________________ __________ ______ _______ ______
11.215 8 309.73 137.28 dodge dodge coronet brougham 76 17.3 USA 4038
10.198 8 416.68 215.51 plymouth plymouth fury iii 70 9.5497 USA 4507.2
17.161 6 258.38 77.099 amc amc pacer d/l 76 18.325 USA 3199.8
9.4623 8 426.19 197.3 plymouth plymouth fury iii 70 11.747 USA 4372.1
13.992 4 106.63 91.396 datsun datsun pl510 70 30.56 Japan 1950.7
17.965 6 266.24 78.719 oldsmobile oldsmobile cutlass ciera (diesel) 82 36.416 USA 2832.4
17.028 4 139.02 100.24 chevrolet chevrolet cavalier 2-door 82 36.058 USA 2744.5
15.343 4 118.93 100.22 toyota toyota celica gt 82 26.696 Japan 2600.5
Visualize the synthetic and existing data sets. Create a DriftDiagnostics object using the detectdrift function. The object has the plotEmpiricalCDF and plotHistogram object functions you can use to visualize continuous and discrete variables.
dd = detectdrift(carData,syntheticData);
Use plotEmpiricalCDF to visualize the empirical cumulative distribution function (ECDF) of the values in carData and syntheticData.
continuousVariable ="Acceleration"; plotEmpiricalCDF(dd,Variable=continuousVariable) legend(["Real Data","Synthetic Data"])
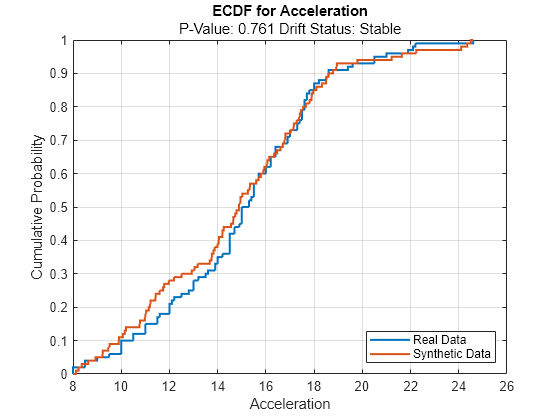
For the variable Acceleration, the ECDF of the existing data (in blue) and the ECDF of the synthetic data (in red) appear to be similar.
Use plotHistogram to visualize the distribution of values for discrete variables in carData and syntheticData.
discreteVariable ="Cylinders"; plotHistogram(dd,Variable=discreteVariable) legend(["Real Data","Synthetic Data"])
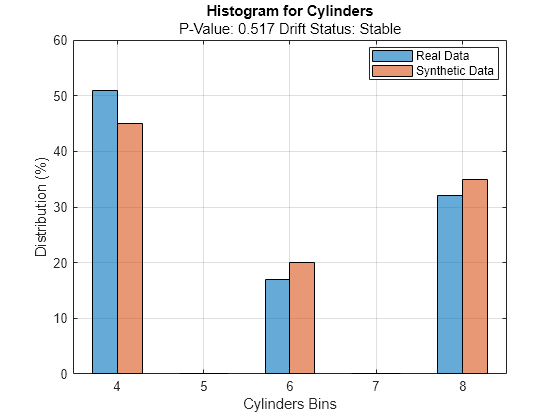
For the variable Cylinders, the distribution of data between the bins for the existing data (in blue) and the synthetic data (in red) appear similar.
Compare the synthetic and existing data sets using the mmdtest function. The function performs a two-sample hypothesis test for the null hypothesis that the samples come from the same distribution.
[mmd,p,h] = mmdtest(carData,syntheticData)
mmd = 0.0078
p = 0.8860
h = 0
The returned value of h = 0 indicates that mmdtest fails to reject the null hypothesis that the samples come from different distributions at the 5% significance level. As with other hypothesis tests, this result does not guarantee that the null hypothesis is true. That is, the samples do not necessarily come from the same distribution, but the low MMD value and high p-value indicate that the distributions of the real and synthetic data sets are similar.
Input Arguments
Existing data set, specified as a numeric matrix or a table. Rows of
X correspond to observations, and columns of
X correspond to variables. Multicolumn variables and cell arrays
other than cell arrays of character vectors are not allowed in
X.
Data Types: single | double | table
Number of synthetic data observations to generate, specified as a positive integer scalar.
Example: 100
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: synthesizeTabularData(X,100,BinMethod="equiprobable",NumBins=10)
specifies to use 10 equiprobable bins for each variable in X to generate
100 synthetic observations.
Binning algorithm, specified as one of the values in this table.
| Value | Description |
|---|---|
"auto" |
|
"equal-width" | Equal-width binning, where you must specify the number of bins using the
NumBins name-value argument |
"equiprobable" | Equiprobable binning, where you must specify the number of bins using the
NumBins name-value argument |
"dagostino-stephens" or "ds" | Equiprobable binning with ceil(2*m^(2/5)) bins, where m
is the number of observations in the existing data |
"freedman-diaconis" or "fd" | Equal-width binning, where each bin for variable
|
"scott" | Equal-width binning, where each bin for variable
|
"scott-multivariate" | Equal-width binning, where each bin for variable
|
"terrell-iqr" | Equal-width binning, where each bin for variable
|
"terrell-scott" or "ts" | Equal-width binning with ceil((2*m)^(1/3)) bins, where
m is the number of observations in the
existing data |
"terrell-std" | Equal-width binning, where each bin for variable
|
Example: BinMethod="scott"
Data Types: char | string
Number of bins to use for continuous variables, specified as a positive integer scalar or vector.
If
NumBinsis a scalar, then the function uses the same number of bins for each continuous variable.If
NumBinsis a vector, then the function usesNumBins(k)number of bins for continuous variablek.
Specify this value only when BinMethod is
"equal-width" or "equiprobable".
Example: NumBins=[10 25 10 15]
Data Types: single | double
Variable names, specified as a string array or a cell array of character vectors.
You can specify VariableNames to choose which variables to use in
table X. That is, synthesizeTabularData uses only the
variables in VariableNames to generate synthetic data.
Xmust be a table, andVariableNamesmust be a subset ofX.Properties.VariableNames.By default,
VariableNamescontains the names of all variables.
Example: VariableNames=["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
List of the categorical variables, specified as one of the values in this table.
| Value | Description |
|---|---|
| Positive integer vector | Each entry in the vector is an index
value indicating that the corresponding variable
is categorical. The index values are between 1 and
v, where v
is the number of variables listed in
|
| Logical vector | A |
| String array or cell array of character vectors | Each element in the array is the name of a
categorical variable. The names must match the
entries in
VariableNames. |
"all" | All variables are categorical. |
By default, if the variables are in a numeric matrix, the software assumes all the variables
are continuous. If the variables are in a table, the software assumes they are
categorical if they are logical vectors, categorical vectors, character
arrays, string arrays, or cell arrays of character vectors. To identify any other
variables as categorical, specify them by using the
CategoricalVariables name-value argument.
Do not specify discrete numeric variables as categorical variables. Use the
DiscreteNumericVariables name-value argument instead.
Example: CategoricalVariables="all"
Data Types: single | double | logical | string | cell
List of the discrete numeric variables, specified as one of the values in this table.
| Value | Description |
|---|---|
| Positive integer vector | Each entry in the vector is an index value indicating that
the corresponding variable is a discrete numeric variable. The
index values are between 1 and v, where
v is the number of variables listed in
|
| Logical vector | A |
| String array or cell array of character vectors | Each element in the array is the name of a discrete numeric
variable. The names must match the entries in
VariableNames. |
"all" | All variables are discrete numeric variables. |
You cannot specify categorical variables as discrete numeric variables.
Example: DiscreteNumericVariables=[2 5]
Data Types: single | double | logical | string | cell
Options for computing in parallel and setting random streams, specified as a
structure. Create the Options structure using statset. This table lists the option fields and their
values.
| Field Name | Value | Default |
|---|---|---|
UseParallel | Set this value to true to run computations in
parallel. | false |
UseSubstreams | Set this value to To compute
reproducibly, set | false |
Streams | Specify this value as a RandStream object or
cell array of such objects. Use a single object except when the
UseParallel value is true
and the UseSubstreams value is
false. In that case, use a cell array that
has the same size as the parallel pool. | If you do not specify Streams, then
synthesizeTabularData uses the default stream or
streams. |
Note
You need Parallel Computing Toolbox™ to run computations in parallel.
Example: Options=statset(UseParallel=true,UseSubstreams=true,Streams=RandStream("mlfg6331_64"))
Data Types: struct
Output Arguments
Synthetic data set, returned as a numeric matrix or a table.
syntheticX and X have the same data
type.
Algorithms
The synthesizeTabularData function estimates the distribution of the multivariate
data set X by performing these steps:
Bin each continuous variable using equiprobable or equal-width binning, as specified by the
BinMethodandNumBinsname-value arguments.Encode the continuous variables using the bin indices.
One-hot encode all binned and discrete variables.
Compute the probability of each unique row in the encoded data set.
The synthesizeTabularData function uses the computed probabilities to
generate synthetic data.
The process for estimating the multivariate data distribution includes computing the
probability of each unique row in the one-hot encoded data set (after binning continuous
variables). The synthesizeTabularData function uses this estimated
multivariate data distribution to generate synthetic observations. The function performs
these steps:
Use the previously computed probabilities to sample with replacement
nrows from the unique rows in the encoded data set.Decode the sampled data to obtain the bin indices (for continuous variables) and categories (for discrete variables).
For the binned variables, uniformly sample from within the bin edges to obtain continuous values. If you use equiprobable binning (
BinMethod) and the extreme bin widths are greater than 1.5 times the median of the nonextreme bin widths, then the function samples from the cumulative distribution function (cdf) in the extreme bins.
Alternative Functionality
Instead of calling the synthesizeTabularData function to generate
synthetic data directly, you can first create a binningTabularSynthesizer object using an existing data set, and then call the
synthesizeTabularData object function to synthesize data using the object. By
creating an object, you can easily generate synthetic data multiple times without having to
relearn characteristics of the existing data set.
Extended Capabilities
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2024b
See Also
binningTabularSynthesizer | synthesizeTabularData | mmdtest | knntest | detectdrift | plotEmpiricalCDF | plotHistogram
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)