mmdtest

Two-sample multivariate hypothesis test using maximum mean discrepancy (MMD)

Since R2024b

collapse all in page

Syntax

mmdval = mmdtest(X,Y)

mmdval = mmdtest(X,Y,Name=Value)

[mmdval,p] = mmdtest(___)

[mmdval,p,h] = mmdtest(___)

Description

mmdval = mmdtest(X,Y) returns the square maximum mean discrepancy (MMD) for the data sets X and Y. The square MMD is a measurement of distance used to quantify the difference between two distributions.

example

mmdval = mmdtest(X,Y,Name=Value) returns the square MMD with additional options specified by one or more name-value arguments. For example, you can limit which variables to include in the calculation and specify options for parallel computing.

example

[mmdval,p] = mmdtest(___) also returns the p-value p of the hypothesis test, using any of the input argument combinations in the previous syntaxes. The function computes the value of p using permutation testing to generate a distribution.

example

[mmdval,p,h] = mmdtest(___) also returns the test decision h for the null hypothesis that the multivariate data sets X and Y come from the same distribution. The alternative hypothesis is that X and Y come from different distributions. The result h is 1 if the test rejects the null hypothesis at the 5% significance level, and 0 otherwise.

example

Examples

collapse all

Calculate and Compare Square MMD Values

Open Live Script

Calculate and compare the square MMD values for cars manufactured in the USA, Japan, and Germany to determine which two countries have the most similar distribution of automobile measurements between 1970 and 1982.

Load the carbig data set, which contains measurements of cars manufactured from 1970 to 1982. Create a table from this data and display the first eight rows.

load carbig
carData = table(Acceleration,Cylinders,Displacement, ...
    Horsepower,Model_Year,Origin,MPG,Weight);
head(carData)

    Acceleration    Cylinders    Displacement    Horsepower    Model_Year    Origin     MPG    Weight
    ____________    _________    ____________    __________    __________    _______    ___    ______

          12            8            307            130            70        USA        18      3504 
        11.5            8            350            165            70        USA        15      3693 
          11            8            318            150            70        USA        18      3436 
          12            8            304            150            70        USA        16      3433 
        10.5            8            302            140            70        USA        17      3449 
          10            8            429            198            70        USA        15      4341 
           9            8            454            220            70        USA        14      4354 
         8.5            8            440            215            70        USA        14      4312

The Origin data is stored in a character array. Convert this data to strings for easier manipulation.

carData.Origin = strtrim(string(carData.Origin));

Create separate tables containing all the data for cars manufactured in the USA, Japan, and Germany.

carUSA = carData(carData.Origin=="USA",:);
carJapan = carData(carData.Origin=="Japan",:);
carGermany = carData(carData.Origin=="Germany",:);

Create a vector containing the names of all the variables except Origin. Because the data sets have different values for Origin, omit this variable from the square MMD value computation.

variableNames = ["Acceleration","Cylinders","Displacement", ...
    "Horsepower","Model_Year","MPG","Weight"];

Use the mmdtest function to calculate the square MMD value for the USA and Japan data sets, the USA and Germany data sets, and the Germany and Japan data sets. Specify which variables to include in the computation by using the VariableNames name-value argument.

mmdUSAJapan = mmdtest(carUSA,carJapan,VariableNames=variableNames);
mmdUSAGermany = mmdtest(carUSA,carGermany,VariableNames=variableNames);
mmdGermanyJapan = mmdtest(carGermany,carJapan,VariableNames=variableNames);

Display the three square MMD values. Recall that the square MMD is a measurement of distance used to quantify the difference between two distributions. In general, a smaller square MMD value indicates greater similarity between two data sets.

countries = ["USA-Japan","USA-Germany","Germany-Japan"];
mmdValues = [mmdUSAJapan,mmdUSAGermany,mmdGermanyJapan];
bar(countries,mmdValues)
ylabel("Square MMD")

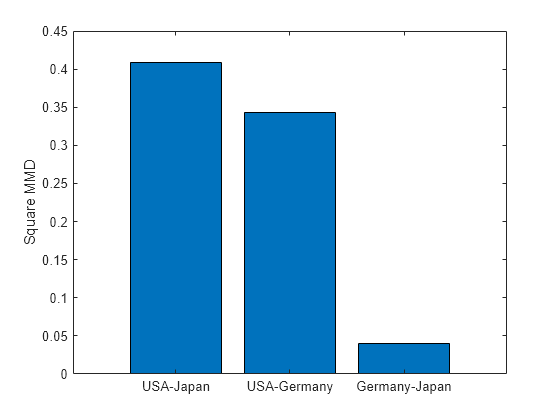
Figure contains an axes object. The axes object with ylabel Square MMD contains an object of type bar.

The bar graph shows that Germany and Japan have the smallest square MMD value. This result indicates that Germany and Japan have the most similar distribution of car measurements between 1970 and 1982.

Test Two Samples for Distribution Similarity

Open Live Script

Perform a two-sample hypothesis test using the square MMD value to determine if two iris species have the same distribution of sepal and petal dimensions. The null hypothesis of the test is that the data sets for the two iris species come from the same distribution. The alternative hypothesis is that the data sets come from different distributions.

First, perform a hypothesis test on two samples of iris data with even numbers of each iris species. Load the fisheriris data set into a table and display the first eight rows.

fisheriris = readtable("fisheriris.csv");
head(fisheriris)

    SepalLength    SepalWidth    PetalLength    PetalWidth     Species  
    ___________    __________    ___________    __________    __________

        5.1           3.5            1.4           0.2        {'setosa'}
        4.9             3            1.4           0.2        {'setosa'}
        4.7           3.2            1.3           0.2        {'setosa'}
        4.6           3.1            1.5           0.2        {'setosa'}
          5           3.6            1.4           0.2        {'setosa'}
        5.4           3.9            1.7           0.4        {'setosa'}
        4.6           3.4            1.4           0.3        {'setosa'}
          5           3.4            1.5           0.2        {'setosa'}

Split the data set into two samples with even distribution of the species.

cv = cvpartition(fisheriris.Species,"Holdout",0.5);
sample1 = fisheriris(cv.training,:);
sample2 = fisheriris(cv.test,:);

Perform a hypothesis test at the 1% significance level using the mmdtest function.

[mmdValue,p,h] = mmdtest(sample1,sample2,Alpha=0.01)

mmdValue = 
0.0048

p = 
0.9200

h = 
0

The returned test decision of h = 0 indicates that mmdtest fails to reject the null hypothesis that the samples come from the same distribution at the 1% significance level. The low value of mmdValue suggests that the samples have similar distributions.

Next, perform a hypothesis test to compare the distribution of petal and sepal data for the setosa and virginica iris species. Create separate tables containing the data for the setosa and virginica iris species.

setosa = fisheriris(string(fisheriris.Species)=="setosa",:);
virginica = fisheriris(string(fisheriris.Species)=="virginica",:);

Store the sepal and petal data for each species in a numeric matrix.

setosaData = setosa{:,1:end-1};
virginicaData = virginica{:,1:end-1};

Perform a hypothesis test at the 1% significance level using the mmdtest function.

[mmdValue,p,h] = mmdtest(setosaData,virginicaData,Alpha=0.01)

mmdValue = 
0.5257

p = 
0

h = 
1

The returned test decision of h = 1 indicates that mmdtest rejects the null hypothesis that the samples come from the same distribution at the 1% significance level. This result indicates that the setosa and virginica iris species have different distributions of sepal and petal data.

Evaluate Synthetic Tabular Data

Open Live Script

Evaluate data synthesized from an existing data set. Compare the existing and synthetic data sets to determine distribution similarity.

Load the carsmall data set. The file contains measurements of cars from 1970, 1976, and 1982. Create a table containing the data and display the first eight observations.

load carsmall
carData = table(Acceleration,Cylinders,Displacement,Horsepower, ...
    Mfg,Model,Model_Year,MPG,Origin,Weight);
head(carData)

    Acceleration    Cylinders    Displacement    Horsepower         Mfg                       Model                  Model_Year    MPG    Origin     Weight
    ____________    _________    ____________    __________    _____________    _________________________________    __________    ___    _______    ______

          12            8            307            130        chevrolet        chevrolet chevelle malibu                70        18     USA         3504 
        11.5            8            350            165        buick            buick skylark 320                        70        15     USA         3693 
          11            8            318            150        plymouth         plymouth satellite                       70        18     USA         3436 
          12            8            304            150        amc              amc rebel sst                            70        16     USA         3433 
        10.5            8            302            140        ford             ford torino                              70        17     USA         3449 
          10            8            429            198        ford             ford galaxie 500                         70        15     USA         4341 
           9            8            454            220        chevrolet        chevrolet impala                         70        14     USA         4354 
         8.5            8            440            215        plymouth         plymouth fury iii                        70        14     USA         4312

Generate 100 new observations using the synthesizeTabularData function. Specify the Cylinders and Model_Year variables as discrete numeric variables. Display the first eight observations.

rng("default")
syntheticData = synthesizeTabularData(carData,100, ...
    DiscreteNumericVariables=["Cylinders","Model_Year"]);
head(syntheticData)

    Acceleration    Cylinders    Displacement    Horsepower         Mfg                       Model                  Model_Year     MPG      Origin     Weight
    ____________    _________    ____________    __________    _____________    _________________________________    __________    ______    _______    ______

       11.215           8           309.73         137.28      dodge            dodge coronet brougham                   76          17.3    USA          4038
       10.198           8           416.68         215.51      plymouth         plymouth fury iii                        70        9.5497    USA        4507.2
       17.161           6           258.38         77.099      amc              amc pacer d/l                            76        18.325    USA        3199.8
       9.4623           8           426.19          197.3      plymouth         plymouth fury iii                        70        11.747    USA        4372.1
       13.992           4           106.63         91.396      datsun           datsun pl510                             70         30.56    Japan      1950.7
       17.965           6           266.24         78.719      oldsmobile       oldsmobile cutlass ciera (diesel)        82        36.416    USA        2832.4
       17.028           4           139.02         100.24      chevrolet        chevrolet cavalier 2-door                82        36.058    USA        2744.5
       15.343           4           118.93         100.22      toyota           toyota celica gt                         82        26.696    Japan      2600.5

Visualize the synthetic and existing data sets. Create a DriftDiagnostics object using the detectdrift function. The object has the plotEmpiricalCDF and plotHistogram object functions you can use to visualize continuous and discrete variables.

dd = detectdrift(carData,syntheticData);

Use plotEmpiricalCDF to visualize the empirical cumulative distribution function (ECDF) of the values in carData and syntheticData.

continuousVariable = "Acceleration";
plotEmpiricalCDF(dd,Variable=continuousVariable)
legend(["Real Data","Synthetic Data"])

Figure contains an axes object. The axes object with title ECDF for Acceleration, xlabel Acceleration, ylabel Cumulative Probability contains 2 objects of type stair. These objects represent Real Data, Synthetic Data.

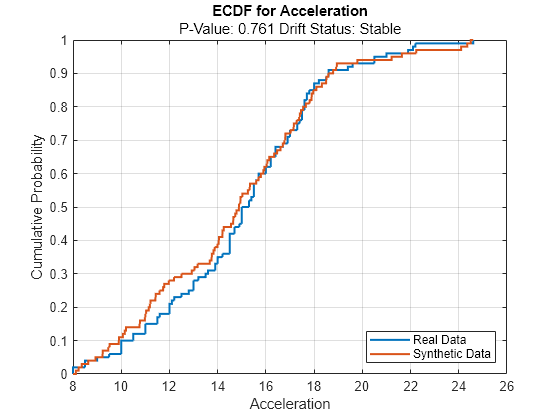
For the variable Acceleration, the ECDF of the existing data (in blue) and the ECDF of the synthetic data (in red) appear to be similar.

Use plotHistogram to visualize the distribution of values for discrete variables in carData and syntheticData.

discreteVariable = "Cylinders";
plotHistogram(dd,Variable=discreteVariable)
legend(["Real Data","Synthetic Data"])

Figure contains an axes object. The axes object with title Histogram for Cylinders, xlabel Cylinders Bins, ylabel Distribution (%) contains 2 objects of type bar. These objects represent Real Data, Synthetic Data.

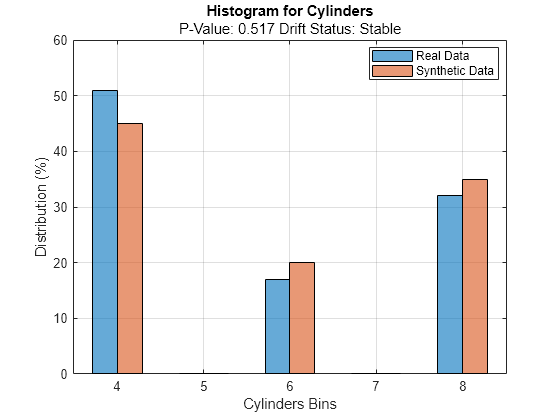
For the variable Cylinders, the distribution of data between the bins for the existing data (in blue) and the synthetic data (in red) appear similar.

Compare the synthetic and existing data sets using the mmdtest function. The function performs a two-sample hypothesis test for the null hypothesis that the samples come from the same distribution.

[mmd,p,h] = mmdtest(carData,syntheticData)

mmd = 
0.0078

p = 
0.8860

h = 
0

The returned value of h = 0 indicates that mmdtest fails to reject the null hypothesis that the samples come from different distributions at the 5% significance level. As with other hypothesis tests, this result does not guarantee that the null hypothesis is true. That is, the samples do not necessarily come from the same distribution, but the low MMD value and high p-value indicate that the distributions of the real and synthetic data sets are similar.

Input Arguments

collapse all

`X` — Sample data
numeric matrix | table

Sample data, specified as a numeric matrix or a table. The rows of X correspond to observations, and the columns correspond to variables. mmdtest ignores observations with missing data.

If X and Y are numeric matrices, they must have the same number of variables, but can have different numbers of observations.
If X and Y are tables, they must have the same variable names, or the variable names of one must be a subset of the other. X and Y can have different numbers of observations.

mmdtest uses X as reference data to normalize continuous variables and establish a set of categories for categorical variables. When a categorical variable is in both X and Y, the variable in Y cannot contain categories that are not in X.

Data Types: single | double | table

`Y` — Sample data
numeric matrix | table

Sample data, specified as a numeric matrix or table. The rows of Y correspond to observations, and the columns correspond to variables. mmdtest ignores observations with missing data.

If X and Y are numeric matrices, they must have the same number of variables, but can have different numbers of observations.
If X and Y are tables, they must have the same variable names, or the variable names of one must be a subset of the other. X and Y can have different numbers of observations.

Data Types: single | double | table

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: mmdtest(X,Y,Alpha=0.01,NumPermutations=500) specifies a test that performs 500 permutations at the 1% significance level.

`Alpha` — Significance level
`0.05` (default) | scalar value in the range (0,1)

Significance level of the hypothesis test, specified as a scalar value in the range (0,1).

Example: Alpha=0.01

Data Types: single | double

`NumPermutations` — Number of permutations
`1000` (default) | positive integer scalar

Number of permutations used to construct the probability distribution for permutation testing, specified as a positive integer scalar. Permutation testing is performed only when you specify the output p or h.

For more information, see Permutation Testing.

Example: NumPermutations=100

Data Types: single | double

`VariableNames` — Variables to include in MMD computation
character vector | string array | cell array of character vectors

Variables to include in the MMD computation, specified as a character vector, string array, or cell array of character vectors. Because matrices do not have named variables, this argument applies only when X and Y are tables.

VariableNames must be a subset of the variables shared by X and Y.
By default, VariableNames contains all the variables shared by X and Y.

Example: VariableNames=["Name","Age","Score"]

Data Types: char | string | cell

`CategoricalVariables` — Variables to treat as categorical
`"all"` | vector of numeric indices | logical vector | string array | cell array of character vectors

Variables to treat as categorical, specified as one of the values in this table.

Value	Description
`"all"`	All variables contain categorical values.
Vector of numeric indices	Each vector element corresponds to the index of a variable, indicating that the variable contains categorical values.
Logical vector	A logical vector the same length as `VariableNames`. A value of `true` indicates that the corresponding variable contains categorical values.
String array or cell array of character vectors	An array containing the names of variables with categorical values. The array elements must be names found in `VariableNames`.

If X and Y are numeric matrices, then CategoricalVariables cannot be a string array or cell array of character vectors. By default, mmdtest assumes all variables in numeric matrices are continuous, and treats table columns of character arrays or string scalars as categorical variables.

Example: CategoricalVariables="all"

`Options` — Options for computing in parallel and setting random streams
structure

Options for computing in parallel and setting random streams, specified as a structure. Create the Options structure using statset. This table lists the option fields and their values.

Field Name Value Default

UseParallel Set this value to true to run computations in parallel. false

Field Name	Value	Default
`UseParallel`	Set this value to `true` to run computations in parallel.	`false`
`UseSubstreams`	Set this value to `true` to run computations in a reproducible manner. To compute reproducibly, set `Streams` to a type that allows substreams: `"mlfg6331_64"` or `"mrg32k3a"`.	`false`
`Streams`	Specify this value as a `RandStream` object or cell array of such objects. Use a single object except when the `UseParallel` value is `true` and the `UseSubstreams` value is `false`. In that case, use a cell array that has the same size as the parallel pool.	If you do not specify `Streams`, then `mmdtest` uses the default stream or streams.

UseSubstreams

Set this value to true to run computations in a reproducible manner.

To compute reproducibly, set Streams to a type that allows substreams: "mlfg6331_64" or "mrg32k3a".

false

Streams Specify this value as a RandStream object or cell array of such objects. Use a single object except when the UseParallel value is true and the UseSubstreams value is false. In that case, use a cell array that has the same size as the parallel pool. If you do not specify Streams, then mmdtest uses the default stream or streams.

Note

You need Parallel Computing Toolbox™ to run computations in parallel.

Example: Options=statset(UseParallel=true,UseSubstreams=true,Streams=RandStream("mlfg6331_64"))

Data Types: struct

Output Arguments

collapse all

`mmdval` — Square MMD value
nonnegative scalar

Square MMD value, returned as a nonnegative scalar. mmdval is the square of the maximum mean discrepancy metric for the data sets X and Y.

`p` — p-value
scalar value in the range [0,1]

p-value of the test, returned as a scalar value in the range [0,1]. p is the probability of observing a test statistic that is as extreme as, or more extreme than, the observed value under the null hypothesis. A small value of p indicates that the null hypothesis might not be valid.

`h` — Hypothesis test result
`1` | `0`

Hypothesis test result, returned as 1 or 0.

A value of 1 indicates the rejection of the null hypothesis at the Alpha significance level.
A value of 0 indicates a failure to reject the null hypothesis at the Alpha significance level.

More About

collapse all

Maximum Mean Discrepancy Metric

The maximum mean discrepancy (MMD) is a measure of distance between the feature means of two independent multivariate distributions. The MMD uses a kernel function to compute the inner product in reproducing kernel Hilbert space (RKHS), and subtracts the cumulative similarity between the data sets from the cumulative similarity of the data sets with themselves. Higher MMD values indicate that the data sets are from different distributions. An MMD value of 0 indicates that the distributions are identical.

mmdtest calculates the biased empirical estimate of the square MMD. For two data sets X and Y with m and n observations, the square MMD is

${MMD}^{2} = \frac{1}{m^{2}} \sum_{i, j = 1}^{m} k (x_{i}, x_{j}) - \frac{2}{m n} \sum_{i, j = 1}^{m, n} k (x_{i}, y_{j}) + \frac{1}{n^{2}} \sum_{i, j = 1}^{n} k (y_{i}, y_{j})$

where k represents the kernel function.

Permutation Testing

Permutation testing is a type of nonparametric hypothesis test that uses resampling to create a distribution of all possible test statistic values. The sample test statistic is compared to the generated distribution to calculate the p-value and test decision. The number of permutations used to generate this distribution is specified by the NumPermutations name-value argument of the mmdtest function. Performing more permutations creates a more robust distribution, but is more computationally intensive.

References

[1] Gretton, Arthur, Karsten M. Borgwardt, Malte J. Rasch, Bernhard Schölkopf, and Alexander Smola. “A Kernel Two-Sample Test.” Journal of Machine Learning Research 13, no. 25 (2012): 723–73. http://jmlr.org/papers/v13/gretton12a.html.

Version History

Introduced in R2024b

mmdtest

Syntax

Description

Examples

Calculate and Compare Square MMD Values

Test Two Samples for Distribution Similarity

Evaluate Synthetic Tabular Data

Input Arguments

X — Sample data numeric matrix | table

Y — Sample data numeric matrix | table

Name-Value Arguments

Alpha — Significance level 0.05 (default) | scalar value in the range (0,1)

NumPermutations — Number of permutations 1000 (default) | positive integer scalar

VariableNames — Variables to include in MMD computation character vector | string array | cell array of character vectors

CategoricalVariables — Variables to treat as categorical "all" | vector of numeric indices | logical vector | string array | cell array of character vectors

Options — Options for computing in parallel and setting random streams structure

Output Arguments

mmdval — Square MMD value nonnegative scalar

p — p-value scalar value in the range [0,1]

h — Hypothesis test result 1 | 0

More About

Maximum Mean Discrepancy Metric

Permutation Testing

References

Version History

See Also

`X` — Sample data
numeric matrix | table

`Y` — Sample data
numeric matrix | table

`Alpha` — Significance level
`0.05` (default) | scalar value in the range (0,1)

`NumPermutations` — Number of permutations
`1000` (default) | positive integer scalar

`VariableNames` — Variables to include in MMD computation
character vector | string array | cell array of character vectors

`CategoricalVariables` — Variables to treat as categorical
`"all"` | vector of numeric indices | logical vector | string array | cell array of character vectors

`Options` — Options for computing in parallel and setting random streams
structure

`mmdval` — Square MMD value
nonnegative scalar

`p` — p-value
scalar value in the range [0,1]

`h` — Hypothesis test result
`1` | `0`