resubPredict
Classify observations in multiclass error-correcting output codes (ECOC) model
Syntax
Description
label = resubPredict(Mdl)label) for the trained
multiclass error-correcting output codes (ECOC) model Mdl using the
predictor data stored in Mdl.X.
The software predicts the classification of an observation by assigning the observation to the class yielding the largest negated average binary loss (or, equivalently, the smallest average binary loss).
label = resubPredict(Mdl,Name,Value)
[
uses any of the input argument combinations in the previous syntaxes and additionally
returns the negated average binary loss per class
(label,NegLoss,PBScore]
= resubPredict(___)NegLoss) for observations, and the positive-class scores
(PBScore) for the observations classified by each binary
learner.
[
additionally returns posterior class probability estimates for observations
(label,NegLoss,PBScore,Posterior]
= resubPredict(___)Posterior).
To obtain posterior class probabilities, you must set
'FitPosterior',true when training the ECOC model using fitcecoc. Otherwise, resubPredict throws an error.
Examples
Load Fisher's iris data set. Specify the predictor data X, the response data Y, and the order of the classes in Y.
load fisheriris
X = meas;
Y = categorical(species);
classOrder = unique(Y);Train an ECOC model using SVM binary classifiers. Standardize the predictors using an SVM template, and specify the class order.
t = templateSVM('Standardize',true); Mdl = fitcecoc(X,Y,'Learners',t,'ClassNames',classOrder);
t is an SVM template object. During training, the software uses default values for empty properties in t. Mdl is a ClassificationECOC model.
Predict the labels of the training data. Print a random subset of true and predicted labels.
labels = resubPredict(Mdl); rng(1); % For reproducibility n = numel(Y); % Sample size idx = randsample(n,10); table(Y(idx),labels(idx),'VariableNames',{'TrueLabels','PredictedLabels'})
ans=10×2 table
TrueLabels PredictedLabels
__________ _______________
setosa setosa
versicolor versicolor
virginica virginica
setosa setosa
versicolor versicolor
setosa setosa
versicolor versicolor
versicolor versicolor
setosa setosa
setosa setosa
Mdl correctly labels the observations with indices idx.
Load Fisher's iris data set. Specify the predictor data X, the response data Y, and the order of the classes in Y.
load fisheriris X = meas; Y = categorical(species); classOrder = unique(Y); % Class order
Train an ECOC model using SVM binary classifiers. Standardize the predictors using an SVM template, and specify the class order.
t = templateSVM('Standardize',true); Mdl = fitcecoc(X,Y,'Learners',t,'ClassNames',classOrder);
t is an SVM template object. During training, the software uses default values for empty properties in t. Mdl is a ClassificationECOC model.
SVM scores are signed distances from the observation to the decision boundary. Therefore, the domain is . Create a custom binary loss function that does the following:
Map the coding design matrix (M) and positive-class classification scores (s) for each learner to the binary loss for each observation.
Use linear loss.
Aggregate the binary learner loss using the median.
You can create a separate function for the binary loss function, and then save it on the MATLAB® path. Or, you can specify an anonymous binary loss function. In this case, create a function handle (customBL) to an anonymous binary loss function.
customBL = @(M,s)median(1 - (M.*s),2,'omitnan')/2;Predict labels for the training data and estimate the median binary loss per class. Print the median negative binary losses per class for a random set of 10 observations.
[label,NegLoss] = resubPredict(Mdl,'BinaryLoss',customBL); rng(1); % For reproducibility n = numel(Y); % Sample size idx = randsample(n,10); classOrder
classOrder = 3×1 categorical
setosa
versicolor
virginica
table(Y(idx),label(idx),NegLoss(idx,:),'VariableNames',... {'TrueLabel','PredictedLabel','NegLoss'})
ans=10×3 table
TrueLabel PredictedLabel NegLoss
__________ ______________ _______________________________
setosa versicolor 0.12379 1.9569 -3.5807
versicolor versicolor -1.0172 0.62935 -1.1122
virginica virginica -1.9087 -0.21744 0.62617
setosa versicolor 0.4386 2.2441 -4.1827
versicolor versicolor -1.0735 0.39638 -0.82292
setosa versicolor 0.26672 2.2003 -3.967
versicolor versicolor -1.1237 0.69917 -1.0754
versicolor versicolor -1.2714 0.51834 -0.74695
setosa versicolor 0.35211 2.0677 -3.9198
setosa versicolor 0.23357 2.1885 -3.9221
The order of the columns corresponds to the elements of classOrder. The software predicts the label based on the maximum negated loss. The results indicate that the median of the linear losses might not perform as well as other losses.
Train an ECOC classifier using SVM binary learners. First predict the training-sample labels and class posterior probabilities. Then predict the maximum class posterior probability at each point in a grid. Visualize the results.
Load Fisher's iris data set. Specify the petal dimensions as the predictors and the species names as the response.
load fisheriris X = meas(:,3:4); Y = species; rng(1); % For reproducibility
Create an SVM template. Standardize the predictors, and specify the Gaussian kernel.
t = templateSVM('Standardize',true,'KernelFunction','gaussian');
t is an SVM template. Most of its properties are empty. When the software trains the ECOC classifier, it sets the applicable properties to their default values.
Train the ECOC classifier using the SVM template. Transform classification scores to class posterior probabilities (which are returned by predict or resubPredict) using the 'FitPosterior' name-value pair argument. Specify the class order using the 'ClassNames' name-value pair argument. Display diagnostic messages during training by using the 'Verbose' name-value pair argument.
Mdl = fitcecoc(X,Y,'Learners',t,'FitPosterior',true,... 'ClassNames',{'setosa','versicolor','virginica'},... 'Verbose',2);
Training binary learner 1 (SVM) out of 3 with 50 negative and 50 positive observations. Negative class indices: 2 Positive class indices: 1 Fitting posterior probabilities for learner 1 (SVM). Training binary learner 2 (SVM) out of 3 with 50 negative and 50 positive observations. Negative class indices: 3 Positive class indices: 1 Fitting posterior probabilities for learner 2 (SVM). Training binary learner 3 (SVM) out of 3 with 50 negative and 50 positive observations. Negative class indices: 3 Positive class indices: 2 Fitting posterior probabilities for learner 3 (SVM).
Mdl is a ClassificationECOC model. The same SVM template applies to each binary learner, but you can adjust options for each binary learner by passing in a cell vector of templates.
Predict the training-sample labels and class posterior probabilities. Display diagnostic messages during the computation of labels and class posterior probabilities by using the 'Verbose' name-value pair argument.
[label,~,~,Posterior] = resubPredict(Mdl,'Verbose',1);Predictions from all learners have been computed. Loss for all observations has been computed. Computing posterior probabilities...
Mdl.BinaryLoss
ans = 'quadratic'
The software assigns an observation to the class that yields the smallest average binary loss. Because all binary learners are computing posterior probabilities, the binary loss function is quadratic.
Display a random set of results.
idx = randsample(size(X,1),10,1); Mdl.ClassNames
ans = 3×1 cell
{'setosa' }
{'versicolor'}
{'virginica' }
table(Y(idx),label(idx),Posterior(idx,:),... 'VariableNames',{'TrueLabel','PredLabel','Posterior'})
ans=10×3 table
TrueLabel PredLabel Posterior
______________ ______________ ______________________________________
{'virginica' } {'virginica' } 0.0039322 0.003987 0.99208
{'virginica' } {'virginica' } 0.017067 0.018263 0.96467
{'virginica' } {'virginica' } 0.014948 0.015856 0.9692
{'versicolor'} {'versicolor'} 2.2197e-14 0.87318 0.12682
{'setosa' } {'setosa' } 0.999 0.00025092 0.00074638
{'versicolor'} {'virginica' } 2.2195e-14 0.05943 0.94057
{'versicolor'} {'versicolor'} 2.2194e-14 0.97001 0.029985
{'setosa' } {'setosa' } 0.999 0.00024991 0.0007474
{'versicolor'} {'versicolor'} 0.0085642 0.98259 0.0088487
{'setosa' } {'setosa' } 0.999 0.00025013 0.00074717
The columns of Posterior correspond to the class order of Mdl.ClassNames.
Define a grid of values in the observed predictor space. Predict the posterior probabilities for each instance in the grid.
xMax = max(X); xMin = min(X); x1Pts = linspace(xMin(1),xMax(1)); x2Pts = linspace(xMin(2),xMax(2)); [x1Grid,x2Grid] = meshgrid(x1Pts,x2Pts); [~,~,~,PosteriorRegion] = predict(Mdl,[x1Grid(:),x2Grid(:)]);
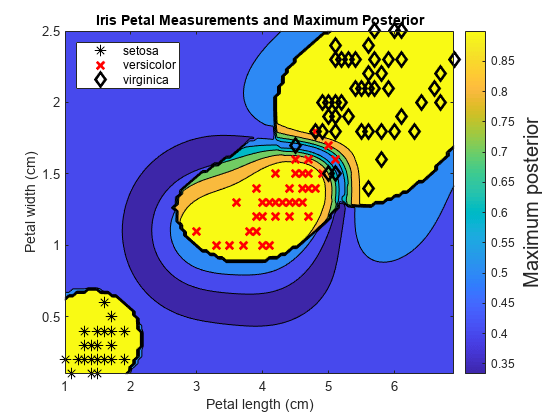
For each coordinate on the grid, plot the maximum class posterior probability among all classes.
contourf(x1Grid,x2Grid,... reshape(max(PosteriorRegion,[],2),size(x1Grid,1),size(x1Grid,2))); h = colorbar; h.YLabel.String = 'Maximum posterior'; h.YLabel.FontSize = 15; hold on gh = gscatter(X(:,1),X(:,2),Y,'krk','*xd',8); gh(2).LineWidth = 2; gh(3).LineWidth = 2; title('Iris Petal Measurements and Maximum Posterior') xlabel('Petal length (cm)') ylabel('Petal width (cm)') axis tight legend(gh,'Location','NorthWest') hold off
Train a multiclass ECOC model and estimate the posterior probabilities using parallel computing.
Load the arrhythmia data set. Examine the response data Y, and determine the number of classes.
load arrhythmia
Y = categorical(Y);
tabulate(Y) Value Count Percent
1 245 54.20%
2 44 9.73%
3 15 3.32%
4 15 3.32%
5 13 2.88%
6 25 5.53%
7 3 0.66%
8 2 0.44%
9 9 1.99%
10 50 11.06%
14 4 0.88%
15 5 1.11%
16 22 4.87%
K = numel(unique(Y));
Several classes are not represented in the data, and many other classes have low relative frequencies.
Specify an ensemble learning template that uses the GentleBoost method and 50 weak classification tree learners.
t = templateEnsemble('GentleBoost',50,'Tree');
t is a template object. Most of its properties are empty ([]). The software uses default values for all empty properties during training.
Because the response variable contains many classes, specify a sparse random coding design.
rng(1); % For reproducibility Coding = designecoc(K,'sparserandom');
Train an ECOC model using parallel computing. Specify to fit posterior probabilities.
pool = parpool; % Invokes workersStarting parallel pool (parpool) using the 'local' profile ... Connected to the parallel pool (number of workers: 6).
options = statset('UseParallel',true); Mdl = fitcecoc(X,Y,'Learner',t,'Options',options,'Coding',Coding,... 'FitPosterior',true);
Mdl is a ClassificationECOC model. You can access its properties using dot notation.
The pool invokes six workers, although the number of workers might vary among systems.
Estimate posterior probabilities, and display the posterior probability of being classified as not having arrhythmia (class 1) given a random subset of the training data.
[~,~,~,posterior] = resubPredict(Mdl); n = numel(Y); idx = randsample(n,10,1); table(idx,Y(idx),posterior(idx,1),... 'VariableNames',{'ObservationIndex','TrueLabel','PosteriorNoArrythmia'})
ans=10×3 table
ObservationIndex TrueLabel PosteriorNoArrythmia
________________ _________ ____________________
79 1 0.93436
248 1 0.95574
398 10 0.032378
207 1 0.97965
340 1 0.93656
206 1 0.97795
345 10 0.015642
296 2 0.13433
391 1 0.9648
406 1 0.94861
Input Arguments
Full, trained multiclass ECOC model, specified as a ClassificationECOC model trained with fitcecoc.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: resubPredict(Mdl,'BinaryLoss','linear','Decoding','lossbased')
specifies a linear binary learner loss function and a loss-based decoding scheme for
aggregating the binary losses.
Binary learner loss function, specified as a built-in loss function name or function handle.
This table describes the built-in functions, where yj is the class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss formula.
Value Description Score Domain g(yj,sj) "binodeviance"Binomial deviance (–∞,∞) log[1 + exp(–2yjsj)]/[2log(2)] "exponential"Exponential (–∞,∞) exp(–yjsj)/2 "hamming"Hamming [0,1] or (–∞,∞) [1 – sign(yjsj)]/2 "hinge"Hinge (–∞,∞) max(0,1 – yjsj)/2 "linear"Linear (–∞,∞) (1 – yjsj)/2 "logit"Logistic (–∞,∞) log[1 + exp(–yjsj)]/[2log(2)] "quadratic"Quadratic [0,1] [1 – yj(2sj – 1)]2/2 The software normalizes binary losses so that the loss is 0.5 when yj = 0. Also, the software calculates the mean binary loss for each class [1].
For a custom binary loss function, for example
customFunction, specify its function handleBinaryLoss=@customFunction.customFunctionhas this form:bLoss = customFunction(M,s)
Mis the K-by-B coding matrix stored inMdl.CodingMatrix.sis the 1-by-B row vector of classification scores.bLossis the classification loss. This scalar aggregates the binary losses for every learner in a particular class. For example, you can use the mean binary loss to aggregate the loss over the learners for each class.K is the number of classes.
B is the number of binary learners.
For an example of passing a custom binary loss function, see Predict Test-Sample Labels of ECOC Model Using Custom Binary Loss Function.
This table identifies the default BinaryLoss value, which depends on the
score ranges returned by the binary learners.
| Assumption | Default Value |
|---|---|
All binary learners are any of the following:
| "quadratic" |
| All binary learners are SVMs or linear or kernel classification models of SVM learners. | "hinge" |
All binary learners are ensembles trained by
AdaboostM1 or
GentleBoost. | "exponential" |
All binary learners are ensembles trained by
LogitBoost. | "binodeviance" |
You specify to predict class posterior probabilities by setting
FitPosterior=true in fitcecoc. | "quadratic" |
| Binary learners are heterogeneous and use different loss functions. | "hamming" |
To check the default value, use dot notation to display the BinaryLoss property of the trained model at the command line.
Example: BinaryLoss="binodeviance"
Data Types: char | string | function_handle
Decoding scheme that aggregates the binary losses, specified as
"lossweighted" or "lossbased". For more
information, see Binary Loss.
Example: Decoding="lossbased"
Data Types: char | string
Number of random initial values for fitting posterior probabilities by Kullback-Leibler
divergence minimization, specified as the comma-separated pair consisting of
'NumKLInitializations' and a nonnegative integer scalar.
If you do not request the fourth output argument (Posterior) and set
'PosteriorMethod','kl' (the default), then the software ignores
the value of NumKLInitializations.
For more details, see Posterior Estimation Using Kullback-Leibler Divergence.
Example: 'NumKLInitializations',5
Data Types: single | double
Estimation options, specified as a structure array as returned by statset.
To invoke parallel computing you need a Parallel Computing Toolbox™ license.
Example: Options=statset(UseParallel=true)
Data Types: struct
Posterior probability estimation method, specified as the comma-separated
pair consisting of 'PosteriorMethod' and 'kl' or 'qp'.
If
PosteriorMethodis'kl', then the software estimates multiclass posterior probabilities by minimizing the Kullback-Leibler divergence between the predicted and expected posterior probabilities returned by binary learners. For details, see Posterior Estimation Using Kullback-Leibler Divergence.If
PosteriorMethodis'qp', then the software estimates multiclass posterior probabilities by solving a least-squares problem using quadratic programming. You need an Optimization Toolbox™ license to use this option. For details, see Posterior Estimation Using Quadratic Programming.If you do not request the fourth output argument (
Posterior), then the software ignores the value ofPosteriorMethod.
Example: 'PosteriorMethod','qp'
Verbosity level, specified as 0 or 1.
Verbose controls the number of diagnostic messages that the
software displays in the Command Window.
If Verbose is 0, then the software does not display
diagnostic messages. Otherwise, the software displays diagnostic messages.
Example: Verbose=1
Data Types: single | double
Output Arguments
Predicted class labels, returned as a categorical or character array, logical or numeric vector, or cell array of character vectors.
label has the same data type as
Mdl.ClassNames and has the same number of rows as
Mdl.X.
The software predicts the classification of an observation by assigning the observation to the class yielding the largest negated average binary loss (or, equivalently, the smallest average binary loss).
Negated average binary losses, returned as a numeric matrix.
NegLoss is an n-by-K
matrix, where n is the number of observations
(size(Mdl.X,1)) and K is the number of unique
classes (size(Mdl.ClassNames,1)).
NegLoss(i,k) is the negated average binary loss for classifying observation
i into the kth class.
If
Decodingis'lossbased', thenNegLoss(i,k)is the negated sum of the binary losses divided by the total number of binary learners.If
Decodingis'lossweighted', thenNegLoss(i,k)is the negated sum of the binary losses divided by the number of binary learners for the kth class.
For more details, see Binary Loss.
Positive-class scores for each binary learner, returned as a numeric matrix.
PBScore is an n-by-B
matrix, where n is the number of observations
(size(Mdl.X,1)) and B is the number of binary
learners (size(Mdl.CodingMatrix,2)).
Posterior class probabilities, returned as a numeric matrix.
Posterior is an n-by-K
matrix, where n is the number of observations
(size(Mdl.X,1)) and K is the number of unique
classes (size(Mdl.ClassNames,1)).
To request Posterior, you must set
'FitPosterior',true when training the ECOC model using fitcecoc. Otherwise, the software throws an error.
More About
The binary loss is a function of the class and classification score that determines how well a binary learner classifies an observation into the class. The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation.
Assume the following:
mkj is element (k,j) of the coding design matrix M—that is, the code corresponding to class k of binary learner j. M is a K-by-B matrix, where K is the number of classes, and B is the number of binary learners.
sj is the score of binary learner j for an observation.
g is the binary loss function.
is the predicted class for the observation.
The software supports two decoding schemes:
Loss-based decoding [3] (
Decodingis"lossbased") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over all binary learners.Loss-weighted decoding [4] (
Decodingis"lossweighted") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over the binary learners for the corresponding class.The denominator corresponds to the number of binary learners for class k. [1] suggests that loss-weighted decoding improves classification accuracy by keeping loss values for all classes in the same dynamic range.
The predict, resubPredict, and
kfoldPredict functions return the negated value of the objective
function of argmin as the second output argument
(NegLoss) for each observation and class.
This table summarizes the supported binary loss functions, where yj is a class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss function.
| Value | Description | Score Domain | g(yj,sj) |
|---|---|---|---|
"binodeviance" | Binomial deviance | (–∞,∞) | log[1 + exp(–2yjsj)]/[2log(2)] |
"exponential" | Exponential | (–∞,∞) | exp(–yjsj)/2 |
"hamming" | Hamming | [0,1] or (–∞,∞) | [1 – sign(yjsj)]/2 |
"hinge" | Hinge | (–∞,∞) | max(0,1 – yjsj)/2 |
"linear" | Linear | (–∞,∞) | (1 – yjsj)/2 |
"logit" | Logistic | (–∞,∞) | log[1 + exp(–yjsj)]/[2log(2)] |
"quadratic" | Quadratic | [0,1] | [1 – yj(2sj – 1)]2/2 |
The software normalizes binary losses so that the loss is 0.5 when yj = 0, and aggregates using the average of the binary learners [1].
Do not confuse the binary loss with the overall classification loss (specified by the
LossFun name-value argument of the resubLoss and
resubPredict object functions), which measures how well an ECOC
classifier performs as a whole.
Algorithms
The software can estimate class posterior probabilities by minimizing the Kullback-Leibler divergence or by using quadratic programming. For the following descriptions of the posterior estimation algorithms, assume that:
mkj is the element (k,j) of the coding design matrix M.
I is the indicator function.
is the class posterior probability estimate for class k of an observation, k = 1,...,K.
rj is the positive-class posterior probability for binary learner j. That is, rj is the probability that binary learner j classifies an observation into the positive class, given the training data.
By default, the software minimizes the Kullback-Leibler divergence to estimate class posterior probabilities. The Kullback-Leibler divergence between the expected and observed positive-class posterior probabilities is
where is the weight for binary learner j.
Sj is the set of observation indices on which binary learner j is trained.
is the weight of observation i.
The software minimizes the divergence iteratively. The first step is to choose initial values for the class posterior probabilities.
If you do not specify
'NumKLIterations', then the software tries both sets of deterministic initial values described next, and selects the set that minimizes Δ.is the solution of the system
where M01 is M with all mkj = –1 replaced with 0, and r is a vector of positive-class posterior probabilities returned by the L binary learners [Dietterich et al.]. The software uses
lsqnonnegto solve the system.
If you specify
'NumKLIterations',c, wherecis a natural number, then the software does the following to choose the set , and selects the set that minimizes Δ.The software tries both sets of deterministic initial values as described previously.
The software randomly generates
cvectors of length K usingrand, and then normalizes each vector to sum to 1.
At iteration t, the software completes these steps:
Compute
Estimate the next class posterior probability using
Normalize so that they sum to 1.
Check for convergence.
For more details, see [Hastie et al.] and [Zadrozny].
Posterior probability estimation using quadratic programming requires an Optimization Toolbox license. To estimate posterior probabilities for an observation using this method, the software completes these steps:
Estimate the positive-class posterior probabilities, rj, for binary learners j = 1,...,L.
Using the relationship between rj and [Wu et al.], minimize
with respect to and the restrictions
The software performs minimization using
quadprog(Optimization Toolbox).
References
[1] Allwein, E., R. Schapire, and Y. Singer. “Reducing multiclass to binary: A unifying approach for margin classifiers.” Journal of Machine Learning Research. Vol. 1, 2000, pp. 113–141.
[2] Dietterich, T., and G. Bakiri. “Solving Multiclass Learning Problems Via Error-Correcting Output Codes.” Journal of Artificial Intelligence Research. Vol. 2, 1995, pp. 263–286.
[3] Escalera, S., O. Pujol, and P. Radeva. “Separability of ternary codes for sparse designs of error-correcting output codes.” Pattern Recog. Lett. Vol. 30, Issue 3, 2009, pp. 285–297.
[4] Escalera, S., O. Pujol, and P. Radeva. “On the decoding process in ternary error-correcting output codes.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 32, Issue 7, 2010, pp. 120–134.
[5] Hastie, T., and R. Tibshirani. “Classification by Pairwise Coupling.” Annals of Statistics. Vol. 26, Issue 2, 1998, pp. 451–471.
[6] Wu, T. F., C. J. Lin, and R. Weng. “Probability Estimates for Multi-Class Classification by Pairwise Coupling.” Journal of Machine Learning Research. Vol. 5, 2004, pp. 975–1005.
[7] Zadrozny, B. “Reducing Multiclass to Binary by Coupling Probability Estimates.” NIPS 2001: Proceedings of Advances in Neural Information Processing Systems 14, 2001, pp. 1041–1048.
Extended Capabilities
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2014b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)