copulaparam

Generate correlated random data from a beta distribution using a bivariate Gaussian copula with Kendall's tau rank correlation equal to -0.5.

Compute the linear correlation parameter from the rank correlation value.

rng default  % For reproducibility
tau = -0.5;
rho = copulaparam('Gaussian',tau)

rho = 
-0.7071

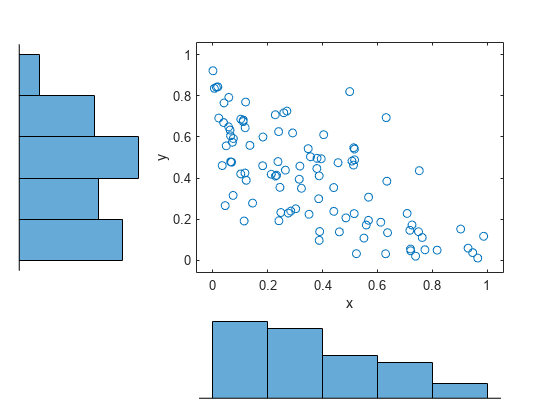
Use a Gaussian copula to generate a two-column matrix of dependent random values.

u = copularnd('gaussian',rho,100);

Each column contains 100 random values between 0 and 1, inclusive, sampled from a continuous uniform distribution.

Create a scatterhist plot to visualize the random numbers generated using the copula.

figure
scatterhist(u(:,1),u(:,2))

The histograms show that the data in each column of the copula has a marginal uniform distribution. The scatterplot shows that the data in the two columns is negatively correlated.

Use the inverse cdf function betainv to transform each column of the uniform marginal distributions into random numbers from a beta distribution. In the first column, the first shape parameter A is equal to 1, and a second shape parameter B is equal to 2. In the second column, the first shape parameter A is equal to 1.5, and a second shape parameter B is equal to 2.

b = [betainv(u(:,1),1,2), betainv(u(:,2),1.5,2)];

Create a scatterhist plot to visualize the correlated beta distribution data.

figure
scatterhist(b(:,1),b(:,2))

The histograms show the marginal beta distributions for each variable. The scatterplot shows the negative correlation.

Verify that the sample has a rank correlation approximately equal to the initial value for Kendall's tau.

tau_sample = corr(b,'type','kendall')

tau_sample = 2×2

    1.0000   -0.5135
   -0.5135    1.0000

The sample rank correlation of -0.5135 is approximately equal to the -0.5 initial value for tau.