曲线拟合和分布拟合

此示例说明如何执行曲线拟合和分布拟合，并讨论每种方法适用的情况。

在曲线拟合与分布拟合之间进行选择

曲线拟合和分布拟合是不同类型的数据分析。

当您要将某个响应变量建模为预测变量的函数时，请使用曲线拟合。
当您要为单一变量的概率分布建模时，请使用分布拟合。

曲线拟合

在以下试验数据中，预测变量为 time，即服用药物之后的时间。响应变量为 conc，即血液中的药物浓度。假设只有响应数据 conc 受试验误差的影响。

time = [ 0.1   0.1   0.3   0.3   1.3   1.7   2.1   2.6   3.9   3.9 ...
         5.1   5.6   6.2   6.4   7.7   8.1   8.2   8.9   9.0   9.5 ...
         9.6  10.2  10.3  10.8  11.2  11.2  11.2  11.7  12.1  12.3 ...
        12.3  13.1  13.2  13.4  13.7  14.0  14.3  15.4  16.1  16.1 ...
        16.4  16.4  16.7  16.7  17.5  17.6  18.1  18.5  19.3  19.7]';
conc = [0.01  0.08  0.13  0.16  0.55  0.90  1.11  1.62  1.79  1.59 ...
        1.83  1.68  2.09  2.17  2.66  2.08  2.26  1.65  1.70  2.39 ...
        2.08  2.02  1.65  1.96  1.91  1.30  1.62  1.57  1.32  1.56 ...
        1.36  1.05  1.29  1.32  1.20  1.10  0.88  0.63  0.69  0.69 ...
        0.49  0.53  0.42  0.48  0.41  0.27  0.36  0.33  0.17  0.20]';

假设您要将血液浓度建模为时间的函数。绘制 conc 对 time 的图。

plot(time,conc,'o');
xlabel('Time');
ylabel('Blood Concentration');

Figure contains an axes object. The axes object contains an object of type line.

假设 conc 作为 time 的函数，遵循双参数 Weibull 曲线。Weibull 曲线的形式和参数如下

$y = c (x / a)^{(b - 1)} e^{- (x / a)^{b}},$

其中， $a$ 是水平缩放， $b$ 是形状参数， $c$ 是垂直缩放。

使用非线性最小二乘来拟合 Weibull 模型。

modelFun =  @(p,x) p(3) .* (x./p(1)).^(p(2)-1) .* exp(-(x./p(1)).^p(2));
startingVals = [10 2 5];
nlModel = fitnlm(time,conc,modelFun,startingVals);

在数据上绘制 Weibull 曲线。

xgrid = linspace(0,20,100)';
line(xgrid,predict(nlModel,xgrid),'Color','r');

Figure contains an axes object. The axes object contains 2 objects of type line.

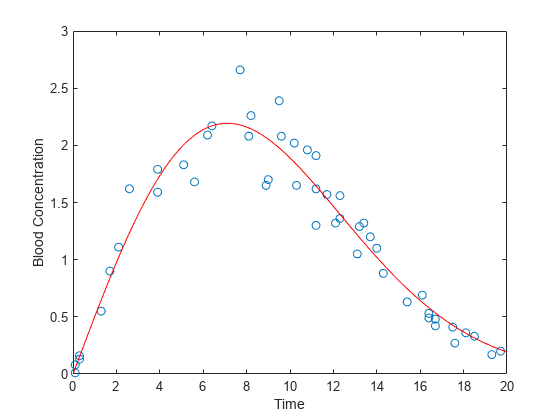
拟合的 Weibull 模型存在问题。fitnlm 假设试验误差为加性误差，并且来自具有常量方差的对称分布。但散点图显示，误差方差与曲线高度成正比。而且，加性对称误差意味着可能出现负的血液浓度测量值。

更加现实的假设是，乘性误差在对数尺度上对称。依据该假设，通过取两侧的对数，对数据进行 Weibull 曲线拟合。使用非线性最小二乘来拟合曲线：

$\log (y) = \log (c) + (b - 1) \log (x / a) - (x / a)^{b} .$

nlModel2 = fitnlm(time,log(conc),@(p,x) log(modelFun(p,x)),startingVals);

将新曲线添加到现有绘图。

line(xgrid,exp(predict(nlModel2,xgrid)),'Color',[0 .5 0],'LineStyle','--');
legend({'Raw Data','Additive Errors Model','Multiplicative Errors Model'});

Figure contains an axes object. The axes object contains 3 objects of type line. These objects represent Raw Data, Additive Errors Model, Multiplicative Errors Model.

模型对象 nlModel2 包含精度估计。最佳做法是检查模型的拟合优度。例如，在对数尺度上绘制残差图，以检验假设乘性误差具有常量方差是否正确。

在此示例中，使用乘性误差模型对模型预测的影响很小。有关模型类型影响较大的示例，请参阅 Pitfalls in Fitting Nonlinear Models by Transforming to Linearity。

曲线拟合函数

Statistics and Machine Learning Toolbox™ 包含以下用于拟合模型的函数：用于非线性最小二乘模型的 fitnlm、用于广义线性模型的 fitglm、用于高斯过程回归模型的 fitrgp 和用于支持向量机回归模型的 fitrsvm。
Curve Fitting Toolbox™ 提供了命令行和图形工具，可以简化曲线拟合中的任务。例如，该工具箱自动为各种模型选择起始系数值，并提供稳健和非参数拟合方法。
Optimization Toolbox™ 包含用于执行复杂类型的曲线拟合分析的函数，例如分析具有系数约束的模型。
MATLAB® 函数 polyfit 用于拟合多项式模型，而 MATLAB 函数 fminsearch 适用于其他种类的曲线拟合。

分布拟合

假设您要对电子元件使用寿命的分布进行建模。变量 life 用于测量 50 个完全相同的电子元件的失效时间。

life = [ 6.2 16.1 16.3 19.0 12.2  8.1  8.8  5.9  7.3  8.2 ...
        16.1 12.8  9.8 11.3  5.1 10.8  6.7  1.2  8.3  2.3 ...
         4.3  2.9 14.8  4.6  3.1 13.6 14.5  5.2  5.7  6.5 ...
         5.3  6.4  3.5 11.4  9.3 12.4 18.3 15.9  4.0 10.4 ...
         8.7  3.0 12.1  3.9  6.5  3.4  8.5  0.9  9.9  7.9]';

用直方图可视化数据。

binWidth = 2;
lastVal = ceil(max(life));
binEdges = 0:binWidth:lastVal+1;
h = histogram(life,binEdges);
xlabel('Time to Failure');
ylabel('Frequency');
ylim([0 10]);

Figure contains an axes object. The axes object contains an object of type histogram.

由于使用寿命数据通常遵循 Weibull 分布，因此可以使用前一个曲线拟合示例中的 Weibull 曲线来拟合直方图。要尝试此方法，请将直方图转换为一个 (x,y) 点集，其中 x 是 bin 中心，y 是 bin 高度，然后对这些点进行曲线拟合。

counts = histcounts(life,binEdges);
binCtrs = binEdges(1:end-1) + binWidth/2;
h.FaceColor = [.9 .9 .9];
hold on
plot(binCtrs,counts,'o');
hold off

Figure contains an axes object. The axes object contains 2 objects of type histogram, line.

但是，对直方图进行曲线拟合容易出现问题，通常不建议这样做。

该过程违背了最小二乘拟合的基本假设。bin 计数是非负值，这意味着测量误差不对称。而且，bin 计数在分布的尾部和中心具有不同的变异性。最后，bin 计数的总和是固定的，这意味着它们不是独立的测量值。
如果您对条形高度进行 Weibull 曲线拟合，则必须对曲线进行约束，因为直方图是经过缩放的经验概率密度函数 (pdf)。
对于连续数据，对直方图（而不是数据）进行曲线拟合会丢弃信息。
直方图的条形高度依赖于 bin 边界和 bin 宽度的选择。

对于许多参数化分布，最大似然是更好的参数估计方法，因为它能避免这些问题。Weibull pdf 与 Weibull 曲线具有几乎相同的形式：

$y = (b / a) (x / a)^{(b - 1)} e^{- (x / a)^{b}} .$

只不过 $b / a$ 取代了尺度参数 $c$ ，因为该函数的积分必须为 1。要使用最大似然对数据进行 Weibull 分布拟合，请使用 fitdist 并将 'Weibull' 指定为分布名称。与最小二乘不同，最大似然会找到与缩放后的直方图最匹配的 Weibull pdf，而无需最小化 pdf 与条形高度之差的平方和。

pd = fitdist(life,'Weibull');

绘制经过缩放的数据直方图，并叠加绘制拟合的 pdf。

h = histogram(life,binEdges,'Normalization','pdf','FaceColor',[.9 .9 .9]);
xlabel('Time to Failure');
ylabel('Probability Density');
ylim([0 0.1]);
xgrid = linspace(0,20,100)';
pdfEst = pdf(pd,xgrid);
line(xgrid,pdfEst)

Figure contains an axes object. The axes object contains 2 objects of type histogram, line.

最佳做法是检查模型的拟合优度。

尽管通常不建议对直方图进行曲线拟合，但在某些情况下这样做是合适的。有关示例，请参阅Fit Custom Distributions。

分布拟合函数

Statistics and Machine Learning Toolbox™ 包含用于对数据进行概率分布对象拟合的函数 fitdist。它还包括使用最大似然来拟合参数化分布的专用拟合函数（例如 wblfit）、用于拟合自定义分布（此时不使用专用拟合函数）的函数 mle，以及用于对数据进行非参数化分布模型拟合的函数 ksdensity。
Statistics and Machine Learning Toolbox 还提供了分布拟合器 App，它能简化分布拟合中的许多任务，例如生成可视化和诊断图。
利用 Optimization Toolbox™ 中的函数，您可以拟合复杂的分布，包括具有参数约束的分布。
MATLAB® 函数 fminsearch 提供最大似然分布拟合。

另请参阅