Main Content

fitcgam

Fit generalized additive model (GAM) for binary classification

Since R2021a

collapse all in page

Syntax

Mdl = fitcgam(Tbl,ResponseVarName)
Mdl = fitcgam(Tbl,formula)
Mdl = fitcgam(Tbl,Y)
Mdl = fitcgam(X,Y)
Mdl = fitcgam(___,Name,Value)
[Mdl,AggregateOptimizationResults] = fitcgam(___)

Description

Mdl = fitcgam(Tbl,ResponseVarName) returns a generalized additive model Mdl trained using the sample data contained in the table Tbl. The input argument ResponseVarName is the name of the variable in Tbl that contains the class labels for binary classification.

example

Mdl = fitcgam(Tbl,formula) uses the model specification argument formula to specify the class labels and predictor variables in Tbl. You can specify a subset of predictor variables and interaction terms for predictor variables by using formula.

example

Mdl = fitcgam(Tbl,Y) uses the predictor variables in the table Tbl and the class labels in the vector Y.

Mdl = fitcgam(X,Y) uses the predictors in the matrix X and the class labels in the vector Y.

example

Mdl = fitcgam(___,Name,Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in the previous syntaxes. For example, 'Interactions',5 specifies to include five interaction terms in the model. You can also specify a list of interaction terms using the Interactions name-value argument.

example

[Mdl,AggregateOptimizationResults] = fitcgam(___) also returns AggregateOptimizationResults, which contains hyperparameter optimization results when you specify the OptimizeHyperparameters and HyperparameterOptimizationOptions name-value arguments. You must also specify the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions. You can use this syntax to optimize on compact model size instead of cross-validation loss, and to perform a set of multiple optimization problems that have the same options but different constraint bounds.

Examples

collapse all

Open Live Script

Train a univariate generalized additive model, which contains linear terms for predictors. Then, interpret the prediction for a specified data instance by using the plotLocalEffects function.

Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').

load ionosphere

Train a univariate GAM that identifies whether the radar return is bad ('b') or good ('g'). 

Mdl = fitcgam(X,Y)
Mdl = 
  ClassificationGAM
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: {'b'  'g'}
           ScoreTransform: 'logit'
                Intercept: 2.2715
          NumObservations: 351

Mdl is a ClassificationGAM model object. The model display shows a partial list of the model properties. To view the full list of properties, double-click the variable name Mdl in the Workspace. The Variables editor opens for Mdl. Alternatively, you can display the properties in the Command Window by using dot notation. For example, display the class order of Mdl.

classOrder = Mdl.ClassNames
classOrder = 2x1 cell
    {'b'}
    {'g'}

Classify the first observation of the training data, and plot the local effects of the terms in Mdl on the prediction.

label = predict(Mdl,X(1,:))
label = 1x1 cell array
    {'g'}


plotLocalEffects(Mdl,X(1,:))

Figure contains an axes object. The axes object with title Local Effects Plot, xlabel Local Effect, ylabel Term contains an object of type bar.

The predict function classifies the first observation X(1,:) as 'g'. The plotLocalEffects function creates a horizontal bar graph that shows the local effects of the 10 most important terms on the prediction. Each local effect value shows the contribution of each term to the classification score for 'g', which is the logit of the posterior probability that the classification is 'g' for the observation.

Open Live Script

Train a generalized additive model that contains linear and interaction terms for predictors in three different ways:

  • Specify the interaction terms using the formula input argument.

  • Specify the 'Interactions' name-value argument.

  • Build a model with linear terms first and add interaction terms to the model by using the addInteractions function.

Load Fisher's iris data set. Create a table that contains observations for versicolor and virginica.

load fisheriris
inds = strcmp(species,'versicolor') | strcmp(species,'virginica');
tbl = array2table(meas(inds,:),'VariableNames',["x1","x2","x3","x4"]);
tbl.Y = species(inds,:);

Specify formula

Train a GAM that contains the four linear terms (x1, x2, x3, and x4) and two interaction terms (x1*x2 and x2*x3). Specify the terms using a formula in the form 'Y ~ terms'.

Mdl1 = fitcgam(tbl,'Y ~ x1 + x2 + x3 + x4 + x1:x2 + x2:x3');

The function adds interaction terms to the model in the order of importance. You can use the Interactions property to check the interaction terms in the model and the order in which fitcgam adds them to the model. Display the Interactions property.

Mdl1.Interactions
ans = 2×2

     2     3
     1     2

Each row of Interactions represents one interaction term and contains the column indexes of the predictor variables for the interaction term.

Specify 'Interactions'

Pass the training data (tbl) and the name of the response variable in tbl to fitcgam, so that the function includes the linear terms for all the other variables as predictors. Specify the 'Interactions' name-value argument using a logical matrix to include the two interaction terms, x1*x2 and x2*x3. 

Mdl2 = fitcgam(tbl,'Y','Interactions',logical([1 1 0 0; 0 1 1 0]));
Mdl2.Interactions
ans = 2×2

     2     3
     1     2

You can also specify 'Interactions' as the number of interaction terms or as 'all' to include all available interaction terms. Among the specified interaction terms, fitcgam identifies those whose p-values are not greater than the 'MaxPValue' value and adds them to the model. The default 'MaxPValue' is 1 so that the function adds all specified interaction terms to the model.

Specify 'Interactions','all' and set the 'MaxPValue' name-value argument to 0.01.

Mdl3 = fitcgam(tbl,'Y','Interactions','all','MaxPValue',0.01);
Mdl3.Interactions
ans = 5×2

     3     4
     2     4
     1     4
     2     3
     1     3

Mdl3 includes five of the six available pairs of interaction terms.

Use addInteractions Function

Train a univariate GAM that contains linear terms for predictors, and then add interaction terms to the trained model by using the addInteractions function. Specify the second input argument of addInteractions in the same way you specify the 'Interactions' name-value argument of fitcgam. You can specify the list of interaction terms using a logical matrix, the number of interaction terms, or 'all'.

Specify the number of interaction terms as 5 to add the five most important interaction terms to the trained model.

Mdl4 = fitcgam(tbl,'Y');
UpdatedMdl4 = addInteractions(Mdl4,5);
UpdatedMdl4.Interactions
ans = 5×2

     3     4
     2     4
     1     4
     2     3
     1     3

Mdl4 is a univariate GAM, and UpdatedMdl4 is an updated GAM that contains all the terms in Mdl4 and five additional interaction terms.

Open Live Script

Train a cross-validated GAM with 10 folds, which is the default cross-validation option, by using fitcgam. Then, use kfoldPredict to predict class labels for validation-fold observations using a model trained on training-fold observations.

Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').

load ionosphere

Create a cross-validated GAM by using the default cross-validation option. Specify the 'CrossVal' name-value argument as 'on'. 

rng('default') % For reproducibility
CVMdl = fitcgam(X,Y,'CrossVal','on')
CVMdl = 
  ClassificationPartitionedGAM
    CrossValidatedModel: 'GAM'
         PredictorNames: {'x1'  'x2'  'x3'  'x4'  'x5'  'x6'  'x7'  'x8'  'x9'  'x10'  'x11'  'x12'  'x13'  'x14'  'x15'  'x16'  'x17'  'x18'  'x19'  'x20'  'x21'  'x22'  'x23'  'x24'  'x25'  'x26'  'x27'  'x28'  'x29'  'x30'  'x31'  'x32'  'x33'  'x34'}
           ResponseName: 'Y'
        NumObservations: 351
                  KFold: 10
              Partition: [1x1 cvpartition]
      NumTrainedPerFold: [1x1 struct]
             ClassNames: {'b'  'g'}
         ScoreTransform: 'logit'

The fitcgam function creates a ClassificationPartitionedGAM model object CVMdl with 10 folds. During cross-validation, the software completes these steps:

  1. Randomly partition the data into 10 sets.

  2. For each set, reserve the set as validation data, and train the model using the other 9 sets.

  3. Store the 10 compact, trained models in a 10-by-1 cell vector in the Trained property of the cross-validated model object ClassificationPartitionedGAM.

You can override the default cross-validation setting by using the 'CVPartition', 'Holdout', 'KFold', or 'Leaveout' name-value argument.

Classify the observations in X by using kfoldPredict. The function predicts class labels for every observation using the model trained without that observation.

label = kfoldPredict(CVMdl);

Create a confusion matrix to compare the true classes of the observations to their predicted labels.

C = confusionchart(Y,label);

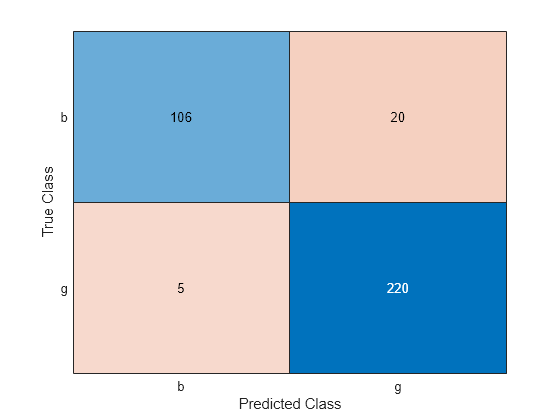
Figure contains an object of type ConfusionMatrixChart.

Compute the classification error.

L = kfoldLoss(CVMdl)
L = 
0.0712

The average misclassification rate over 10 folds is about 7%.

Open Live Script

Optimize the hyperparameters of a GAM with respect to cross-validation loss by using the OptimizeHyperparameters name-value argument.

Load the 1994 census data stored in census1994.mat. The data set consists of demographic data from the US Census Bureau to predict whether an individual makes over $50,000 per year. The classification task is to fit a model that predicts the salary category of people given their age, working class, education level, marital status, race, and so on.

load census1994

census1994 contains the training data set adultdata and the test data set adulttest. To reduce the running time for this example, subsample 500 training observations and 500 test observations by using the datasample function. 

rng('default')
NumSamples = 5e2;
adultdata = datasample(adultdata,NumSamples,'Replace',false);
adulttest = datasample(adulttest,NumSamples,'Replace',false);

Train a GAM classifier by passing the training data adultdata to the fitcgam function, and include the OptimizeHyperparameters argument. Specify OptimizeHyperparameters as 'auto' so that fitcgam finds optimal values of InitialLearnRateForPredictors, NumTreesPerPredictor, Interactions, InitialLearnRateForInteractions, and NumTreesPerInteraction. For reproducibility, choose the 'expected-improvement-plus' acquisition function. The default acquisition function depends on run time and, therefore, can give varying results.

Mdl = fitcgam(adultdata,'salary','OptimizeHyperparameters','auto', ...
    'HyperparameterOptimizationOptions', ...
    struct('AcquisitionFunctionName','expected-improvement-plus'))
|==========================================================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | InitialLearnRate-| NumTreesPerP-| Interactions | InitialLearnRate-| NumTreesPerI-|
|      | result |             | runtime     | (observed)  | (estim.)    | ForPredictors    | redictor     |              | ForInteractions  | nteraction   |
|==========================================================================================================================================================|
|    1 | Best   |       0.148 |      11.721 |       0.148 |       0.148 |         0.001555 |          356 |            5 |         0.068117 |           16 |
|    2 | Accept |       0.182 |     0.88258 |       0.148 |     0.14977 |          0.94993 |           25 |            0 |                - |            - |
|    3 | Accept |       0.174 |      0.5938 |       0.148 |       0.148 |         0.016784 |           11 |            3 |          0.12025 |           12 |
|    4 | Accept |       0.176 |      10.466 |       0.148 |       0.148 |          0.14207 |          179 |           71 |        0.0020629 |           22 |
|    5 | Accept |       0.176 |      9.6859 |       0.148 |      0.1502 |        0.0010025 |          104 |           12 |        0.0052651 |          178 |
|    6 | Accept |       0.152 |       9.212 |       0.148 |     0.15035 |        0.0017566 |          323 |            4 |         0.079281 |           16 |
|    7 | Accept |       0.166 |      16.319 |       0.148 |     0.14801 |        0.0011656 |          497 |           10 |          0.17479 |           92 |
|    8 | Accept |       0.172 |       10.99 |       0.148 |     0.14914 |        0.0014435 |          397 |            0 |                - |            - |
|    9 | Accept |        0.16 |        11.9 |       0.148 |     0.14801 |        0.0016398 |          432 |            2 |         0.045129 |           11 |
|   10 | Accept |       0.172 |       4.414 |       0.148 |     0.14855 |        0.0013589 |          146 |            9 |         0.065204 |           12 |
|   11 | Accept |       0.156 |      10.724 |       0.148 |     0.14911 |         0.002082 |          368 |            7 |        0.0011513 |           12 |
|   12 | Accept |       0.178 |      11.031 |       0.148 |     0.14801 |          0.13309 |          360 |            6 |          0.67104 |           13 |
|   13 | Accept |       0.154 |      11.475 |       0.148 |     0.15192 |        0.0014287 |          380 |            5 |         0.027919 |           18 |
|   14 | Accept |       0.164 |      10.497 |       0.148 |     0.15151 |        0.0015368 |          318 |            5 |         0.022401 |           93 |
|   15 | Best   |       0.144 |      9.6966 |       0.144 |     0.14515 |        0.0020403 |          331 |            8 |          0.12167 |           11 |
|   16 | Accept |       0.168 |      9.6039 |       0.144 |     0.14401 |        0.0016201 |          329 |           10 |          0.74319 |           12 |
|   17 | Accept |        0.16 |      9.0822 |       0.144 |      0.1526 |         0.002317 |          313 |            9 |         0.093554 |           18 |
|   18 | Accept |       0.158 |      9.8266 |       0.144 |     0.15425 |        0.0016865 |          331 |            5 |         0.023535 |           11 |
|   19 | Accept |       0.146 |      11.464 |       0.144 |     0.15096 |        0.0019238 |          386 |            6 |         0.043578 |           14 |
|   20 | Accept |       0.156 |      11.165 |       0.144 |     0.15234 |        0.0023502 |          385 |            6 |         0.063029 |           11 |
|==========================================================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | InitialLearnRate-| NumTreesPerP-| Interactions | InitialLearnRate-| NumTreesPerI-|
|      | result |             | runtime     | (observed)  | (estim.)    | ForPredictors    | redictor     |              | ForInteractions  | nteraction   |
|==========================================================================================================================================================|
|   21 | Accept |       0.146 |      11.203 |       0.144 |     0.15105 |        0.0023381 |          383 |            6 |         0.042149 |           21 |
|   22 | Best   |       0.142 |      11.922 |       0.142 |     0.14959 |        0.0024173 |          400 |            7 |         0.022884 |           18 |
|   23 | Accept |       0.152 |      13.325 |       0.142 |     0.14972 |        0.0017718 |          443 |            8 |         0.022974 |           18 |
|   24 | Best   |        0.14 |      12.785 |        0.14 |     0.14681 |        0.0032302 |          417 |            7 |          0.01295 |           23 |
|   25 | Accept |       0.148 |      11.121 |        0.14 |     0.14672 |        0.0043102 |          371 |            6 |         0.016624 |           27 |
|   26 | Accept |        0.14 |      11.871 |        0.14 |     0.14433 |        0.0029528 |          410 |            6 |         0.011766 |           25 |
|   27 | Accept |        0.15 |      13.058 |        0.14 |     0.14441 |        0.0038288 |          455 |            6 |         0.038686 |           14 |
|   28 | Accept |       0.144 |      13.992 |        0.14 |     0.14374 |        0.0030969 |          471 |            7 |        0.0093565 |           39 |
|   29 | Accept |       0.144 |      14.149 |        0.14 |     0.14331 |        0.0033063 |          487 |            5 |        0.0033831 |           26 |
|   30 | Best   |       0.138 |      12.442 |       0.138 |     0.14213 |        0.0031221 |          420 |            5 |        0.0035267 |           26 |


__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 326.2596 seconds
Total objective function evaluation time: 316.6185

Best observed feasible point:
    InitialLearnRateForPredictors    NumTreesPerPredictor    Interactions    InitialLearnRateForInteractions    NumTreesPerInteraction
    _____________________________    ____________________    ____________    _______________________________    ______________________

              0.0031221                      420                  5                     0.0035267                         26          

Observed objective function value = 0.138
Estimated objective function value = 0.14267
Function evaluation time = 12.4417

Best estimated feasible point (according to models):
    InitialLearnRateForPredictors    NumTreesPerPredictor    Interactions    InitialLearnRateForInteractions    NumTreesPerInteraction
    _____________________________    ____________________    ____________    _______________________________    ______________________

              0.0029528                      410                  6                     0.011766                          25          

Estimated objective function value = 0.14213
Estimated function evaluation time = 12.2594

Mdl = 
  ClassificationGAM
                       PredictorNames: {'age'  'workClass'  'fnlwgt'  'education'  'education_num'  'marital_status'  'occupation'  'relationship'  'race'  'sex'  'capital_gain'  'capital_loss'  'hours_per_week'  'native_country'}
                         ResponseName: 'salary'
                CategoricalPredictors: [2 4 6 7 8 9 10 14]
                           ClassNames: [<=50K    >50K]
                       ScoreTransform: 'logit'
                            Intercept: -1.3924
                         Interactions: [6×2 double]
                      NumObservations: 500
    HyperparameterOptimizationResults: [1×1 BayesianOptimization]


  Properties, Methods

fitcgam returns a ClassificationGAM model object that uses the best estimated feasible point. The best estimated feasible point is the set of hyperparameters that minimizes the upper confidence bound of the cross-validation loss based on the underlying Gaussian process model of the Bayesian optimization process.

The Bayesian optimization process internally maintains a Gaussian process model of the objective function. The objective function is the cross-validated misclassification rate for classification. For each iteration, the optimization process updates the Gaussian process model and uses the model to find a new set of hyperparameters. Each line of the iterative display shows the new set of hyperparameters and these column values:

  • Objective — Objective function value computed at the new set of hyperparameters.

  • Objective runtime — Objective function evaluation time.

  • Eval result — Result report, specified as Accept, Best, or Error. Accept indicates that the objective function returns a finite value, and Error indicates that the objective function returns a value that is not a finite real scalar. Best indicates that the objective function returns a finite value that is lower than previously computed objective function values.

  • BestSoFar(observed) — The minimum objective function value computed so far. This value is either the objective function value of the current iteration (if the Eval result value for the current iteration is Best) or the value of the previous Best iteration.

  • BestSoFar(estim.) — At each iteration, the software estimates the upper confidence bounds of the objective function values, using the updated Gaussian process model, at all the sets of hyperparameters tried so far. Then the software chooses the point with the minimum upper confidence bound. The BestSoFar(estim.) value is the objective function value returned by the predictObjective function at the minimum point.

The plot below the iterative display shows the BestSoFar(observed) and BestSoFar(estim.) values in blue and green, respectively.

The returned object Mdl uses the best estimated feasible point, that is, the set of hyperparameters that produces the BestSoFar(estim.) value in the final iteration based on the final Gaussian process model.

Obtain the best estimated feasible point from Mdl in the HyperparameterOptimizationResults property.

Mdl.HyperparameterOptimizationResults.XAtMinEstimatedObjective
ans=1×5 table
    InitialLearnRateForPredictors    NumTreesPerPredictor    Interactions    InitialLearnRateForInteractions    NumTreesPerInteraction
    _____________________________    ____________________    ____________    _______________________________    ______________________

              0.0029528                      410                  6                     0.011766                          25

Alternatively, you can use the bestPoint function. By default, the bestPoint function uses the 'min-visited-upper-confidence-interval' criterion.

[x,CriterionValue,iteration] = bestPoint(Mdl.HyperparameterOptimizationResults)
x=1×5 table
    InitialLearnRateForPredictors    NumTreesPerPredictor    Interactions    InitialLearnRateForInteractions    NumTreesPerInteraction
    _____________________________    ____________________    ____________    _______________________________    ______________________

              0.0029528                      410                  6                     0.011766                          25          


CriterionValue = 0.1464

iteration = 26

The 'min-visited-upper-confidence-interval' criterion chooses the hyperparameters obtained from the 26th iteration as the best point. CriterionValue is the upper bound of the cross-validated loss computed by the final Gaussian process model.

You can also extract the best observed feasible point (that is, the last Best point in the iterative display) from the HyperparameterOptimizationResults property or by specifying Criterion as 'min-observed'.

Mdl.HyperparameterOptimizationResults.XAtMinObjective
ans=1×5 table
    InitialLearnRateForPredictors    NumTreesPerPredictor    Interactions    InitialLearnRateForInteractions    NumTreesPerInteraction
    _____________________________    ____________________    ____________    _______________________________    ______________________

              0.0031221                      420                  5                     0.0035267                         26          


[x_observed,CriterionValue_observed,iteration_observed] = bestPoint(Mdl.HyperparameterOptimizationResults,'Criterion','min-observed')
x_observed=1×5 table
    InitialLearnRateForPredictors    NumTreesPerPredictor    Interactions    InitialLearnRateForInteractions    NumTreesPerInteraction
    _____________________________    ____________________    ____________    _______________________________    ______________________

              0.0031221                      420                  5                     0.0035267                         26          


CriterionValue_observed = 0.1380

iteration_observed = 30

The 'min-observed' criterion chooses the hyperparameters obtained from the 30th iteration as the best point. CriterionValue_observed is the actual cross-validated loss computed using the selected hyperparameters. For more information, see the Criterion name-value argument of bestPoint.

Evaluate the performance of the classifier on the test set by computing the test set classification error. 

L = loss(Mdl,adulttest,'salary')
L = 0.1564
Open Live Script

Optimize the parameters of a GAM with respect to cross-validation by using the bayesopt function.

Alternatively, you can find optimal values of fitcgam name-value arguments by using the OptimizeHyperparameters name-value argument. For an example, see Optimize GAM Using OptimizeHyperparameters.

Load the 1994 census data stored in census1994.mat. The data set consists of demographic data from the US Census Bureau to predict whether an individual makes over $50,000 per year. The classification task is to fit a model that predicts the salary category of people given their age, working class, education level, marital status, race, and so on.

load census1994

census1994 contains the training data set adultdata and the test data set adulttest. To reduce the running time for this example, subsample 500 training observations from adultdata by using the datasample function. 

rng('default')
NumSamples = 5e2;
adultdata = datasample(adultdata,NumSamples,'Replace',false);

Set up a partition for cross-validation. This step fixes the cross-validation sets that the optimization uses at each step.

c = cvpartition(adultdata.salary,'KFold',5);

Prepare optimizableVariable objects for the name-value arguments that you want to optimize using Bayesian optimization. This example finds optimal values for the MaxNumSplitsPerPredictor and NumTreesPerPredictor arguments of fitcgam.

maxNumSplits = optimizableVariable('maxNumSplits',[1,10],'Type','integer');
numTrees = optimizableVariable('numTrees',[1,500],'Type','integer');

Create an objective function that takes an input z = [maxNumSplits,numTrees] and returns the cross-validated loss value of z.

minfun = @(z)kfoldLoss(fitcgam(adultdata,'salary','CVPartition',c, ...
    'MaxNumSplitsPerPredictor',z.maxNumSplits, ...
    'NumTreesPerPredictor',z.numTrees));

If you specify a cross-validation option, then the fitcgam function returns a cross-validated model object ClassificationPartitionedGAM. The kfoldLoss function returns the classification loss obtained by the cross-validated model. Therefore, the function handle minfun computes the cross-validation loss at the parameters in z.

Search for the best parameters [maxNumSplits,numTrees] using bayesopt. For reproducibility, choose the 'expected-improvement-plus' acquisition function. The default acquisition function depends on run time and, therefore, can give varying results. 

results = bayesopt(minfun,[maxNumSplits,numTrees],'Verbose',0, ...
    'IsObjectiveDeterministic',true, ...
    'AcquisitionFunctionName','expected-improvement-plus');

Obtain the best point from results.

zbest = bestPoint(results)
zbest=1×2 table
    maxNumSplits    numTrees
    ____________    ________

         1             5

Train an optimized GAM using the zbest values.

Mdl = fitcgam(adultdata,'salary', ...
    'MaxNumSplitsPerPredictor',zbest.maxNumSplits, ...
    'NumTreesPerPredictor',zbest.numTrees);

Input Arguments

collapse all

Sample data used to train the model, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one predictor variable. Multicolumn variables and cell arrays other than cell arrays of character vectors are not allowed.

Optionally, Tbl can contain a column for the response variable and a column for the observation weights.

  • The response variable must be a categorical, character, or string array, a logical or numeric vector, or a cell array of character vectors.

    • fitcgam supports only binary classification. Either the response variable must contain exactly two distinct classes, or you must specify two classes for training by using the ClassNames name-value argument.

    • A good practice is to specify the order of the classes in the response variable by using the ClassNames name-value argument.

  • The column for the weights must be a numeric vector.

  • You must specify the response variable in Tbl by using ResponseVarName or formula and specify the observation weights in Tbl by using Weights.

    • Specify the response variable by using ResponseVarName — fitcgam uses the remaining variables as predictors. To use a subset of the remaining variables in Tbl as predictors, specify predictor variables by using PredictorNames.

    • Define a model specification by using formula — fitcgam uses a subset of the variables in Tbl as predictor variables and the response variable, as specified in formula.

If Tbl does not contain the response variable, then specify a response variable by using Y. The length of the response variable Y and the number of rows in Tbl must be equal. To use a subset of the variables in Tbl as predictors, specify predictor variables by using PredictorNames.

fitcgam considers NaN, '' (empty character vector), "" (empty string), <missing>, and <undefined> values in Tbl to be missing values.

  • fitcgam does not use observations with all missing values in the fit.

  • fitcgam does not use observations with missing response values in the fit.

  • fitcgam uses observations with some missing values for predictors to find splits on variables for which these observations have valid values.

Data Types: table

Response variable name, specified as a character vector or string scalar containing the name of the response variable in Tbl. For example, if the response variable Y is stored in Tbl.Y, then specify it as 'Y'.

Data Types: char | string

Model specification, specified as a character vector or string scalar in the form 'Y ~ terms'. The formula argument specifies a response variable and linear and interaction terms for predictor variables. Use formula to specify a subset of variables in Tbl as predictors for training the model. If you specify a formula, then the software does not use any variables in Tbl that do not appear in formula.

For example, specify 'Y~x1+x2+x3+x1:x2'. In this form, Y represents the response variable, and x1, x2, and x3 represent the linear terms for the predictor variables. x1:x2 represents the interaction term for x1 and x2.

The variable names in the formula must be both variable names in Tbl (Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by using the isvarname function. If the variable names are not valid, then you can convert them by using the matlab.lang.makeValidName function.

Alternatively, you can specify a response variable and linear terms for predictors using formula, and specify interaction terms for predictors using 'Interactions'.

fitcgam builds a set of interaction trees using only the terms whose p-values are not greater than the 'MaxPValue' value.

Example: 'Y~x1+x2+x3+x1:x2'

Data Types: char | string

Class labels, specified as a categorical, character, or string array, a logical or numeric vector, or a cell array of character vectors.

  • fitcgam supports only binary classification. Either Y must contain exactly two distinct classes, or you must specify two classes for training by using the ClassNames name-value argument.

  • The length of Y must be equal to the number of observations in X or Tbl.

  • If Y is a character array, then each label must correspond to one row of the array.

  • A good practice is to specify the class order using the ClassNames name-value pair argument.

  • fitcgam considers NaN, '' (empty character vector), "" (empty string), <missing>, and <undefined> values in Y to be missing values. fitcgam does not use observations with missing response values in the fit.

Data Types: single | double | categorical | logical | char | string | cell

Predictor data, specified as a numeric matrix. Each row of X corresponds to one observation, and each column corresponds to one predictor variable.

fitcgam considers NaN values in X as missing values. The function does not use observations with all missing values in the fit. fitcgam uses observations with some missing values for X to find splits on variables for which these observations have valid values.

Data Types: single | double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Interactions','all','MaxPValue',0.05 specifies to include all available interaction terms whose p-values are not greater than 0.05.

GAM Options

collapse all

Initial learning rate of gradient boosting for interaction terms, specified as a numeric scalar in the interval (0,1].

For each boosting iteration for interaction trees, fitcgam starts fitting with the initial learning rate. The function halves the learning rate until it finds a rate that improves the model fit.

Training a model using a small learning rate requires more learning iterations, but often achieves better accuracy.

For more details about gradient boosting, see Gradient Boosting Algorithm.

Example: 'InitialLearnRateForInteractions',0.1

Data Types: single | double

Initial learning rate of gradient boosting for linear terms, specified as a numeric scalar in the interval (0,1].

For each boosting iteration for predictor trees, fitcgam starts fitting with the initial learning rate. The function halves the learning rate until it finds a rate that improves the model fit.

Training a model using a small learning rate requires more learning iterations, but often achieves better accuracy.

For more details about gradient boosting, see Gradient Boosting Algorithm.

Example: 'InitialLearnRateForPredictors',0.1

Data Types: single | double

Number or list of interaction terms to include in the candidate set S, specified as a nonnegative integer scalar, a logical matrix, or 'all'.

  • Number of interaction terms, specified as a nonnegative integer — S includes the specified number of important interaction terms, selected based on the p-values of the terms.

  • List of interaction terms, specified as a logical matrix — S includes the terms specified by a t-by-p logical matrix, where t is the number of interaction terms, and p is the number of predictors used to train the model. For example, logical([1 1 0; 0 1 1]) represents two pairs of interaction terms: a pair of the first and second predictors, and a pair of the second and third predictors.

    If fitcgam uses a subset of input variables as predictors, then the function indexes the predictors using only the subset. That is, the column indexes of the logical matrix do not count the response and observation weight variables. The indexes also do not count any variables not used by the function.

  • 'all' — S includes all possible pairs of interaction terms, which is p*(p – 1)/2 number of terms in total.

Among the interaction terms in S, the fitcgam function identifies those whose p-values are not greater than the 'MaxPValue' value and uses them to build a set of interaction trees. Use the default value ('MaxPValue',1) to build interaction trees using all terms in S.

Example: 'Interactions','all'

Data Types: single | double | logical | char | string

Maximum number of decision splits (or branch nodes) for each interaction tree (boosted tree for an interaction term), specified as a positive integer scalar.

Example: 'MaxNumSplitsPerInteraction',5

Data Types: single | double

Maximum number of decision splits (or branch nodes) for each predictor tree (boosted tree for a linear term), specified as a positive integer scalar. By default, fitcgam uses a tree stump for a predictor tree.

Example: 'MaxNumSplitsPerPredictor',5

Data Types: single | double

Maximum p-value for detecting interaction terms, specified as a numeric scalar in the interval [0,1].

fitcgam first finds the candidate set S of interaction terms from formula or 'Interactions'. Then the function identifies the interaction terms whose p-values are not greater than the 'MaxPValue' value and uses them to build a set of interaction trees.

The default value ('MaxPValue',1) builds interaction trees for all interaction terms in the candidate set S.

For more details about detecting interaction terms, see Interaction Term Detection.

Example: 'MaxPValue',0.05

Data Types: single | double

Number of bins for numeric predictors, specified as a positive integer scalar or [] (empty).

  • If you specify the 'NumBins' value as a positive integer scalar (numBins), then fitcgam bins every numeric predictor into at most numBins equiprobable bins, and then grows trees on the bin indices instead of the original data.

    • The number of bins can be less than numBins if a predictor has fewer than numBins unique values.

    • fitcgam does not bin categorical predictors.

  • If the 'NumBins' value is empty ([]), then fitcgam does not bin any predictors.

When you use a large training data set, this binning option speeds up training but might cause a decrease in accuracy. You can first use the default value of 'NumBins', and then change the value depending on the accuracy and training speed.

The trained model Mdl stores the bin edges in the BinEdges property.

Example: 'NumBins',50

Data Types: single | double

Number of trees per interaction term, specified as a positive integer scalar.

The 'NumTreesPerInteraction' value is equivalent to the number of gradient boosting iterations for the interaction terms for predictors. For each iteration, fitcgam adds a set of interaction trees to the model, one tree for each interaction term. To learn about the gradient boosting algorithm, see Gradient Boosting Algorithm.

You can determine whether the fitted model has the specified number of trees by viewing the diagnostic message displayed when 'Verbose' is 1 or 2, or by checking the ReasonForTermination property value of the model Mdl.

Example: 'NumTreesPerInteraction',500

Data Types: single | double

Number of trees per linear term, specified as a positive integer scalar.

The 'NumTreesPerPredictor' value is equivalent to the number of gradient boosting iterations for the linear terms for predictors. For each iteration, fitcgam adds a set of predictor trees to the model, one tree for each predictor. To learn about the gradient boosting algorithm, see Gradient Boosting Algorithm.

You can determine whether the fitted model has the specified number of trees by viewing the diagnostic message displayed when 'Verbose' is 1 or 2, or by checking the ReasonForTermination property value of the model Mdl.

Example: 'NumTreesPerPredictor',500

Data Types: single | double

Other Classification Options

collapse all

Categorical predictors list, specified as one of the values in this table.

ValueDescription
Vector of positive integers

Each entry in the vector is an index value indicating that the corresponding predictor is categorical. The index values are between 1 and p, where p is the number of predictors used to train the model.

If fitcgam uses a subset of input variables as predictors, then the function indexes the predictors using only the subset. The CategoricalPredictors values do not count any response variable, observation weights variable, or other variable that the function does not use.

Logical vector

A true entry means that the corresponding predictor is categorical. The length of the vector is p.

Character matrixEach row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length.
String array or cell array of character vectorsEach element in the array is the name of a predictor variable. The names must match the entries in PredictorNames.
"all"All predictors are categorical.

By default, if the predictor data is a table (Tbl), fitcgam assumes that a variable is categorical if it is a logical vector, unordered categorical vector, character array, string array, or cell array of character vectors. If the predictor data is a matrix (X), fitcgam assumes that all predictors are continuous. To identify any other predictors as categorical predictors, specify them by using the CategoricalPredictors name-value argument.

Example: 'CategoricalPredictors','all'

Data Types: single | double | logical | char | string | cell

Names of classes to use for training, specified as a categorical, character, or string array; a logical or numeric vector; or a cell array of character vectors. ClassNames must have the same data type as the response variable in Tbl or Y.

If ClassNames is a character array, then each element must correspond to one row of the array.

Use ClassNames to:

  • Specify the order of the classes during training.

  • Specify the order of any input or output argument dimension that corresponds to the class order. For example, use ClassNames to specify the order of the dimensions of Cost or the column order of classification scores returned by predict.

  • Select a subset of classes for training. For example, suppose that the set of all distinct class names in Y is ["a","b","c"]. To train the model using observations from classes "a" and "c" only, specify "ClassNames",["a","c"].

The default value for ClassNames is the set of all distinct class names in the response variable in Tbl or Y.

Example: "ClassNames",["b","g"]

Data Types: categorical | char | string | logical | single | double | cell

Misclassification cost of a point, specified as one of the following:

  • 2-by-2 numeric matrix, where Cost(i,j) is the cost of classifying a point into class j if its true class is i (that is, the rows correspond to the true class and the columns correspond to the predicted class). To specify the class order for the corresponding rows and columns of Cost, set the 'ClassNames' name-value argument.

  • Structure S with two fields: S.ClassNames, which contains the group names as a variable of the same data type as the response variable in Tbl or Y; and S.ClassificationCosts, which contains the cost matrix.

Example: 'Cost',[0 2; 1 0]

Data Types: single | double | struct

Number of iterations between diagnostic message printouts, specified as a nonnegative integer scalar. This argument is valid only when you specify 'Verbose' as 1.

If you specify 'Verbose',1 and 'NumPrint',numPrint, then the software displays diagnostic messages every numPrint iterations in the Command Window.

Example: 'NumPrint',500

Data Types: single | double

Predictor variable names, specified as a string array of unique names or cell array of unique character vectors. The functionality of PredictorNames depends on the way you supply the training data.

  • If you supply X and Y, then you can use PredictorNames to assign names to the predictor variables in X.

    • The order of the names in PredictorNames must correspond to the column order of X. That is, PredictorNames{1} is the name of X(:,1), PredictorNames{2} is the name of X(:,2), and so on. Also, size(X,2) and numel(PredictorNames) must be equal.

    • By default, PredictorNames is {'x1','x2',...}.

  • If you supply Tbl, then you can use PredictorNames to choose which predictor variables to use in training. That is, fitcgam uses only the predictor variables in PredictorNames and the response variable during training.

    • PredictorNames must be a subset of Tbl.Properties.VariableNames and cannot include the name of the response variable.

    • By default, PredictorNames contains the names of all predictor variables.

    • A good practice is to specify the predictors for training using either PredictorNames or formula, but not both.

Example: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]

Data Types: string | cell

Prior probabilities for each class, specified as one of the following:

  • Character vector or string scalar.

    • 'empirical' determines class probabilities from class frequencies in the response variable in Y or Tbl. If you pass observation weights, fitcgam uses the weights to compute the class probabilities.

    • 'uniform' sets all class probabilities to be equal.

  • Vector (one scalar value for each class). To specify the class order for the corresponding elements of 'Prior', set the 'ClassNames' name-value argument.

  • Structure S with two fields.

    • S.ClassNames contains the class names as a variable of the same type as the response variable in Y or Tbl.

    • S.ClassProbs contains a vector of corresponding probabilities.

fitcgam normalizes the weights in each class ('Weights') to add up to the value of the prior probability of the respective class.

Example: 'Prior','uniform'

Data Types: char | string | single | double | struct

Response variable name, specified as a character vector or string scalar.

  • If you supply Y, then you can use ResponseName to specify a name for the response variable.

  • If you supply ResponseVarName or formula, then you cannot use ResponseName.

Example: ResponseName="response"

Data Types: char | string

Score transformation, specified as a built-in transformation function name or function handle.

This table summarizes the available score transformations. Specify one using its corresponding character vector or string scalar.

ValueDescription
"doublelogit"1/(1 + e–2x)
"invlogit"log(x / (1 – x))
"ismax"Sets the score for the class with the largest score to 1, and sets the scores for all other classes to 0
"logit"1/(1 + e–x)
"none" or "identity"x (no transformation)
"sign"–1 for x < 0
0 for x = 0
1 for x > 0
"symmetric"2x – 1
"symmetricismax"Sets the score for the class with the largest score to 1, and sets the scores for all other classes to –1
"symmetriclogit"2/(1 + e–x) – 1

For a MATLAB function or a function you define, use its function handle for the score transform. The function handle must accept a matrix (the original scores) and return a matrix of the same size (the transformed scores).

This argument determines the output score computation for object functions such as predict, margin, and edge. Use 'logit' (default) to compute posterior probabilities, and use 'none' to compute the logit of posterior probabilities.

Example: 'ScoreTransform','none'

Data Types: char | string | function_handle

Verbosity level, specified as 0, 1, or 2. The Verbose value controls the amount of information that the software displays in the Command Window.

This table summarizes the available verbosity level options.

ValueDescription
0The software displays no information.
1The software displays diagnostic messages every numPrint iterations, where numPrint is the 'NumPrint' value.
2The software displays diagnostic messages at every iteration.

Each line of the diagnostic messages shows the information about each boosting iteration and includes the following columns:

  • Type — Type of trained trees, 1D (predictor trees, or boosted trees for linear terms for predictors) or 2D (interaction trees, or boosted trees for interaction terms for predictors)

  • NumTrees — Number of trees per linear term or interaction term that fitcgam added to the model so far

  • Deviance — Deviance of the model

  • RelTol — Relative change of model predictions: (y^k−y^k−1)′(y^k−y^k−1)/y^k′y^k, where y^k is a column vector of model predictions at iteration k

  • LearnRate — Learning rate used for the current iteration

Example: 'Verbose',1

Data Types: single | double

Observation weights, specified as a vector of scalar values or the name of a variable in Tbl. The software weights the observations in each row of X or Tbl with the corresponding value in Weights. The size of Weights must equal the number of rows in X or Tbl.

If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if the weights vector W is stored in Tbl.W, then specify it as 'W'.

fitcgam normalizes the weights in each class to add up to the value of the prior probability of the respective class.

Data Types: single | double | char | string

Note

You cannot use any cross-validation name-value argument together with the OptimizeHyperparameters name-value argument. You can modify the cross-validation for OptimizeHyperparameters only by using the HyperparameterOptimizationOptions name-value argument.

Cross-Validation Options

collapse all

Flag to train a cross-validated model, specified as 'on' or 'off'.

If you specify 'on', then the software trains a cross-validated model with 10 folds.

You can override this cross-validation setting using the 'CVPartition', 'Holdout', 'KFold', or 'Leaveout' name-value argument. You can use only one cross-validation name-value argument at a time to create a cross-validated model.

Alternatively, cross-validate after creating a model by passing Mdl to crossval.

Example: 'Crossval','on'

Cross-validation partition, specified as a cvpartition object that specifies the type of cross-validation and the indexing for the training and validation sets.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: Suppose you create a random partition for 5-fold cross-validation on 500 observations by using cvp = cvpartition(500,KFold=5). Then, you can specify the cross-validation partition by setting CVPartition=cvp.

Fraction of the data used for holdout validation, specified as a scalar value in the range (0,1). If you specify Holdout=p, then the software completes these steps:

  1. Randomly select and reserve p*100% of the data as validation data, and train the model using the rest of the data.

  2. Store the compact trained model in the Trained property of the cross-validated model.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: Holdout=0.1

Data Types: double | single

Number of folds to use in the cross-validated model, specified as a positive integer value greater than 1. If you specify KFold=k, then the software completes these steps:

  1. Randomly partition the data into k sets.

  2. For each set, reserve the set as validation data, and train the model using the other k – 1 sets.

  3. Store the k compact trained models in a k-by-1 cell vector in the Trained property of the cross-validated model.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: KFold=5

Data Types: single | double

Leave-one-out cross-validation flag, specified as "on" or "off". If you specify Leaveout="on", then for each of the n observations (where n is the number of observations, excluding missing observations, specified in the NumObservations property of the model), the software completes these steps:

  1. Reserve the one observation as validation data, and train the model using the other n – 1 observations.

  2. Store the n compact trained models in an n-by-1 cell vector in the Trained property of the cross-validated model.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: Leaveout="on"

Data Types: char | string

Hyperparameter Optimization Options

collapse all

Parameters to optimize, specified as one of these values:

  • 'none' — Do not optimize.

  • 'auto' — Optimize InitialLearnRateForPredictors, NumTreesPerPredictor, Interactions, InitialLearnRateForInteractions, and NumTreesPerInteraction.

  • 'auto-univariate' — Optimize InitialLearnRateForPredictors and NumTreesPerPredictor.

  • 'auto-bivariate' — Optimize Interactions, InitialLearnRateForInteractions, and NumTreesPerInteraction.

  • 'all' — Optimize all eligible parameters.

  • 'all-univariate' — Optimize all eligible univariate parameters.

  • 'all-bivariate' — Optimize all eligible bivariate parameters.

  • String array or cell array of eligible parameter names.

  • Vector of optimizableVariable objects, typically the output of hyperparameters.

The eligible parameters for fitcgam are:

  • Univariate hyperparameters

    • InitialLearnRateForPredictors — fitcgam searches among real values, log-scaled in the range [1e-3,1].

    • MaxNumSplitsPerPredictor — fitcgam searches among integers in the range [1,maxNumSplits], where maxNumSplits is min(30,max(2,NumObservations–1)). NumObservations is the number of observations, excluding missing observations, stored in the NumObservations property of the returned model Mdl.

    • NumTreesPerPredictor — fitcgam searches among integers, log-scaled in the range [10,500].

  • Bivariate hyperparameters

    • Interactions — fitcgam searches among integers, log-scaled in the range [0,MaxNumInteractions]t, where MaxNumInteractions is NumPredictors*(NumPredictors – 1)/2, and NumPredictors is the number of predictors used to train the model.

    • InitialLearnRateForInteractions — fitcgam searches among real values, log-scaled in the range [1e-3,1].

    • MaxNumSplitsPerInteraction — fitcgam searches among integers in the range [1,maxNumSplits].

    • NumTreesPerInteraction — fitcgam searches among integers, log-scaled in the range [10,500].

Use 'auto' or 'all' to find optimal hyperparameter values for both univariate and bivariate parameters. Alternatively, you can find optimal values for univariate parameters using 'auto-univariate' or 'all-univariate' and then find optimal values for bivariate parameters using 'auto-bivariate' or 'all-bivariate'. For examples, see Optimize GAM Using OptimizeHyperparameters and Train Generalized Additive Model for Binary Classification.

The optimization attempts to minimize the cross-validation loss (error) for fitcgam by varying the parameters. To control the cross-validation type and other aspects of the optimization, use the HyperparameterOptimizationOptions name-value argument. When you use HyperparameterOptimizationOptions, you can use the (compact) model size instead of the cross-validation loss as the optimization objective by setting the ConstraintType and ConstraintBounds options.

Note

The values of OptimizeHyperparameters override any values you specify using other name-value arguments. For example, setting OptimizeHyperparameters to "auto" causes fitcgam to optimize hyperparameters corresponding to the "auto" option and to ignore any specified values for the hyperparameters.

Set nondefault parameters by passing a vector of optimizableVariable objects that have nondefault values. For example:

load fisheriris
params = hyperparameters('fitcgam',meas,species);
params(1).Range = [1e-4,1e6];

Pass params as the value of OptimizeHyperparameters.

By default, the iterative display appears at the command line, and plots appear according to the number of hyperparameters in the optimization. For the optimization and plots, the objective function is the misclassification rate. To control the iterative display, set the Verbose option of the HyperparameterOptimizationOptions name-value argument. To control the plots, set the ShowPlots field of the HyperparameterOptimizationOptions name-value argument.

Example: 'OptimizeHyperparameters','auto'

Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. This argument modifies the effect of the OptimizeHyperparameters name-value argument. If you specify HyperparameterOptimizationOptions, you must also specify OptimizeHyperparameters. All the options are optional. However, you must set ConstraintBounds and ConstraintType to return AggregateOptimizationResults. The options that you can set in a structure are the same as those in the HyperparameterOptimizationOptions object.

OptionValuesDefault
Optimizer

  • "bayesopt" — Use Bayesian optimization. Internally, this setting calls bayesopt.

  • "gridsearch" — Use grid search with NumGridDivisions values per dimension. "gridsearch" searches in a random order, using uniform sampling without replacement from the grid. After optimization, you can get a table in grid order by using the command sortrows(Mdl.HyperparameterOptimizationResults).

  • "randomsearch" — Search at random among MaxObjectiveEvaluations points.

"bayesopt"
ConstraintBounds

Constraint bounds for N optimization problems, specified as an N-by-2 numeric matrix or []. The columns of ConstraintBounds contain the lower and upper bound values of the optimization problems. If you specify ConstraintBounds as a numeric vector, the software assigns the values to the second column of ConstraintBounds, and zeros to the first column. If you specify ConstraintBounds, you must also specify ConstraintType.

[]
ConstraintTarget

Constraint target for the optimization problems, specified as "matlab" or "coder". If ConstraintBounds and ConstraintType are [] and you set ConstraintTarget, then the software sets ConstraintTarget to []. The values of ConstraintTarget and ConstraintType determine the objective and constraint functions. For more information, see HyperparameterOptimizationOptions.

If you specify ConstraintBounds and ConstraintType, then the default value is "matlab". Otherwise, the default value is [].
ConstraintType

Constraint type for the optimization problems, specified as "size" or "loss". If you specify ConstraintType, you must also specify ConstraintBounds. The values of ConstraintTarget and ConstraintType determine the objective and constraint functions. For more information, see HyperparameterOptimizationOptions.

[]
AcquisitionFunctionName

Type of acquisition function:

  • "expected-improvement-per-second-plus"

  • "expected-improvement"

  • "expected-improvement-plus"

  • "expected-improvement-per-second"

  • "lower-confidence-bound"

  • "probability-of-improvement"

Acquisition functions whose names include per-second do not yield reproducible results, because the optimization depends on the run time of the objective function. Acquisition functions whose names include plus modify their behavior when they overexploit an area. For more details, see Acquisition Function Types.

"expected-improvement-per-second-plus"
MaxObjectiveEvaluationsMaximum number of objective function evaluations. If you specify multiple optimization problems using ConstraintBounds, the value of MaxObjectiveEvaluations applies to each optimization problem individually.30 for "bayesopt" and "randomsearch", and the entire grid for "gridsearch"
MaxTime

Time limit for the optimization, specified as a nonnegative real scalar. The time limit is in seconds, as measured by tic and toc. The software performs at least one optimization iteration, regardless of the value of MaxTime. The run time can exceed MaxTime because MaxTime does not interrupt function evaluations. If you specify multiple optimization problems using ConstraintBounds, the time limit applies to each optimization problem individually.

Inf
NumGridDivisionsFor Optimizer="gridsearch", the number of values in each dimension. The value can be a vector of positive integers giving the number of values for each dimension, or a scalar that applies to all dimensions. This option is ignored for categorical variables.10
ShowPlotsLogical value indicating whether to show plots of the optimization progress. If this option is true, the software plots the best observed objective function value against the iteration number. If you use Bayesian optimization (Optimizer="bayesopt"), then the software also plots the best estimated objective function value. The best observed objective function values and best estimated objective function values correspond to the values in the BestSoFar (observed) and BestSoFar (estim.) columns of the iterative display, respectively. You can find these values in the properties ObjectiveMinimumTrace and EstimatedObjectiveMinimumTrace of Mdl.HyperparameterOptimizationResults. If the problem includes one or two optimization parameters for Bayesian optimization, then ShowPlots also plots a model of the objective function against the parameters.true
SaveIntermediateResultsLogical value indicating whether to save the optimization results. If this option is true, the software overwrites a workspace variable named "BayesoptResults" at each iteration. The variable is a BayesianOptimization object. If you specify multiple optimization problems using ConstraintBounds, the workspace variable is an AggregateBayesianOptimization object named "AggregateBayesoptResults".false
Verbose

Display level at the command line:

  • 0 — No iterative display

  • 1 — Iterative display

  • 2 — Iterative display with additional information

For details, see the bayesopt Verbose name-value argument and the example Optimize Classifier Fit Using Bayesian Optimization.

1
UseParallelLogical value indicating whether to run the Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization.false
Repartition

Logical value indicating whether to repartition the cross-validation at every iteration. If this option is false, the optimizer uses a single partition for the optimization.

A value of true usually gives the most robust results because this setting takes partitioning noise into account. However, for optimal results, true requires at least twice as many function evaluations.

false
Specify only one of the following three options.
CVPartitioncvpartition object created by cvpartitionKfold=5 if you do not specify a cross-validation option
HoldoutScalar in the range (0,1) representing the holdout fraction
KfoldInteger greater than 1

Example: HyperparameterOptimizationOptions=struct(UseParallel=true)

Output Arguments

collapse all

Trained generalized additive model, returned as one of the model objects in this table.

Model ObjectCross-Validation Options to Train Model ObjectWays to Classify Observations Using Model Object
ClassificationGAMNoneUse predict to classify new observations, and use resubPredict to classify training observations.
ClassificationPartitionedGAMSpecify KFold, Holdout, Leaveout, CrossVal, or CVPartitionUse kfoldPredict to classify observations that fitcgam holds out during training. kfoldPredict predicts a class label for every observation by using the model trained without that observation.

To reference properties of Mdl, use dot notation. For example, enter Mdl.Interactions in the Command Window to display the interaction terms in Mdl.

If you specify OptimizeHyperparameters and set the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions, then Mdl is an N-by-1 cell array of model objects, where N is equal to the number of rows in ConstraintBounds. If none of the optimization problems yields a feasible model, then each cell array value is [].

Aggregate optimization results for multiple optimization problems, returned as an AggregateBayesianOptimization object. To return AggregateOptimizationResults, you must specify OptimizeHyperparameters and HyperparameterOptimizationOptions. You must also specify the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions. For an example that shows how to produce this output, see Hyperparameter Optimization with Multiple Constraint Bounds.

More About

collapse all

Generalized Additive Model (GAM) for Binary Classification

A generalized additive model (GAM) is an interpretable model that explains class scores (the logit of class probabilities) using a sum of univariate and bivariate shape functions of predictors.

fitcgam uses a boosted tree as a shape function for each predictor and, optionally, each pair of predictors; therefore, the function can capture a nonlinear relation between a predictor and the response variable. Because contributions of individual shape functions to the prediction (classification score) are well separated, the model is easy to interpret.

The standard GAM uses a univariate shape function for each predictor.

y~Binomial(n,μ)g(μ)=logμ1−μ=c+​f1(x1)+​f2(x2)+⋯+fp(xp),

where y is a response variable that follows the binomial distribution with the probability of success (probability of positive class) μ in n observations. g(μ) is a logit link function, and c is an intercept (constant) term. fi(xi) is a univariate shape function for the ith predictor, which is a boosted tree for a linear term for the predictor (predictor tree).

You can include interactions between predictors in a model by adding bivariate shape functions of important interaction terms to the model.

g(μ)=c+​f1(x1)+​f2(x2)+⋯+fp(xp)+∑i,j∈{1,2,⋯,p}fij(xixj),

where fij(xixj) is a bivariate shape function for the ith and jth predictors, which is a boosted tree for an interaction term for the predictors (interaction tree).

fitcgam finds important interaction terms based on the p-values of F-tests. For details, see Interaction Term Detection.

Deviance

Deviance is a generalization of the residual sum of squares. It measures the goodness of fit compared to the saturated model.

The deviance of a fitted model is twice the difference between the loglikelihoods of the model and the saturated model:

-2(logL - logLs),

where L and Ls are the likelihoods of the fitted model and the saturated model, respectively. The saturated model is the model with the maximum number of parameters that you can estimate.

fitcgam uses the deviance to measure the goodness of model fit and finds a learning rate that reduces the deviance at each iteration. Specify 'Verbose' as 1 or 2 to display the deviance and learning rate in the Command Window.

Algorithms

collapse all

Gradient Boosting Algorithm

fitcgam fits a generalized additive model using a gradient boosting algorithm (Adaptive Logistic Regression).

fitcgam first builds sets of predictor trees (boosted trees for linear terms for predictors) and then builds sets of interaction trees (boosted trees for interaction terms for predictors). The boosting algorithm iterates for at most 'NumTreesPerPredictor' times for predictor trees, and then iterates for at most 'NumTreesPerInteraction' times for interaction trees.

For each boosting iteration, fitcgam builds a set of predictor trees with the initial learning rate 'InitialLearnRateForPredictors', or builds a set of interaction trees with the initial learning rate 'InitialLearnRateForInteractions'.

  • When building a set of trees, the function trains one tree at a time. It fits a tree to the residual that is the difference between the response and the aggregated prediction from all trees grown previously. To control the boosting learning speed, the function shrinks the tree by the learning rate and then adds the tree to the model and updates the residual.

    • Updated model = current model + (learning rate)·(new tree)

    • Updated residual = current residual – (learning rate)·(response explained by new tree)

  • If adding the set of trees improves the model fit (that is, reduces the deviance of the fit by a value larger than a tolerance), then fitcgam moves to the next iteration.

  • Otherwise, fitcgam halves the learning rate and uses it to update the model and residual. The function continues to halve the learning rate until it finds a rate that improves the model fit.

    • If the function cannot find such a learning rate when training predictor trees, then it stops boosting iterations for linear terms and starts boosting iterations for interaction terms.

    • If the function cannot find such a learning rate when training interaction trees, then it terminates the model fitting.

    You can determine why training stopped by checking the ReasonForTermination property of the trained model.

Interaction Term Detection

For each pairwise interaction term xixj (specified by formula or 'Interactions'), the software performs an F-test to examine whether the term is statistically significant.

To speed up the process, fitcgam bins numeric predictors into at most 8 equiprobable bins. The number of bins can be less than 8 if a predictor has fewer than 8 unique values. The F-test examines the null hypothesis that the bins created by xi and xj have equal responses versus the alternative that at least one bin has a different response value from the others. A small p-value indicates that differences are significant, which implies that the corresponding interaction term is significant and, therefore, including the term can improve the model fit.

fitcgam builds a set of interaction trees using the terms whose p-values are not greater than the 'MaxPValue' value. You can use the default 'MaxPValue' value 1 to build interaction trees using all terms specified by formula or 'Interactions'.

fitcgam adds interaction terms to the model in the order of importance based on the p-values. Use the Interactions property of the returned model to check the order of the interaction terms added to the model.

Cost, Prior, and Weights

  • If you specify the Cost, Prior, and Weights name-value arguments, the output model object stores the specified values in the Cost, Prior, and W properties, respectively. The Cost property stores the user-specified cost matrix as is. The Prior and W properties store the prior probabilities and observation weights, respectively, after normalization. For details, see Misclassification Cost Matrix, Prior Probabilities, and Observation Weights.

  • The software uses the Cost property for prediction, but not training. Therefore, Cost is not read-only; you can change the property value by using dot notation after creating the trained model.

References

[1] Lou, Yin, Rich Caruana, and Johannes Gehrke. "Intelligible Models for Classification and Regression." Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’12). Beijing, China: ACM Press, 2012, pp. 150–158.

[2] Lou, Yin, Rich Caruana, Johannes Gehrke, and Giles Hooker. "Accurate Intelligible Models with Pairwise Interactions." Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’13) Chicago, Illinois, USA: ACM Press, 2013, pp. 623–631.

Extended Capabilities

Version History

Introduced in R2021a

See Also

| | | |

Topics