Main Content

fit

Compute Shapley values for query points

Since R2021a

collapse all in page

    Syntax

    newExplainer = fit(explainer,queryPoints)
    newExplainer = fit(explainer,queryPoints,Name=Value)

    Description

    newExplainer = fit(explainer,queryPoints) computes the Shapley values for the specified query points (queryPoints) and stores the computed Shapley values in the Shapley property of newExplainer. The shapley object explainer contains a machine learning model and the options for computing Shapley values.

    fit uses the Shapley value computation options that you specify when you create explainer. You can change the options using the name-value arguments of the fit function. The function returns a shapley object newExplainer that contains the newly computed Shapley values.

    example

    newExplainer = fit(explainer,queryPoints,Name=Value) specifies additional options using one or more name-value arguments. For example, specify UseParallel=true to compute Shapley values in parallel.

    example

    Examples

    collapse all

    Open Live Script

    Train a regression model and create a shapley object. When you create a shapley object, if you do not specify query points, then the software does not compute Shapley values. Use the object function fit to compute the Shapley values for a specified query point. Then create a bar graph of the Shapley values by using the object function plot.

    Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s.

    load carbig

    Create a table containing the predictor variables Acceleration, Cylinders, and so on, as well as the response variable MPG.

    tbl = table(Acceleration,Cylinders,Displacement, ...
    Horsepower,Model_Year,Weight,MPG);

    Removing missing values in a training set can help reduce memory consumption and speed up training for the fitrkernel function. Remove missing values in tbl. 

    tbl = rmmissing(tbl);

    Train a blackbox model of MPG by using the fitrkernel function. Specify the Cylinders and Model_Year variables as categorical predictors. Standardize the remaining predictors.

    rng("default") % For reproducibility
mdl = fitrkernel(tbl,"MPG",CategoricalPredictors=[2 5], ...
    Standardize=true);

    Create a shapley object. Specify the data set tbl, because mdl does not contain training data.

    explainer = shapley(mdl,tbl)
    explainer = 
            BlackboxModel: [1×1 RegressionKernel]
              QueryPoints: []
           BlackboxFitted: []
                  Shapley: []
                        X: [392×7 table]
    CategoricalPredictors: [2 5]
                   Method: "interventional-kernel"
                Intercept: 23.2474
               NumSubsets: 64

    explainer stores the training data tbl in the X property. By default, shapley subsamples 100 observations from the data in X and stores their indices in the SampledObservationIndices property.

    Compute the Shapley values of all predictor variables for the first observation in tbl. The fit object function uses the sampled observations rather than all of X to compute the Shapley values.

    queryPoint = tbl(1,:)
    queryPoint=1×7 table
    Acceleration    Cylinders    Displacement    Horsepower    Model_Year    Weight    MPG
    ____________    _________    ____________    __________    __________    ______    ___

         12             8            307            130            70         3504     18 


    explainer = fit(explainer,queryPoint);

    For a regression model, fit computes Shapley values using the predicted response, and stores them in the Shapley property of the shapley object. Display the values in the Shapley property.

    explainer.Shapley
    ans=6×2 table
      Predictor        Value  
    ______________    ________

    "Acceleration"    -0.33821
    "Cylinders"       -0.97631
    "Displacement"     -1.1425
    "Horsepower"      -0.62927
    "Model_Year"      -0.17268
    "Weight"          -0.87595

    Plot the Shapley values for the query point by using the plot function.

    plot(explainer)

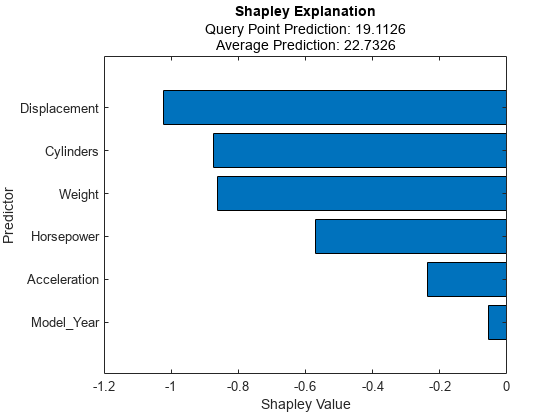
    Figure contains an axes object. The axes object with title Shapley Explanation, xlabel Shapley Value, ylabel Predictor contains an object of type bar.

    The horizontal bar graph shows the Shapley values for all variables, sorted by their absolute values. Each Shapley value explains the deviation of the prediction for the query point from the average, due to the corresponding variable.

    Open Live Script

    Train a classification model and create a shapley object. Then compute the Shapley values for two query points.

    Load the CreditRating_Historical data set. The data set contains customer IDs and their financial ratios, industry labels, and credit ratings.

    tbl = readtable("CreditRating_Historical.dat");

    Train a blackbox model of credit ratings by using the fitcecoc function. Use the variables from the second through seventh columns in tbl as the predictor variables.

    blackbox = fitcecoc(tbl,"Rating", ...
    PredictorNames=tbl.Properties.VariableNames(2:7), ...
    CategoricalPredictors="Industry");

    Create a shapley object with the blackbox model. Specify to sample 1000 observations from tbl to compute the Shapley values. Specify to use the extension to the Kernel SHAP algorithm.

    rng("default") % For reproducibility
explainer = shapley(blackbox,tbl,Method="conditional", ...
    NumObservationsToSample=1000);

    Find two query points whose true rating values are AAA and BB, respectively.

    sampleTbl = explainer.X(explainer.SampledObservationIndices,:);
queryPoints(1,:) = sampleTbl(find(strcmp(sampleTbl.Rating,"AAA"),1),:);
queryPoints(2,:) = sampleTbl(find(strcmp(sampleTbl.Rating,"BB"),1),:)
    queryPoints=2×8 table
     ID      WC_TA    RE_TA    EBIT_TA    MVE_BVTD    S_TA     Industry    Rating 
    _____    _____    _____    _______    ________    _____    ________    _______

    39364     0.61    0.694     0.122      5.409      0.359       3        {'AAA'}
    44610    0.254    0.226     0.064      0.779      0.254       5        {'BB' }

    Compute and plot the Shapley values for the first query point.

    explainer1 = fit(explainer,queryPoints(1,:));
plot(explainer1)

    Figure contains an axes object. The axes object with title Shapley Explanation, xlabel Shapley Value, ylabel Predictor contains an object of type bar.

    Compute and plot the Shapley values for the second query point.

    explainer2 = fit(explainer,queryPoints(2,:));
plot(explainer2)

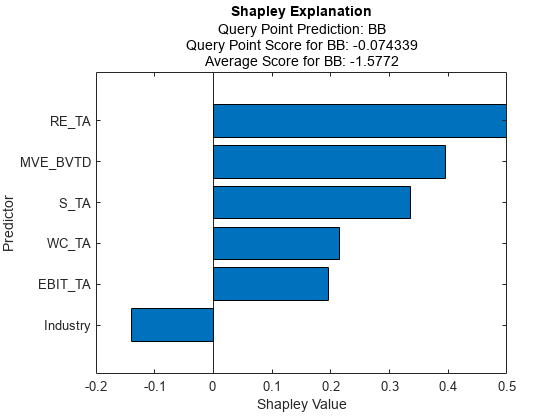
    Figure contains an axes object. The axes object with title Shapley Explanation, xlabel Shapley Value, ylabel Predictor contains an object of type bar.

    The true rating for the second query point is BB, but the predicted rating is BBB. The plot shows the Shapley values for the predicted rating.

    explainer1 and explainer2 include the Shapley values for the first query point and second query point, respectively.

    This example uses:

    Open Live Script

    Train a regression model and create a shapley object. Use the object function fit to compute the Shapley values for the specified query points. Then plot the Shapley values for multiple query points by using the swarmchart object function.

    Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s.

    load carbig

    Create a table containing the predictor variables Acceleration, Cylinders, and so on, as well as the response variable MPG.

    tbl = table(Acceleration,Cylinders,Displacement, ...
    Horsepower,Model_Year,Weight,MPG);

    Removing missing values in a training set helps to reduce memory consumption and speed up training for the fitrkernel function. Remove missing values in tbl.

    tbl = rmmissing(tbl);

    Train a blackbox model of MPG by using the fitrkernel function. Specify the Cylinders and Model_Year variables as categorical predictors. Standardize the remaining predictors.

    rng("default") % For reproducibility
mdl = fitrkernel(tbl,"MPG",CategoricalPredictors=[2 5], ...
    Standardize=true);

    Create a shapley object. Because mdl does not contain training data, specify the data set tbl.

    explainer = shapley(mdl,tbl)
    explainer = 
            BlackboxModel: [1×1 RegressionKernel]
              QueryPoints: []
           BlackboxFitted: []
                  Shapley: []
                        X: [392×7 table]
    CategoricalPredictors: [2 5]
                   Method: "interventional-kernel"
                Intercept: 23.2474
               NumSubsets: 64

    explainer stores the training data tbl in the X property. By default, shapley subsamples 100 observations from the data in X and stores their indices in the SampledObservationIndices property.

    Compute the Shapley values for all observations in tbl. To speed up computations, the fit object function uses the sampled observations rather than all of X to compute the Shapley values. Further reduce computational time by using the UseParallel name-value argument, if you have a Parallel Computing Toolbox™ license.

    explainer = fit(explainer,tbl,UseParallel=true);

    For a regression model, fit computes Shapley values using the predicted response, and stores them in the Shapley property of the shapley object. Because explainer contains Shapley values for multiple query points, display the mean absolute Shapley values instead.

    explainer.MeanAbsoluteShapley
    ans=6×2 table
      Predictor        Value 
    ______________    _______

    "Acceleration"     0.5678
    "Cylinders"       0.96799
    "Displacement"    0.79668
    "Horsepower"      0.78681
    "Model_Year"      0.86258
    "Weight"            0.987

    For each predictor, the mean absolute Shapley value is the absolute value of the Shapley values, averaged across all query points. The Cylinders predictor has the greatest mean absolute Shapley value, and the Acceleration predictor has the smallest mean absolute Shapley value.

    Visualize the Shapley values by using the swarmchart object function. Specify to use the "copper" colormap.

    swarmchart(explainer,ColorMap="copper")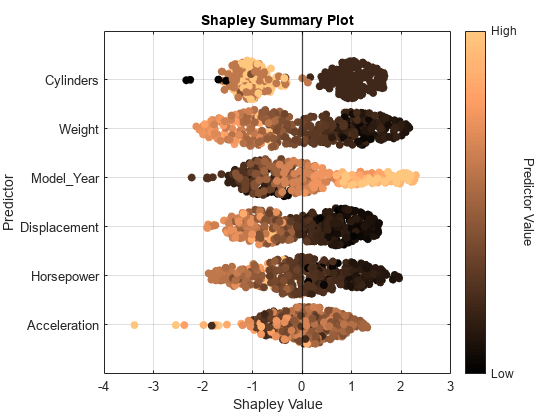

    Figure contains an axes object. The axes object with title Shapley Summary Plot, xlabel Shapley Value, ylabel Predictor contains 7 objects of type constantline, scatter.

    For each predictor, the function displays the Shapley values for the query points. The corresponding swarm chart shows the distribution of the Shapley values. The function determines the order of the predictors by using the mean absolute Shapley values.

    Query points with low Weight values seem to have large positive Shapley values. That is, for these query points, the Weight predictor contributes to an increase in the MPG predicted value from the average. Similarly, query points with high Weight values seem to have large negative Shapley values. That is, for these query points, the Weight predictor contributes to a decrease in the MPG predicted value from the average. These results match the idea that car weights are inversely correlated with MPG values.

    Input Arguments

    collapse all

    Object explaining the blackbox model, specified as a shapley object.

    Query points at which fit explains predictions, specified as a numeric matrix or a table. Each row of queryPoints corresponds to one query point.

    • For a numeric matrix:

      • The variables that make up the columns of queryPoints must have the same order as the predictor data X in explainer.

      • If the predictor data explainer.X is a table, then queryPoints can be a numeric matrix if the table contains all numeric variables.

    • For a table:

      • If the predictor data explainer.X is a table, then all predictor variables in queryPoints must have the same variable names and data types as those in explainer.X. However, the column order of queryPoints does not need to correspond to the column order of explainer.X.

      • If the predictor data explainer.X is a numeric matrix, then the predictor names in explainer.BlackboxModel.PredictorNames and the corresponding predictor variable names in queryPoints must be the same. To specify predictor names during training, use the PredictorNames name-value argument. All predictor variables in queryPoints must be numeric vectors.

      • queryPoints can contain additional variables (response variables, observation weights, and so on), but fit ignores them.

      • fit does not support multicolumn variables or cell arrays other than cell arrays of character vectors.

    If queryPoints contains NaNs for continuous predictors and Method is "conditional", then the Shapley values (Shapley) in the returned object are NaNs. If you use a regression model that is a Gaussian process regression (GPR), kernel, linear, neural network, or support vector machine (SVM) model, then fit returns NaN Shapley values for query points that contain missing predictor values or categories not seen during training. For all other models, fit handles missing values in the same way as explainer.BlackboxModel (that is, the predict object function of explainer.BlackboxModel or a function handle specified by blackbox).

    Before R2024a: You can specify only one query point using a row vector of numeric values or a single-row table.

    Example: explainer.X(1,:) specifies the query point as the first observation of the predictor data X in explainer.

    Data Types: single | double | table

    Name-Value Arguments

    Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

    Example: fit(explainer,q,Method="conditional",UseParallel=true) computes the Shapley values for the query point q using the extension to the Kernel SHAP algorithm, and executes the computation in parallel.

    Maximum number of predictor subsets to use for Shapley value computation, specified as a positive integer.

    For details on how fit chooses the subsets to use, see Computational Cost.

    This argument is valid when the fit function uses the Kernel SHAP algorithm or the extension to the Kernel SHAP algorithm. If you set the MaxNumSubsets argument when Method is "interventional", the software uses the Kernel SHAP algorithm. For more information, see Algorithms.

    Example: MaxNumSubsets=100

    Data Types: single | double

    Shapley value computation algorithm, specified as "interventional" or "conditional".

    • "interventional" — fit computes the Shapley values with an interventional value function.

      fit offers three interventional algorithms: Kernel SHAP [1], Linear SHAP [1], and Tree SHAP [2]. For each query point, the software selects an algorithm based on the machine learning model explainer.BlackboxModel and other specified options. For details, see Interventional Algorithms.

    • "conditional" — fit uses the extension to the Kernel SHAP algorithm [3] with a conditional value function.

    The Method property of newExplainer stores the name of the selected algorithm. For more information, see Algorithms.

    By default, the fit function uses the algorithm specified in the Method property of explainer.

    Before R2023a: You can specify this argument as "interventional-kernel" or "conditional-kernel". fit supports the Kernel SHAP algorithm and the extension of the Kernel SHAP algorithm.

    Example: Method="conditional"

    Data Types: char | string

    Since R2024a

    Function called after each query point evaluation, specified as a function handle. An output function can perform various tasks, such as stopping Shapley value computations, creating variables, or plotting results. For details and examples on how to write your own output functions, see Shapley Output Functions.

    This argument is valid only when the fit function computes Shapley values for multiple query points.

    Data Types: function_handle

    Flag to run in parallel, specified as a numeric or logical 1 (true) or 0 (false). If you specify UseParallel=true, the fit function executes for-loop iterations by using parfor. The loop runs in parallel when you have Parallel Computing Toolbox™.

    This argument is valid only when the fit function computes Shapley values for multiple query points, or computes Shapley values for one query point by using the Tree SHAP algorithm for an ensemble of trees, the Kernel SHAP algorithm, or the extension to the Kernel SHAP algorithm.

    Example: UseParallel=true

    Data Types: logical

    Output Arguments

    collapse all

    Object explaining the blackbox model, returned as a shapley object. The Shapley property of the object contains the computed Shapley values.

    To overwrite the input argument explainer, assign the output of fit to explainer:

    explainer = fit(explainer,queryPoints);

    More About

    collapse all

    Shapley Values

    In game theory, the Shapley value of a player is the average marginal contribution of the player in a cooperative game. In the context of machine learning prediction, the Shapley value of a feature for a query point explains the contribution of the feature to a prediction (response for regression or score of each class for classification) at the specified query point.

    The Shapley value of a feature for a query point is the contribution of the feature to the deviation from the average prediction. For a query point, the sum of the Shapley values for all features corresponds to the total deviation of the prediction from the average. That is, the sum of the average prediction and the Shapley values for all features corresponds to the prediction for the query point.

    For more details, see Shapley Values for Machine Learning Model.

    References

    [1] Lundberg, Scott M., and S. Lee. "A Unified Approach to Interpreting Model Predictions." Advances in Neural Information Processing Systems 30 (2017): 4765–774.

    [2] Lundberg, Scott M., G. Erion, H. Chen, et al. "From Local Explanations to Global Understanding with Explainable AI for Trees." Nature Machine Intelligence 2 (January 2020): 56–67.

    [3] Aas, Kjersti, Martin Jullum, and Anders Løland. "Explaining Individual Predictions When Features Are Dependent: More Accurate Approximations to Shapley Values." Artificial Intelligence 298 (September 2021).

    Extended Capabilities

    Version History

    Introduced in R2021a

    expand all

    See Also

    | | | |

    Topics