Main Content

directforecaster

Fit direct forecasting model

Since R2023b

expand all in page

    Description

    DirectForecaster is a multistep forecasting model that uses a direct strategy in which a separate regression model is trained for each step of the forecasting horizon. For more information, see Direct Forecasting. Use the directforecaster function to train a DirectForecaster model with regularly sampled time series data.

    You can use lagged and leading predictors to train the direct forecasting model. directforecaster creates the appropriate predictors when you specify the following:

    For more information, see Forecasting Data.

    After creating a DirectForecaster object, you can see how the model performs on observed test data by using the loss and predict object functions. You can then use the model to forecast at time steps beyond the available data by using the forecast object function.

    Creation

    Syntax

    Mdl = directforecaster(Tbl,ResponseVarName)
    Mdl = directforecaster(X,Y)
    Mdl = directforecaster(Y)
    Mdl = directforecaster(__,Name=Value)

    Description

    Mdl = directforecaster(Tbl,ResponseVarName) creates a direct forecasting model Mdl using the regularly sampled data in Tbl and the response in variable ResponseVarName in Tbl. The function treats all variables in Tbl other than ResponseVarName as exogenous predictor variables.

    By default, the resulting Mdl object contains one regression model, with a time horizon of one step ahead. directforecaster uses a lag value of 1 to create predictors from the exogenous predictors and the response variable.

    example

    Mdl = directforecaster(X,Y) creates a direct forecasting model using the exogenous predictor data X and the response data Y.

    Mdl = directforecaster(Y) creates a direct forecasting model using the response data Y. When you do not specify exogenous predictor data, the model uses only lagged response variables as predictors.

    Mdl = directforecaster(__,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. For example, you can create a model that forecasts at the first, third, and fifth horizon steps by specifying Horizon=[1 3 5].

    example

    Input Arguments

    expand all

    Training set data, specified as a table or timetable. Each row of Tbl corresponds to one observation, and each column corresponds to one variable. Tbl must contain the response variable ResponseVarName.

    • The software assumes that the observations in Tbl are regularly sampled. Ensure that no time steps are missing or duplicated and that the observations are in ascending order.

    • By default, the software treats all variables in Tbl other than ResponseVarName as exogenous predictors. To use a subset of the variables in Tbl as exogenous predictors during model training, specify the PredictorNames name-value argument.

    Response variable name, specified as the name of a variable in Tbl. The response variable must contain numeric values.

    You must specify ResponseVarName as a character vector or string scalar. For example, if Tbl stores the response variable Response as Tbl.Response, then specify it as "Response".

    Data Types: char | string

    Training set exogenous predictor data, specified as a numeric matrix, table, or timetable. Each row of X corresponds to one observation, and each column corresponds to one predictor.

    • The software assumes that the observations in X are regularly sampled. Ensure that no time steps are missing or duplicated and that the observations are in ascending order.

    • X and Y must have the same number of observations.

    • If X is a matrix, you can specify the names of the predictors in the order of their appearance in X by using the PredictorNames name-value argument.

    • If X is a table or timetable, you can use a subset of the variables in Tbl as exogenous predictors during model training by specifying the PredictorNames name-value argument.

    Training set response data, specified as a numeric vector, one-column table, or one-column timetable. Each row of Y corresponds to one observation.

    • If X is a numeric matrix, then Y must be a numeric vector.

    • If X is a table, then Y must be a numeric vector or one-column table.

    • If X is a timetable or it is not specified, then Y must be a numeric vector, one-column table, or one-column timetable.

    If you specify both X and Y, then they must have the same number of observations.

    Name-Value Arguments

    Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

    Example: directforecaster(Tbl,"Y",Horizon=1:3,LeadingPredictors="all",LeadingPredictorLags=0:1,ResponseLags=1:2) specifies to forecast at the first, second, and third horizon steps using lagged and leading predictors. The software treats all exogenous predictors as leading predictors, and creates one new lagged feature from each exogenous predictor in Tbl and two new lagged features from the response variable Y in Tbl. The leading predictor lag value of 0 specifies to also use the unshifted exogenous predictors.

    Future time steps at which to forecast, specified as a positive integer vector. The software uses each specified value in Horizon as a individual horizon step, and trains a regression model that forecasts at that horizon step.

    By default, the software trains one regression model that forecasts one step ahead.

    Example: Horizon=1:5

    Example: Horizon=[2 4 6]

    Data Types: single | double

    Type of regression model to train at each horizon step, specified as one of the values in this table.

    ValueRegression Model Type
    "bag" or templateEnsemble template (with the method specified as "Bag" and the weak learners specified as "Tree")Bagged ensemble of trees
    "gam" or templateGAM templateGeneral additive model (GAM)
    "gp" or templateGP templateGaussian process regression (GPR)
    "kernel" or templateKernel templateKernel model
    "linear" or templateLinear templateLinear model
    "lsboost" or templateEnsemble template (with the method specified as "LSBoost" and the weak learners specified as "Tree")Boosted ensemble of trees
    "svm" or templateSVM templateSupport vector machine (SVM)
    "tree" or templateTree templateDecision tree

    Example: Learner="svm"

    Example: Learner=templateEnsemble("LSBoost",50,"Tree")

    List of exogenous predictors whose future values are known, specified as one of the values in this table.

    ValueDescription
    Positive integer vector

    Each entry in the vector is an index value indicating that the corresponding exogenous predictor is leading. The index values are between 1 and p, where p is the number of exogenous predictors listed in PredictorNames.

    Logical vector

    A true entry means that the corresponding exogenous predictor is leading. The length of the vector is p.

    String array or cell array of character vectorsEach element in the array is the name of a leading exogenous predictor variable. The names must match the entries in PredictorNames.
    "all"All exogenous predictors are leading.

    Note

    This name-value argument is valid only when you use exogenous predictors.

    Example: LeadingPredictors="all"

    Data Types: single | double | logical | string | cell

    Predictor lags for preparing leading exogenous predictors, specified as a nonnegative integer vector or a 1-by-l cell array of nonnegative integer vectors, where l is the number of leading exogenous predictors.

    • If LeadingPredictorLags is a vector, then the software applies each specified lag value in LeadingPredictorLags to all the leading exogenous predictors. That is, for each element i in the vector, the software shifts the leading exogenous predictors backward in time by i steps, relative to the horizon time step. The software uses the resulting features as predictors.

    • If LeadingPredictorLags is a cell array, then the numeric values in element i of the cell array indicate the lags for leading exogenous predictor i.

    Note

    This name-value argument is valid only when you use leading exogenous predictors by specifying the LeadingPredictors name-value argument.

    Example: LeadingPredictorLags=[0 2 4]

    Example: LeadingPredictorLags={0:1,0:2}

    Data Types: single | double | cell

    Predictor lags used for preparing nonleading exogenous predictors, specified as a positive integer vector or a 1-by-q cell array of positive integer vectors, where q is the number of nonleading exogenous predictors.

    • If PredictorLags is a vector, then the software applies each specified lag value in PredictorLags to all the nonleading exogenous predictors. That is, for each element i in the vector, the software shifts the nonleading exogenous predictors backward in time by i steps and uses the resulting feature as a predictor.

    • If PredictorLags is a cell array, then the numeric values in element i of the cell array indicate the lags for nonleading exogenous predictor i.

    Note

    This name-value argument is valid only when you use nonleading exogenous predictors.

    Example: PredictorLags=1:14

    Example: PredictorLags={1:2,1:3,1:2}

    Data Types: single | double | cell

    Response lags used for preparing predictors, specified as a positive integer vector. The software applies each specified lag value in ResponseLags to the response. That is, for each element i in the vector, the software shifts the response backward in time by i steps and uses the resulting feature as a predictor. To create no lagged response variables, specify ResponseLags as [].

    Example: ResponseLags=1:7

    Data Types: single | double

    List of categorical exogenous predictors, specified as one of the values in this table.

    ValueDescription
    Positive integer vector

    Each entry in the vector is an index value indicating that the corresponding exogenous predictor is categorical. The index values are between 1 and p, where p is the number of exogenous predictors listed in PredictorNames.

    Logical vector

    A true entry means that the corresponding exogenous predictor is categorical. The length of the vector is p.

    String array or cell array of character vectorsEach element in the array is the name of a categorical exogenous predictor variable. The names must match the entries in PredictorNames.
    "all"All exogenous predictors are categorical.

    By default, if the exogenous predictors are in a numeric matrix, the software assumes all the exogenous predictors are continuous. If the exogenous predictors are in a table or timetable, the software assumes they are categorical if they are logical vectors, categorical vectors, character arrays, string arrays, or cell arrays of character vectors. However, learners that use decision trees assume that mathematically ordered categorical vectors are continuous variables. To identify any other predictors as categorical predictors, specify them by using the CategoricalPredictors name-value argument.

    The software creates dummy variables based on the Learner name-value argument and the underlying fitting function used to create the regression models in Learners. For more information on how fitting functions treat categorical predictors, see Automatic Creation of Dummy Variables.

    Note

    This name-value argument is valid only when you use exogenous predictors.

    Example: CategoricalPredictors="all"

    Data Types: single | double | logical | string | cell

    Names of the exogenous predictor variables, specified as a string array or cell array of character vectors.

    • If you supply exogenous predictor data using a numeric matrix, then you can use PredictorNames to assign names to the exogenous predictor variables.

      • The order of the names in PredictorNames must correspond to the order of the columns in the matrix.

      • By default, PredictorNames is {'x1','x2',...}.

    • If you supply exogenous predictor data using a table or timetable, then you can use PredictorNames to specify which exogenous variables to use as predictors during training.

      • PredictorNames must be a subset of the variable names in the table or timetable and cannot include the name of the response variable.

      • By default, PredictorNames contains the names of all variables other than the response variable.

    Note

    This name-value argument is valid only when you use exogenous predictors.

    Example: PredictorNames=["Day","Month","Year"]

    Data Types: string | cell

    Name of the response variable Y, specified as a character vector or a string scalar. ResponseName cannot be the name of a variable in X.

    Note

    This name-value argument is valid only when you supply Y as a numeric vector.

    Example: ResponseName="Temperature"

    Data Types: char | string

    Time series data partition for cross-validating the model, specified as a tspartition object. The tspartition object can use one of the following validation schemes: expanding window cross-validation, sliding window cross-validation, or holdout validation.

    If you specify the Partition name-value argument, then directforecaster returns a PartitionedDirectForecaster object. Otherwise, the function returns a DirectForecaster object.

    Example: Partition=tspartition(size(X,1),"ExpandingWindow",5)

    Flag to run computations in parallel, specified as true or false. If you specify UseParallel as true, then the function executes for-loop iterations by using parfor (Parallel Computing Toolbox). The loop runs in parallel when you have Parallel Computing Toolbox™.

    Example: UseParallel=true

    Data Types: logical

    Number of bins for the numeric predictors, specified as a positive integer scalar.

    • If the NumBins value is empty (default), then directforecaster does not bin any predictors.

    • If you specify the NumBins value as a positive integer scalar (numBins), then directforecaster bins every numeric predictor into at most numBins equiprobable bins, and then grows trees on the bin indices instead of the original data.

      • The number of bins can be less than numBins if a predictor has fewer than numBins unique values.

      • directforecaster does not bin categorical predictors.

    When you use a large training data set, this binning option speeds up training but might cause a decrease in accuracy. You can try setting the NumBins value to 50 first, and then change the value depending on the accuracy and training speed.

    Note

    directforecaster supports the NumBins name-value argument for trees and ensembles of trees only. That is, the Learner value must be "tree", "bag", "gam", "lsboost", or a template object created by templateTree, templateGAM, or templateEnsemble.

    Example: NumBins=50

    Data Types: single | double

    Output Arguments

    expand all

    Trained direct forecasting model, returned as a DirectForecaster or PartitionedDirectForecaster model object.

    If you specify the Partition name-value argument, then directforecaster returns a PartitionedDirectForecaster model object. Otherwise, the function returns a DirectForecaster model object.

    Properties

    expand all

    Data Properties

    This property is read-only.

    Indices of categorical exogenous predictors, specified as a positive integer vector. Each index value in CategoricalPredictors indicates that the corresponding exogenous predictor listed in PredictorNames is categorical. If none of the exogenous predictors are categorical, then this property is empty ([]).

    Data Types: double

    This property is read-only.

    Number of observations in the data stored in X and Y, specified as a positive integer scalar.

    Data Types: double

    This property is read-only.

    Names of the exogenous predictors, specified as a cell array of character vectors. The order of the elements in PredictorNames corresponds to the order of the exogenous predictors in the data argument used to train the model.

    Data Types: cell

    This property is read-only.

    Name of the response variable, specified as a character vector.

    Data Types: char

    This property is read-only.

    Exogenous predictor data used to train the model, specified as a numeric matrix, table, or timetable. Each row of X corresponds to one observation, and each column corresponds to one variable.

    This property is read-only.

    Observed response data used to train the model, specified as a numeric vector, one-column table, or one-column timetable. Each row of Y corresponds to one observation.

    Forecasting Properties

    This property is read-only.

    Future time steps at which to forecast, specified as a positive integer vector. Learners contains a trained regression model for each horizon step. For example, if the Horizon value of a direct forecasting model Mdl is [1 3], then Mdl.Learners contains two regression models: one that forecasts at horizon step 1, and one that forecasts at horizon step 3.

    Data Types: double

    This property is read-only.

    Leading predictor lags used for preparing leading exogenous predictors, specified as a nonnegative integer vector or cell array of nonnegative integer vectors.

    • If LeadingPredictorLags is a vector, then for each element i in the vector, the software shifts the leading exogenous predictors backward in time by i steps, relative to the horizon time step. The software uses the resulting features as predictors. When the LeadingPredictorLags value is 0, the software uses the unshifted leading predictors.

      For example, if the Horizon value of a direct forecasting model is 3 and the LeadingPredictorLags value is 0, then the software uses the unshifted leading predictor values at horizon step 3 as predictor values.

    • If LeadingPredictorLags is a cell array, then the numeric values in element i of the cell array indicate the lags for leading exogenous predictor i.

    If no leading predictor lags are used, then this property is empty ([]).

    Data Types: double | cell

    This property is read-only.

    Indices of the leading exogenous predictors, specified as a positive integer vector. Leading predictors are predictors for which future values are known. Each index value in LeadingPredictors indicates that the corresponding exogenous predictor listed in PredictorNames is leading. If no exogenous predictors are leading predictors, then this property is empty ([]).

    Data Types: double

    This property is read-only.

    Compact regression models trained at different horizon steps, specified as a cell array of regression model objects. That is, for a direct forecasting model Mdl, the software trains the regression model Mdl.Learners{1} at horizon step Mdl.Horizon(1).

    This table lists the possible compact regression models.

    Regression Model TypeModel Object
    Bagged or boosted ensemble of treesCompactRegressionEnsemble
    General additive model (GAM)CompactRegressionGAM
    Gaussian process regression (GPR)CompactRegressionGP
    Kernel modelRegressionKernel
    Linear modelRegressionLinear
    Support vector machine (SVM)CompactRegressionSVM
    Decision treeCompactRegressionTree

    Data Types: cell

    This property is read-only.

    Template for the regression models in Learners, specified as the output of one of these template functions.

    Template FunctionDescription
    templateEnsembleEnsemble learning template, with the ensemble aggregation method specified as "Bag" or "LSBoost"
    templateGAMGeneral additive model template
    templateGPGaussian process regression model template
    templateKernelKernel model template
    templateLinearLinear learner template
    templateSVMSupport vector machine template
    templateTreeDecision tree template

    This property is read-only.

    Maximum lag value, specified as a nonnegative integer scalar. The MaxLag value depends on the values in ResponseLags, PredictorLags, and LeadingPredictorLags. Specifically, the software computes the maximum lag as follows:

    MaxLag = max([0,ResponseLags,PredictorLags, ...
    LeadingPredictorLags - min(Horizon) + 1])
    Unlike response lags and nonleading predictor lags, leading predictor lags are relative to horizon time steps instead of the current time step.

    Data Types: double

    This property is read-only.

    Predictor lags used for preparing nonleading exogenous predictors, specified as a positive integer vector or cell array of positive integer vectors.

    • If PredictorLags is a vector, then for each element i in the vector, the software shifts the nonleading exogenous predictors backward in time by i steps and uses the resulting features as predictors.

    • If PredictorLags is a cell array, then the numeric values in element i of the cell array indicate the lags for nonleading exogenous predictor i.

    If no predictor lags are used, then this property is empty ([]).

    Data Types: double | cell

    This property is read-only.

    Response lags used for preparing predictors, specified as a positive integer vector. Each element in ResponseLags indicates the number of time steps by which to shift the response backward in time. The resulting feature is used as a predictor. If no response lags are used, then this property is empty ([]).

    Data Types: double

    Prepared Data Properties

    This property is read-only.

    Indices of the prepared categorical predictors, specified as a positive integer vector. Each index value in PreparedCategoricalPredictors indicates that the corresponding predictor listed in PreparedPredictorNames is categorical. If no prepared predictors are categorical predictors, then this property is empty ([]).

    Data Types: double

    This property is read-only.

    Names of the prepared predictors, specified as a cell array of character vectors. These prepared predictors include variables created from both the exogenous predictor variables and the response variable used to train the direct forecasting model. Not every predictor is used at every horizon step. To see which predictors are used at a specific horizon step, consult the PreparedPredictorsPerHorizon table.

    Data Types: cell

    This property is read-only.

    Prepared predictors at each horizon step, specified as a table of logical values. Each row of the table corresponds to a horizon step, and each column of the table corresponds to a prepared predictor as listed in PreparedPredictorNames.

    For a direct forecasting model Mdl, the logical value in row i and column j indicates whether the software uses prepared predictor Mdl.PreparedPredictorNames(j) at horizon step Mdl.Horizon(i). If the value is 1 (true), then the software uses the predictor. If the value is 0 (false), then the software does not use the predictor.

    Data Types: table

    This property is read-only.

    Names of the prepared responses at each horizon step, specified as a cell array of character vectors. That is, element i of PreparedResponseNames is the name of the response variable at the horizon step specified by element i of Horizon.

    For example, given a direct forecasting model Mdl, the name of the response variable at horizon step Mdl.Horizon(1), Mdl.PreparedResponseNames{1}, matches the response variable name used in the first regression model in Learners (Mdl.Learners{1}.ResponseName).

    Data Types: cell

    Object Functions

    compactReduce size of direct forecasting model
    crossvalCross-validate direct forecasting model
    lossLoss at each horizon step
    predictPredict response at time steps in observed test data
    forecastForecast response at time steps beyond available data
    preparedPredictorsObtain prepared data used for training or testing in direct forecasting

    Examples

    collapse all

    Open Live Script

    Calculate the test set mean squared error (MSE) of a direct forecasting model.

    Load the sample file TemperatureData.csv, which contains average daily temperatures from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.

    temperatures = readtable("TemperatureData.csv");
head(temperatures)
        Year       Month       Day    TemperatureF
    ____    ___________    ___    ____________

    2015    {'January'}     1          23     
    2015    {'January'}     2          31     
    2015    {'January'}     3          25     
    2015    {'January'}     4          39     
    2015    {'January'}     5          29     
    2015    {'January'}     6          12     
    2015    {'January'}     7          10     
    2015    {'January'}     8           4

    For this example, use a subset of the temperature data that omits the first 100 observations.

    Tbl = temperatures(101:end,:);

    Create a datetime variable t that contains the year, month, and day information for each observation in Tbl. Then, use t to convert Tbl into a timetable.

    numericMonth = month(datetime(Tbl.Month, ...
    InputFormat="MMMM",Locale="en_US"));
t = datetime(Tbl.Year,numericMonth,Tbl.Day);
Tbl.Time = t;
Tbl = table2timetable(Tbl);

    Plot the temperature values in Tbl over time.

    plot(Tbl.Time,Tbl.TemperatureF)
xlabel("Date")
ylabel("Temperature in Fahrenheit")

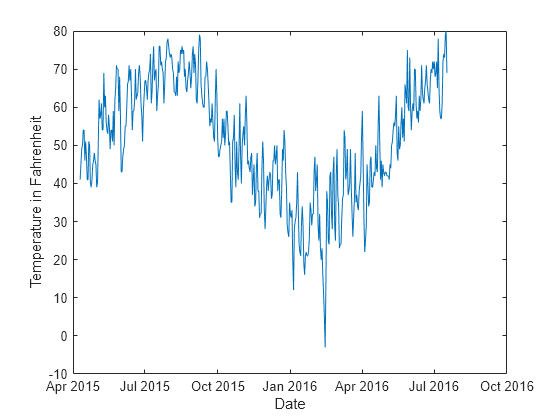
    Figure contains an axes object. The axes object with xlabel Date, ylabel Temperature in Fahrenheit contains an object of type line.

    Partition the temperature data into training and test sets by using tspartition. Reserve 20% of the observations for testing.

    partition = tspartition(size(Tbl,1),"Holdout",0.20);
trainingTbl = Tbl(training(partition),:);
testTbl = Tbl(test(partition),:);

    Create a full direct forecasting model by using the data in trainingTbl. Train the model using a decision tree learner. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known. To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags.

    Mdl = directforecaster(trainingTbl,"TemperatureF", ...
    Learner="tree", ...
    LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ...
    ResponseLags=1:7)
    Mdl = 
  DirectForecaster

                  Horizon: 1
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: 2
                 Learners: {[1x1 classreg.learning.regr.CompactRegressionTree]}
                   MaxLag: 7
          NumObservations: 372

    Mdl is a DirectForecaster model object. By default, the horizon is one step ahead. That is, Mdl predicts a value that is one step into the future.

    Calculate the test set MSE. Smaller MSE values indicate better performance.

    testMSE = loss(Mdl,testTbl)
    testMSE = 
61.0849
    Open Live Script

    After creating a DirectForecaster object, see how the model performs on observed test data by using the predict object function. Then use the model to forecast at time steps beyond the available data by using the forecast object function.

    Load the sample file TemperatureData.csv, which contains average daily temperatures from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.

    temperatures = readtable("TemperatureData.csv");
head(temperatures)
        Year       Month       Day    TemperatureF
    ____    ___________    ___    ____________

    2015    {'January'}     1          23     
    2015    {'January'}     2          31     
    2015    {'January'}     3          25     
    2015    {'January'}     4          39     
    2015    {'January'}     5          29     
    2015    {'January'}     6          12     
    2015    {'January'}     7          10     
    2015    {'January'}     8           4

    For this example, use a subset of the temperature data that omits the first 100 observations.

    Tbl = temperatures(101:end,:);

    Create a datetime variable t that contains the year, month, and day information for each observation in Tbl. Then, use t to convert Tbl into a timetable.

    numericMonth = month(datetime(Tbl.Month, ...
    InputFormat="MMMM",Locale="en_US"));
t = datetime(Tbl.Year,numericMonth,Tbl.Day);
Tbl.Time = t;
Tbl = table2timetable(Tbl);

    Plot the temperature values in Tbl over time.

    plot(Tbl.Time,Tbl.TemperatureF)
xlabel("Date")
ylabel("Temperature in Fahrenheit")

    Figure contains an axes object. The axes object with xlabel Date, ylabel Temperature in Fahrenheit contains an object of type line.

    Partition the temperature data into training and test sets by using tspartition. Reserve 20% of the observations for testing.

    partition = tspartition(size(Tbl,1),"Holdout",0.20);
trainingTbl = Tbl(training(partition),:);
testTbl = Tbl(test(partition),:);

    Create a full direct forecasting model by using the data in trainingTbl. Train the model using a decision tree learner. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known. To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags.

    Mdl = directforecaster(trainingTbl,"TemperatureF", ...
    Learner="tree", ...
    LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ...
    ResponseLags=1:7)
    Mdl = 
  DirectForecaster

                  Horizon: 1
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: 2
                 Learners: {[1x1 classreg.learning.regr.CompactRegressionTree]}
                   MaxLag: 7
          NumObservations: 372

    Mdl is a DirectForecaster model object. By default, the horizon is one step ahead. That is, Mdl predicts a value that is one step into the future.

    For each test set observation, predict the temperature value using Mdl.

    predictedY = predict(Mdl,testTbl)
    predictedY=93×1 timetable
       Time        TemperatureF_Step1
    ___________    __________________

    16-Apr-2016          49.398      
    17-Apr-2016          39.419      
    18-Apr-2016          39.419      
    19-Apr-2016          45.333      
    20-Apr-2016          35.867      
    21-Apr-2016          34.222      
    22-Apr-2016          45.333      
    23-Apr-2016          66.392      
    24-Apr-2016          44.111      
    25-Apr-2016              49      
    26-Apr-2016              49      
    27-Apr-2016          34.222      
    28-Apr-2016          43.333      
    29-Apr-2016          34.222      
    30-Apr-2016          34.222      
    01-May-2016          34.222      
      ⋮

    Plot the true response values and the predicted response values for the test set observations.

    plot(testTbl.Time,testTbl.TemperatureF)
hold on
plot(predictedY.Time,predictedY.TemperatureF_Step1,"--")
hold off
legend("True","Predicted",Location="southeast")
xlabel("Date")
ylabel("Temperature in Fahrenheit")

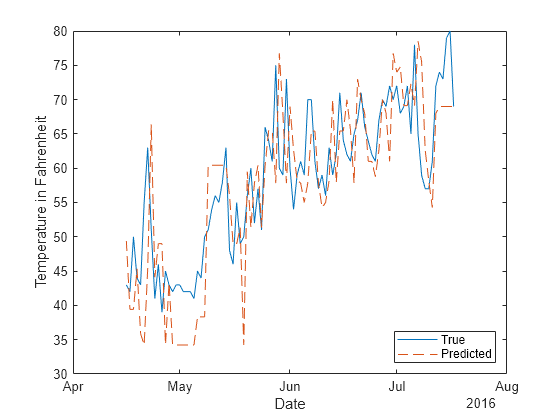
    Figure contains an axes object. The axes object with xlabel Date, ylabel Temperature in Fahrenheit contains 2 objects of type line. These objects represent True, Predicted.

    Overall, the direct forecasting model is able to predict the trend in temperatures.

    Retrain the direct forecasting model using the training and test data. To forecast temperatures one week beyond the available data, specify the horizon steps as one to seven steps ahead.

    finalMdl = directforecaster(Tbl,"TemperatureF", ...
    Learner="tree", ...
    LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ...
    ResponseLags=1:7,Horizon=1:7)
    finalMdl = 
  DirectForecaster

                  Horizon: [1 2 3 4 5 6 7]
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: 2
                 Learners: {7x1 cell}
                   MaxLag: 7
          NumObservations: 465

    finalMdl is a DirectForecaster model object that consists of seven regression models: finalMdl.Learners{1}, which predicts one step into the future; finalMdl.Learners{2}, which predicts two steps into the future; and so on.

    Because finalMdl uses the unshifted values of the leading predictors Year, Month, and Day as predictor values, you must specify these values for the specified horizon steps in the call to forecast. For the week after the last available observation in Tbl, create a timetable forecastData with the year, month, and day values.

    forecastTime = Tbl.Time(end,:)+1:Tbl.Time(end,:)+7;
forecastYear = year(forecastTime);
forecastMonth = month(forecastTime,"name");
forecastDay = day(forecastTime);
forecastData = timetable(forecastTime',forecastYear', ...
    forecastMonth',forecastDay',VariableNames=["Year","Month","Day"])
    forecastData=7×3 timetable
       Time        Year     Month      Day
    ___________    ____    ________    ___

    18-Jul-2016    2016    {'July'}    18 
    19-Jul-2016    2016    {'July'}    19 
    20-Jul-2016    2016    {'July'}    20 
    21-Jul-2016    2016    {'July'}    21 
    22-Jul-2016    2016    {'July'}    22 
    23-Jul-2016    2016    {'July'}    23 
    24-Jul-2016    2016    {'July'}    24

    Forecast the temperature at each horizon step using finalMdl.

    forecastY = forecast(finalMdl,Tbl,LeadingData=forecastData)
    forecastY=7×1 timetable
       Time        TemperatureF
    ___________    ____________

    18-Jul-2016       62.375   
    19-Jul-2016         64.5   
    20-Jul-2016       66.889   
    21-Jul-2016       66.889   
    22-Jul-2016         70.5   
    23-Jul-2016        74.25   
    24-Jul-2016        74.25

    Plot the observed temperatures for the test set data and the forecast temperatures.

    plot(testTbl.Time,testTbl.TemperatureF)
hold on
plot([testTbl.Time(end);forecastY.Time], ...
    [testTbl.TemperatureF(end);forecastY.TemperatureF],"--")
hold off
legend("Observed Data","Forecast Data", ...
    Location="southeast")
xlabel("Date")
ylabel("Temperature in Fahrenheit")

    Figure contains an axes object. The axes object with xlabel Date, ylabel Temperature in Fahrenheit contains 2 objects of type line. These objects represent Observed Data, Forecast Data.

    Open Live Script

    When you perform direct forecasting using directforecaster, the function creates lagged and leading predictors from the training data before fitting a DirectForecaster model. Similarly, the loss and predict object functions reformat the test data before computing loss and prediction values, respectively.

    This example shows how to access the prepared predictor data used by direct forecasting models for training and testing.

    Load the sample file TemperatureData.csv, which contains average daily temperatures from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.

    temperatures = readtable("TemperatureData.csv");
head(temperatures)
        Year       Month       Day    TemperatureF
    ____    ___________    ___    ____________

    2015    {'January'}     1          23     
    2015    {'January'}     2          31     
    2015    {'January'}     3          25     
    2015    {'January'}     4          39     
    2015    {'January'}     5          29     
    2015    {'January'}     6          12     
    2015    {'January'}     7          10     
    2015    {'January'}     8           4

    For this example, use a subset of the temperature data that omits the first 100 observations.

    Tbl = temperatures(101:end,:);

    Create a datetime variable t that contains the year, month, and day information for each observation in Tbl. Then, use t to convert Tbl into a timetable.

    numericMonth = month(datetime(Tbl.Month, ...
    InputFormat="MMMM",Locale="en_US"));
t = datetime(Tbl.Year,numericMonth,Tbl.Day);
Tbl.Time = t;
Tbl = table2timetable(Tbl);

    Plot the temperature values in Tbl over time.

    plot(Tbl.Time,Tbl.TemperatureF)
xlabel("Date")
ylabel("Temperature in Fahrenheit")

    Figure contains an axes object. The axes object with xlabel Date, ylabel Temperature in Fahrenheit contains an object of type line.

    Partition the temperature data into training and test sets by using tspartition. Reserve 20% of the observations for testing.

    partition = tspartition(size(Tbl,1),"Holdout",0.20);
trainingTbl = Tbl(training(partition),:);
testTbl = Tbl(test(partition),:);

    Create a full direct forecasting model by using the data in trainingTbl. Specify the horizon steps as one to seven steps ahead. Train a model at each horizon step using a boosted ensemble of trees. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known.

    To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags. For this example, use the following as predictors values: the current and previous Year values, the current and previous Month values, the current and previous seven Day values, and the previous seven TemperatureF values.

    Mdl = directforecaster(trainingTbl,"TemperatureF", ...
    Horizon=1:7,LeadingPredictors="all", ...
    LeadingPredictorLags={0:1,0:1,0:7}, ...
    ResponseLags=1:7)
    Mdl = 
  DirectForecaster

                  Horizon: [1 2 3 4 5 6 7]
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: 2
                 Learners: {7x1 cell}
                   MaxLag: 7
          NumObservations: 372

    Mdl is a DirectForecaster model object. Mdl consists of seven regression models: Mdl.Learners{1}, which predicts one step into the future; Mdl.Learners{2}, which predicts two steps into the future; and so on.

    Compare the first and seventh regression models in Mdl.

    Mdl.Learners{1}
    ans = 
  CompactRegressionEnsemble
           PredictorNames: {1x19 cell}
             ResponseName: 'TemperatureF_Step1'
    CategoricalPredictors: [10 11]
        ResponseTransform: 'none'
               NumTrained: 100



    Mdl.Learners{7}
    ans = 
  CompactRegressionEnsemble
           PredictorNames: {1x19 cell}
             ResponseName: 'TemperatureF_Step7'
    CategoricalPredictors: [10 11]
        ResponseTransform: 'none'
               NumTrained: 100

    The regression models in Mdl are all CompactRegressionEnsemble objects. Because the models are compact, they do not include the predictor data used to train them.

    To see the data used to train the regression models in Mdl, use the preparedPredictors object function.

    Observe the prepared predictor data used to train Mdl.Learners{1}. By default, preparedPredictors returns the prepared predictor data used at horizon step Mdl.Horizon(1), which in this case is one step ahead.

    prepTrainingTbl1 = preparedPredictors(Mdl,trainingTbl)
    prepTrainingTbl1=372×19 timetable
       Time        TemperatureF_Lag1    TemperatureF_Lag2    TemperatureF_Lag3    TemperatureF_Lag4    TemperatureF_Lag5    TemperatureF_Lag6    TemperatureF_Lag7    Year_Step1    Year_Lag1    Month_Step1    Month_Lag1    Day_Step1    Day_Lag1    Day_Lag2    Day_Lag3    Day_Lag4    Day_Lag5    Day_Lag6    Day_Lag7
    ___________    _________________    _________________    _________________    _________________    _________________    _________________    _________________    __________    _________    ___________    __________    _________    ________    ________    ________    ________    ________    ________    ________

    10-Apr-2015           NaN                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015          NaN        {'April'}     {0x0 char}       10          NaN         NaN         NaN         NaN         NaN         NaN         NaN   
    11-Apr-2015            41                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015         2015        {'April'}     {'April' }       11           10         NaN         NaN         NaN         NaN         NaN         NaN   
    12-Apr-2015            45                   41                  NaN                  NaN                  NaN                  NaN                  NaN              2015         2015        {'April'}     {'April' }       12           11          10         NaN         NaN         NaN         NaN         NaN   
    13-Apr-2015            49                   45                   41                  NaN                  NaN                  NaN                  NaN              2015         2015        {'April'}     {'April' }       13           12          11          10         NaN         NaN         NaN         NaN   
    14-Apr-2015            50                   49                   45                   41                  NaN                  NaN                  NaN              2015         2015        {'April'}     {'April' }       14           13          12          11          10         NaN         NaN         NaN   
    15-Apr-2015            54                   50                   49                   45                   41                  NaN                  NaN              2015         2015        {'April'}     {'April' }       15           14          13          12          11          10         NaN         NaN   
    16-Apr-2015            54                   54                   50                   49                   45                   41                  NaN              2015         2015        {'April'}     {'April' }       16           15          14          13          12          11          10         NaN   
    17-Apr-2015            46                   54                   54                   50                   49                   45                   41              2015         2015        {'April'}     {'April' }       17           16          15          14          13          12          11          10   
    18-Apr-2015            51                   46                   54                   54                   50                   49                   45              2015         2015        {'April'}     {'April' }       18           17          16          15          14          13          12          11   
    19-Apr-2015            47                   51                   46                   54                   54                   50                   49              2015         2015        {'April'}     {'April' }       19           18          17          16          15          14          13          12   
    20-Apr-2015            41                   47                   51                   46                   54                   54                   50              2015         2015        {'April'}     {'April' }       20           19          18          17          16          15          14          13   
    21-Apr-2015            41                   41                   47                   51                   46                   54                   54              2015         2015        {'April'}     {'April' }       21           20          19          18          17          16          15          14   
    22-Apr-2015            51                   41                   41                   47                   51                   46                   54              2015         2015        {'April'}     {'April' }       22           21          20          19          18          17          16          15   
    23-Apr-2015            50                   51                   41                   41                   47                   51                   46              2015         2015        {'April'}     {'April' }       23           22          21          20          19          18          17          16   
    24-Apr-2015            40                   50                   51                   41                   41                   47                   51              2015         2015        {'April'}     {'April' }       24           23          22          21          20          19          18          17   
    25-Apr-2015            39                   40                   50                   51                   41                   41                   47              2015         2015        {'April'}     {'April' }       25           24          23          22          21          20          19          18   
      ⋮

    prepTrainingTbl1 contains lagged predictors (with Lag in their names) and leading predictors (with Step in their names). The table contains missing values due to the creation of these prepared predictors. For example, TemperatureF_Lag1 contains a missing value at time 10-Apr-2015 because the temperature at time 09-Apr-2015 is not known.

    Observe the prepared predictor data used to train Mdl.Learners{7}.

    prepTrainingTbl7 = preparedPredictors(Mdl,trainingTbl, ...
    HorizonStep=7)
    prepTrainingTbl7=372×19 timetable
       Time        TemperatureF_Lag1    TemperatureF_Lag2    TemperatureF_Lag3    TemperatureF_Lag4    TemperatureF_Lag5    TemperatureF_Lag6    TemperatureF_Lag7    Year_Step7    Year_Step6    Month_Step7    Month_Step6    Day_Step7    Day_Step6    Day_Step5    Day_Step4    Day_Step3    Day_Step2    Day_Step1    Day_Lag1
    ___________    _________________    _________________    _________________    _________________    _________________    _________________    _________________    __________    __________    ___________    ___________    _________    _________    _________    _________    _________    _________    _________    ________

    10-Apr-2015           NaN                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015           NaN        {'April'}     {0x0 char}        10           NaN          NaN          NaN          NaN          NaN          NaN         NaN   
    11-Apr-2015           NaN                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        11            10          NaN          NaN          NaN          NaN          NaN         NaN   
    12-Apr-2015           NaN                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        12            11           10          NaN          NaN          NaN          NaN         NaN   
    13-Apr-2015           NaN                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        13            12           11           10          NaN          NaN          NaN         NaN   
    14-Apr-2015           NaN                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        14            13           12           11           10          NaN          NaN         NaN   
    15-Apr-2015           NaN                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        15            14           13           12           11           10          NaN         NaN   
    16-Apr-2015           NaN                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        16            15           14           13           12           11           10         NaN   
    17-Apr-2015            41                  NaN                  NaN                  NaN                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        17            16           15           14           13           12           11          10   
    18-Apr-2015            45                   41                  NaN                  NaN                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        18            17           16           15           14           13           12          11   
    19-Apr-2015            49                   45                   41                  NaN                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        19            18           17           16           15           14           13          12   
    20-Apr-2015            50                   49                   45                   41                  NaN                  NaN                  NaN              2015          2015        {'April'}     {'April' }        20            19           18           17           16           15           14          13   
    21-Apr-2015            54                   50                   49                   45                   41                  NaN                  NaN              2015          2015        {'April'}     {'April' }        21            20           19           18           17           16           15          14   
    22-Apr-2015            54                   54                   50                   49                   45                   41                  NaN              2015          2015        {'April'}     {'April' }        22            21           20           19           18           17           16          15   
    23-Apr-2015            46                   54                   54                   50                   49                   45                   41              2015          2015        {'April'}     {'April' }        23            22           21           20           19           18           17          16   
    24-Apr-2015            51                   46                   54                   54                   50                   49                   45              2015          2015        {'April'}     {'April' }        24            23           22           21           20           19           18          17   
    25-Apr-2015            47                   51                   46                   54                   54                   50                   49              2015          2015        {'April'}     {'April' }        25            24           23           22           21           20           19          18   
      ⋮

    Because Mdl.Learners{7} predicts seven steps ahead, prepTrainingTbl7 contains different predictors from the predictors in prepTrainingTbl1. For example, prepTrainingTbl7 contains the predictors Year_Step7 and Year_Step6 instead of the predictors Year_Step1 and Year_Lag1 in prepTrainingTbl1. The step numbers indicate the horizon steps (that is, the number of time steps ahead).

    Compute the test set mean squared error at each horizon step.

    mse = loss(Mdl,testTbl)
    mse = 1×7

   32.1256   45.3297   49.8831   49.3660   55.7613   50.4300   53.6758

    Obtain the prepared test set predictor data used by Mdl.Learners{1} to compute mse(1). Compare the variables in prepTestTbl1 and prepTrainingTbl1.

    prepTestTbl1 = preparedPredictors(Mdl,testTbl);
isequal(prepTrainingTbl1.Properties.VariableNames, ...
    prepTestTbl1.Properties.VariableNames)
    ans = logical
   1

    The prepared predictors in prepTestTbl1 and prepTrainingTbl1 are the same.

    Similarly, obtain the prepared test set predictor data used by Mdl.Learners{7} to compute mse(7). Compare the variables in prepTestTbl7 and prepTrainingTbl7.

    prepTestTbl7 = preparedPredictors(Mdl,testTbl, ...
    HorizonStep=7);
isequal(prepTrainingTbl7.Properties.VariableNames, ...
    prepTestTbl7.Properties.VariableNames)
    ans = logical
   1

    The prepared predictors in prepTestTbl7 and prepTrainingTbl7 are also the same.

    More About

    expand all

    Extended Capabilities

    Version History

    Introduced in R2023b

    See Also

    | | | | |

    Topics