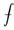int
定积分和不定积分
说明
F = int(___,Name=Value)Name=Value 参量指定附加选项。例如,IgnoreAnalyticConstraints=true 指定 int 对被积函数应用额外的简化。
注意
int 函数以符号形式计算积分,它与 MATLAB® 中的整数数据类型无关。有关整数的详细信息,请参阅整数。
示例
输入参数
名称-值参数
提示
与微分相比,符号积分是一项更为复杂的任务。如果
int无法计算某个表达式的积分,可检查以下原因:原函数不存在封闭形式。
原函数存在,但
int无法找到它。
如果
int无法计算积分的封闭形式,它将返回未求解的积分。对于一些有封闭形式解的积分,如果这些解很复杂且
int返回未求解的积分,您可以使用simplify来获得封闭形式的解。例如,以下代码求f(x)的积分的封闭形式解:syms x f(x) = x*log(x/2+sqrt(x^2+1)); F = int(f,x) simplify(F,Steps=10)除此以外,您可以尝试使用以下方法之一来近似计算未求解的积分:
对于不定积分,使用级数展开。使用此方法在变量的特定值附近对积分进行近似计算。
对于定积分,使用数值近似计算。
对于不定积分,
int不会在结果中返回积分常数。对数学上等价的表达式进行积分时,其结果可能不同。例如,syms x; int((x+1)^2)返回(x+1)^3/3,而syms x; int(x^2+2*x+1)返回(x*(x^2+3*x+3))/3,它与第一个结果相差1/3。对于不定积分,
int隐式假设积分变量var是实数。对于定积分,int将积分变量var限制在指定的积分区间内,除非该区间与现有假设不相符。如果积分界限a和b中的一者或两者不是数值,int会假设a <= b,除非您显式指定其他情况。例如,在默认假设
a <= b下,此代码在(a,b)=(3,2)区间计算定积分时返回结果为 0。syms x a b F(a,b) = int(heaviside(x-1)*heaviside(4-x),a,b); F(3,2)
如果您显式指定假设ans = 0
a > b,则以下代码返回积分结果为 –1。assume(a > b) F(a,b) = int(heaviside(x-1)*heaviside(4-x),a,b); F(3,2)
ans = -1
算法
使用 IgnoreAnalyticConstraints 时,int 会应用以下一些规则:
对于 a 和 b 的所有值,有 log(a) + log(b) = log(a·b) 。特别地,对于 a、b 和 c 的所有值,以下等式成立:
(a·b)c = ac·bc.
对于 a 和 b 的所有值,有 log(ab) = b·log(a) 。特别地,对于 a、b 和 c 的所有值,以下等式成立:
(ab)c = ab·c.
如果 f 和 g 是标准数学函数,并且对于所有小正数都有 f(g(x)) = x,则假设 f(g(x)) = x 对于所有的复数值 x 都成立。特别地:
log(ex) = x
asin(sin(x)) = x, acos(cos(x)) = x, atan(tan(x)) = x
asinh(sinh(x)) = x, acosh(cosh(x)) = x, atanh(tanh(x)) = x
对于朗伯 W 函数的所有分支索引 k,都有 Wk(x·ex) = x。