Main Content

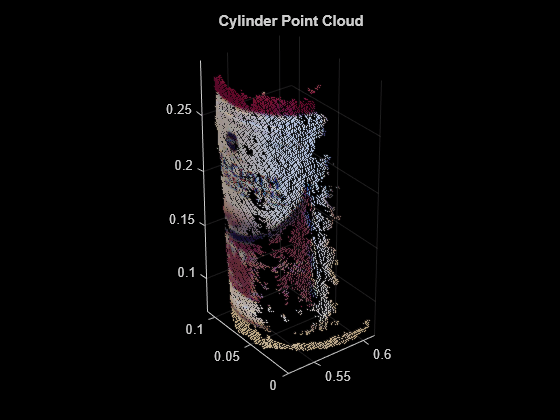
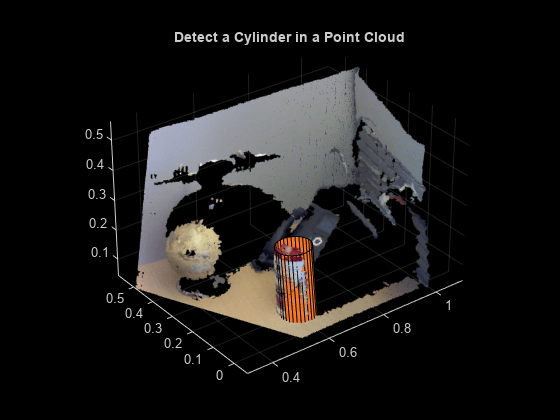
pcfitcylinder

Fit cylinder to 3-D point cloud

collapse all in page

Syntax

model = pcfitcylinder(ptCloudIn,maxDistance)
model = pcfitcylinder(ptCloudIn,maxDistance,referenceVector)
model = pcfitcylinder(ptCloudIn,maxDistance,referenceVector,maxAngularDistance)
[model,inlierIndices,outlierIndices] = pcfitcylinder(___)
[___,meanError] = pcfitcylinder(___)
[___] = pcfitcylinder(___,Name=Value)

Description

model = pcfitcylinder(ptCloudIn,maxDistance) fits a cylinder to a point cloud with a maximum allowable distance from an inlier point to the cylinder. This function uses the M-estimator SAmple Consensus (MSAC) algorithm to find the cylinder.

model = pcfitcylinder(ptCloudIn,maxDistance,referenceVector) fits a cylinder to the point cloud with additional orientation constraints specified by the 1-by-3 reference orientation input vector.

model = pcfitcylinder(ptCloudIn,maxDistance,referenceVector,maxAngularDistance) additionally specifies the maximum allowed absolute angular distance.

[model,inlierIndices,outlierIndices] = pcfitcylinder(___) additionally returns linear indices to the inlier and outlier points in the point cloud input.

[___,meanError] = pcfitcylinder(___) additionally returns the mean error of the distance of the inlier points to the model.

[___] = pcfitcylinder(___,Name=Value) specifies options using one or more name-value arguments in addition to any combination of arguments from previous syntaxes. For example, MaxNumTrials=1000 sets the maximum number of random trials to 1000.

example

Examples

collapse all

Open Live Script

Load the point cloud.

load("object3d.mat");

Display the point cloud.

figure
pcshow(ptCloud)
xlabel("X(m)")
ylabel("Y(m)")
zlabel("Z(m)")
title("Original Point Cloud")

Figure contains an axes object. The axes object with title Original Point Cloud, xlabel X(m), ylabel Y(m) contains an object of type scatter.

Set the maximum point-to-cylinder distance (5 mm) for cylinder fitting.

maxDistance = 0.005;

Set the region of interest to constrain the search.

roi = [0.4 0.6 -Inf 0.2 0.1 Inf];
sampleIndices = findPointsInROI(ptCloud,roi);

Set the orientation constraint.

referenceVector = [0 0 1];

Detect the cylinder and extract it from the point cloud by specifying the inlier points.

[model,inlierIndices] = pcfitcylinder(ptCloud,maxDistance,...
        referenceVector,SampleIndices=sampleIndices);
pc = select(ptCloud,inlierIndices);

Plot the extracted cylinder.

figure
pcshow(pc)
title("Cylinder Point Cloud")

Figure contains an axes object. The axes object with title Cylinder Point Cloud contains an object of type scatter.

Open Live Script

Load a MAT file containing a point cloud into the workspace.

load("object3d.mat");

Display the point cloud.

figure
pcshow(ptCloud)
title("Detect a Cylinder in a Point Cloud")

Set the maximum point-to-cylinder distance for cylinder fitting to 5mm.

maxDistance = 0.005;

Specify a region of interest (ROI) to constrain the fitting function.

roi = [0.4 0.6; -inf 0.2; 0.1 inf];
sampleIndices = findPointsInROI(ptCloud,roi);

Set the orientation constraint for the fitting function

referenceVector = [0 0 1];

Detect the cylinder in the specified ROI of the point cloud and extract it.

model = pcfitcylinder(ptCloud,maxDistance,referenceVector, ...
        SampleIndices=sampleIndices);

Plot the model of the detected cylinder.

hold on
plot(model)

Figure contains an axes object. The axes object with title Detect a Cylinder in a Point Cloud contains 2 objects of type scatter, surface.

Input Arguments

collapse all

Point cloud, specified as a pointCloud object. If the Normal property of the input ptCloud is empty, the function populates it with values to meet the requirements of the fitting algorithm.

Maximum distance from an inlier point to the cylinder, specified as a scalar value. Specify the distance in units that are consistent with the units you are using for the point cloud.

Data Types: single | double

Reference orientation constraint, specified as a 1-by-3 vector.

Maximum absolute angular distance, specified as a scalar value. The maximum angular distance is measured in degrees between the direction of the fitted cylinder and the reference orientation.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'SampleIndices',[].

Linear indices of points to sample in the input point cloud, specified as the comma-separated pair consisting of 'SampleIndices' and a column vector. An empty vector means that all points are candidates to sample when fitting the cylinder during the RANSAC iteration. If you specify a subset of points, the function fits the model by sampling only those points in the subset. Providing a subset of points can significantly speed up the process by reducing the number of trials. You can generate the indices vector using the findPointsInROI method of the pointCloud object.

Maximum number of random trials for finding inliers, specified as the comma-separated pair consisting of 'MaxNumTrials' and a positive integer. To improve robustness of the output, increase this value. However, doing so adds additional computations.

Percentage for finding maximum number of inliers, specified as the comma-separated pair consisting of 'Confidence' and a numeric scalar, in the range (0 100). To improve the robustness of the output, increase this value. However, doing so adds additional computations.

Output Arguments

collapse all

Geometric model of cylinder, returned as a cylinderModel object.

The coefficients for the output model are set to zero when:

  • The input point cloud does not contain enough valid points.

  • The algorithm cannot find enough inlier points.

Linear indices of the inlier points in the input point cloud, returned as a column vector.

Linear indices of the outlier points in the input point cloud returned as a column vector.

Mean error of the distance of inlier points to the model, returned as a scalar value.

Algorithms

The function returns a geometric model that describes the cylinder. This function uses the M-estimator SAmple Consensus (MSAC) algorithm to find the cylinder. The MSAC algorithm is a variant of the RANdom SAmple Consensus (RANSAC) algorithm.

The fitting algorithm for the pcfitcylinder function requires point cloud normals. Therefore, if the Normal property for the input point cloud is empty, the function fills it. When the function fills the Normal property, it uses six points to fit the local cylinder. If six points do not work and the fitting fails, consider calling the pcnormals function which enables you to select the number of points to use.

References

[1] Torr, P. H. S., and A. Zisserman. “MLESAC: A New Robust Estimator with Application to Estimating Image Geometry.” Computer Vision and Image Understanding. Volume 78, Issue 1, April 2000, pp. 138-156.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2015b

See Also

Objects

Functions

Topics