什么是相机标定？

几何相机标定（也称相机后方交会）用于估计图像或视频摄像头镜头与图像传感器的参数。这些参数可用于校正镜头畸变、以世界单位测量目标大小，或确定相机在场景中的位置。此类任务用于机器视觉等应用中，用于检测与测量目标。它们也用于机器人、导航系统和三维场景重新构造。

标定相机后可实现的功能示例：

Examples

相机参数包括内参、外参和畸变系数。要估计相机参数，您需要具备三维世界点及其对应的二维图像点。您可以使用标定模式（如棋盘）的多个图像获得这些对应关系。使用对应关系，您可以求解相机参数。在标定相机后，要评估估计的参数的准确度，您可以：

绘制相机与标定模式的相对位置
计算重投影误差。
计算参数估计误差。

使用相机标定器执行相机标定并评估估计的参数的准确度。

相机模型

Computer Vision Toolbox™ 包含针孔相机模型和鱼眼相机模型的标定算法。鱼眼模型可支持视野 (FOV) 最高达 195 度的相机。

针孔相机标定算法基于让-伊夫·博格特提出的模型 [3]。该模型包含针孔相机模型 [1] 和镜头畸变 [2]。针孔相机模型不考虑镜头畸变，因为理想针孔相机没有镜头。为了准确表示真实相机，算法使用的完整相机模型包含径向和切向镜头畸变。

由于鱼眼镜头产生的极端畸变，针孔模型无法模拟鱼眼相机。有关使用鱼眼模型进行相机标定的详细信息，请参阅Fisheye Calibration Basics。

针孔相机模型

针孔相机是一种没有镜头、只有单个小孔径的简易相机。光线通过孔径在相机另一侧投射出倒立的影像。您可以将虚拟图像平面视为相机前方包含场景正立影像的平面。

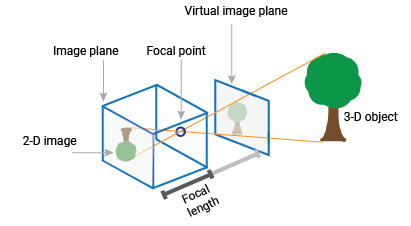
Labeled pinhole camera showing image of tree as 2-D image, image plane, focal point (the pinhole), the virtual plane in front of the camera, and the 3-D object beyond that. Also, the focal length is labeled from the 2-D image in camera to the pinhole and showing that same distance to image plane.

针孔相机参数用一个 3×4 矩阵（称为相机矩阵）表示。此矩阵将三维世界场景映射到图像平面。标定算法使用外参和内参计算相机矩阵。外参表示相机在三维场景中的位置。内参表示相机的光心和焦距。

Matrix operations showing w, (the scale factor) times the column vector x,y,1 (the image points) equal to P times times the column vector x,y,z,1 (the world points). Also, P, (the camera matrix) equal to K, (the intrinsics matrix) times the row vector R, t,(the extrinsics, rotation and translation).

世界点是使用外参变换为相机坐标的。相机坐标则是使用内参映射到图像平面的。

World to camera to image, line of site showing that extrinsic vector [Rt] used for world to camera transformation, and intrinsics K is used for the camera to image transformation.

相机标定参数

标定算法使用外参和内参计算相机矩阵。外参表示从三维世界坐标系到三维相机坐标系的刚性变换。内参表示从三维相机坐标到二维图像坐标的投影变换。

外参

外参包含旋转 R 和平移 t。相机坐标系的原点位于其光心，其 x 和 y 轴定义图像平面。

内参

内参包括焦距、光心（即主点）和偏斜系数。相机内参矩阵 K 定义为：

$[\begin{matrix} f_{x} & s & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{matrix}]$

像素偏斜定义为：

[\begin{matrix} c_{x} & c_{y} \end{matrix}]

- 光心（主点），以像素为单位。

(\begin{matrix} f_{x}, & f_{y} \end{matrix})

- 焦距，以像素为单位。

f_{x} = F / p_{x}

f_{y} = F / p_{y}

F

- 焦距，以世界单位表示，通常以毫米为单位。

(\begin{matrix} p_{x}, & p_{y} \end{matrix})

- 像素大小，以世界单位表示。

s

- 偏斜系数，当图像轴不垂直时该值不为零。

s = f_{x} \tan α

相机标定中的畸变

相机矩阵不考虑镜头畸变，因为理想的针孔相机没有镜头。为了准确表示真实相机，相机模型包含径向和切向镜头畸变。

径向畸变

当光线在镜头旁边比在光心处弯曲更明显时，会发生径向畸变。镜头越小，畸变越大。

Three grids that each represent a type of distortion. One with pincushion distortion (positive radial displacement), one with no distortion, and one with barrel distortion (negative radial displacement)

径向畸变系数用于对此类畸变进行建模。畸变点表示为 (x_distorted, y_distorted)：

x_distorted = x(1 + k₁*r² + k₂*r⁴ + k₃*r⁶)

y_distorted= y(1 + k₁*r² + k₂*r⁴ + k₃*r⁶)

x、y - 未发生畸变的像素位置。x 和 y 采用归一化图像坐标。归一化图像坐标通过平移至光心并除以焦距（以像素为单位）从像素坐标计算得出。因此，x 和 y 为无量纲。
k₁、k₂ 和 k₃ - 镜头的径向畸变系数。
r² = x² + y²

通常，两个系数足以用于标定。对于严重畸变（如广角镜头），可选择包含 k₃ 的三个系数。

切向畸变

当镜头与图像平面不平行时，会发生切向畸变。切向畸变系数用于对此类畸变进行建模。

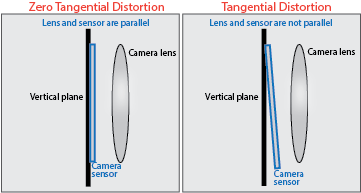
Comparison of zero tangential distortion and tangential distortion

畸变点表示为 (x_distorted, y_distorted)：

x_distorted = x + [2 * p₁ * x * y + p₂ * (r² + 2 * x²)]

y_distorted = y + [p₁ * (r² + 2 *y²) + 2 * p₂ * x * y]

x、y - 未发生畸变的像素位置。x 和 y 采用归一化图像坐标。归一化图像坐标通过平移至光心并除以焦距（以像素为单位）从像素坐标计算得出。因此，x 和 y 为无量纲。
p₁ 和 p₂ - 镜头的切向畸变系数。
r² = x² + y²

参考

[1] Zhang, Z. “A Flexible New Technique for Camera Calibration.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 22, No. 11, 2000, pp. 1330–1334.

[2] Heikkila, J., and O. Silven. “A Four-step Camera Calibration Procedure with Implicit Image Correction.” IEEE International Conference on Computer Vision and Pattern Recognition.1997.

[3] Bouguet, J. Y. “Camera Calibration Toolbox for Matlab.” Computational Vision at the California Institute of Technology.

[4] Bradski, G., and A. Kaehler. Learning OpenCV: Computer Vision with the OpenCV Library. Sebastopol, CA: O'Reilly, 2008.

另请参阅

App

相机标定器 | 立体相机标定器