Constant-Q, Data-Adaptive, and Quadratic Time-Frequency Transforms
Obtain the constant-Q transform (CQT) of a signal, and invert the transform for perfect reconstruction. Decompose a signal using an adaptive wavelet subdivision scheme. Perform data-adaptive time-frequency analysis of nonlinear and nonstationary processes. Decompose a nonlinear or nonstationary process into its intrinsic modes of oscillation. Perform time-frequency filtering using the discrete Gabor transform (DGT) and Gabor multipliers. Obtain instantaneous frequency estimates of a multicomponent nonlinear or nonstationary signal. Return the Wigner-Ville and cross Wigner-Ville distributions of signals.
Functions
cqt | Constant-Q nonstationary Gabor transform |
icqt | Inverse constant-Q transform using nonstationary Gabor frames |
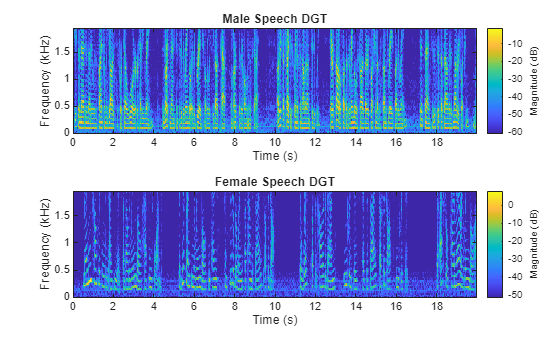
dgt | Discrete Gabor transform (Since R2025a) |
tffilt | Time-frequency filtering using binary mask and Gabor transform (Since R2025a) |
emd | Empirical mode decomposition |
ewt | Empirical wavelet transform |
hht | Hilbert-Huang transform |
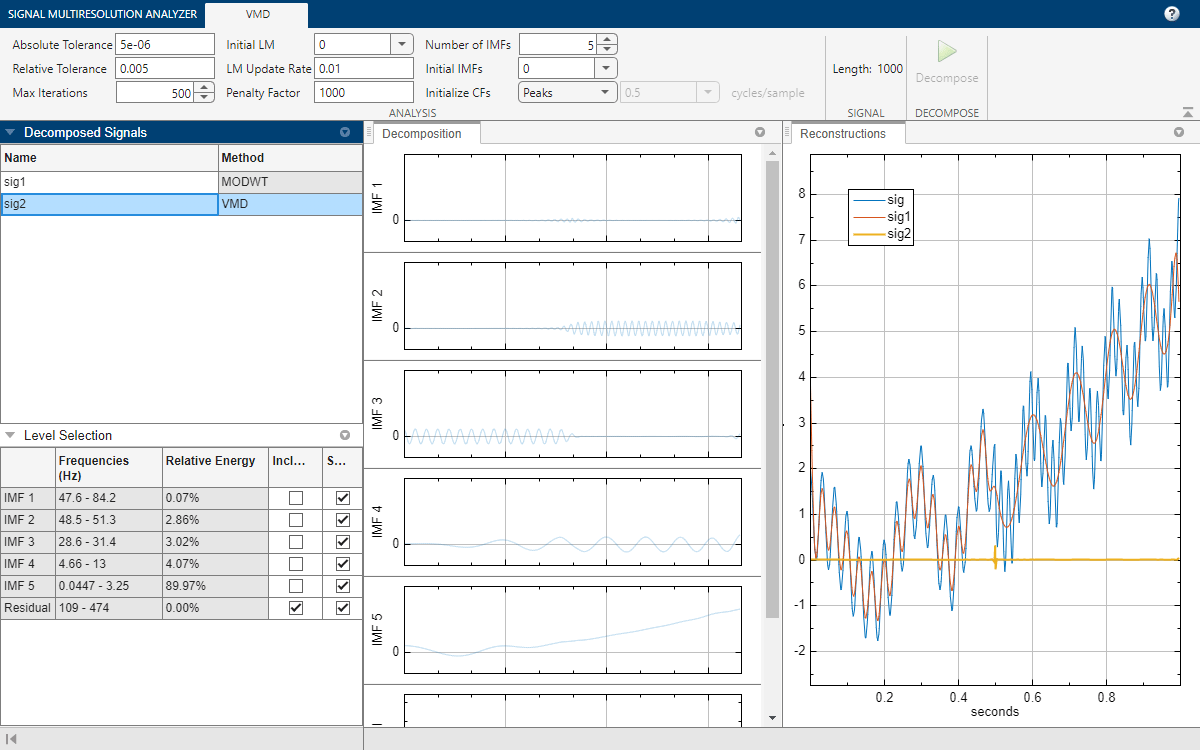
vmd | Variational mode decomposition |
wvd | Wigner-Ville distribution and smoothed pseudo Wigner-Ville distribution |
xwvd | Cross Wigner-Ville distribution and cross smoothed pseudo Wigner-Ville distribution |
Apps
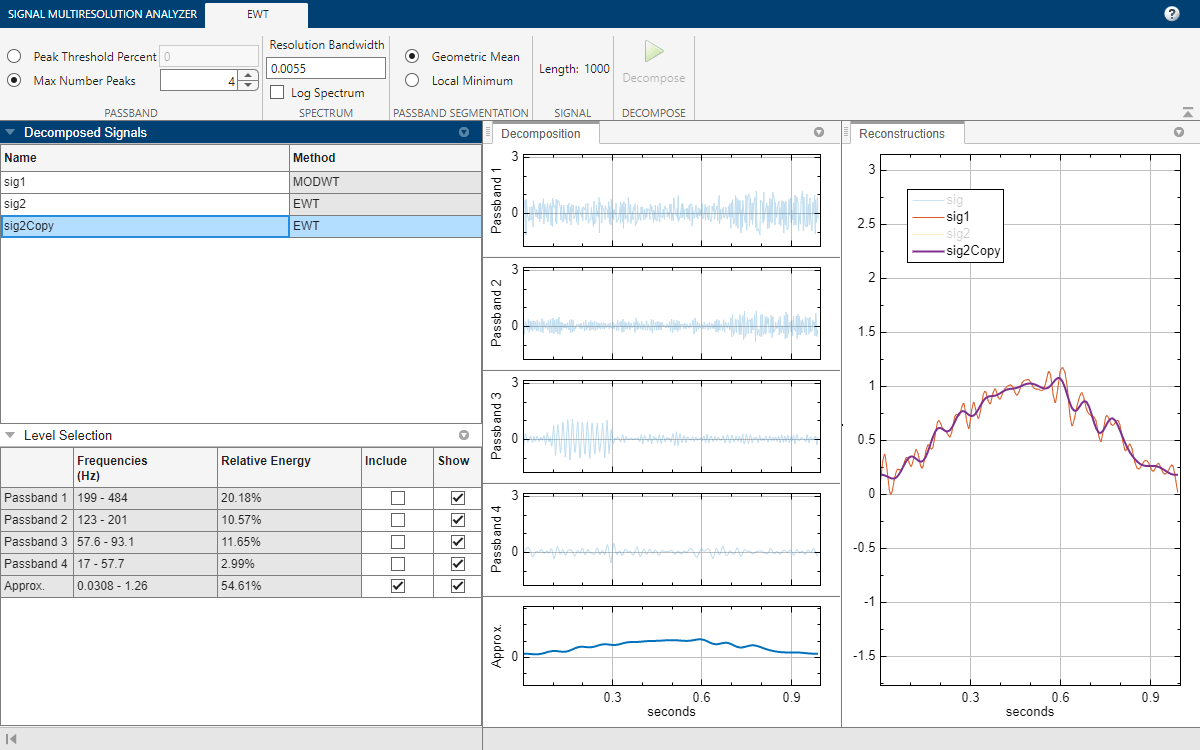
| Signal Multiresolution Analyzer | Decompose signals into time-aligned components |
Topics
- Nonstationary Gabor Frames and the Constant-Q Transform
Learn about frequency-adaptive analysis of signals.
- Empirical Wavelet Transform
Learn about the empirical wavelet transform.