pade
具有时滞的模型的帕德逼近
说明
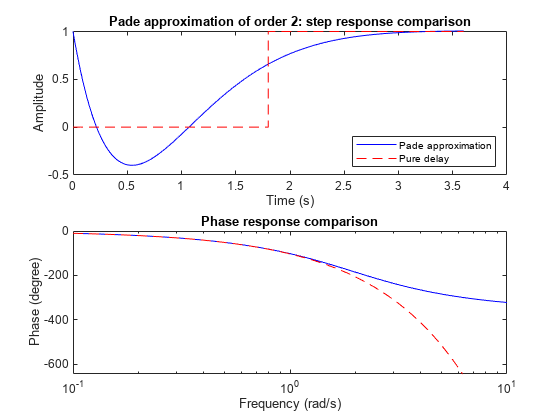
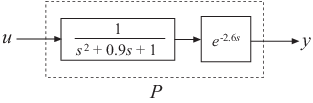
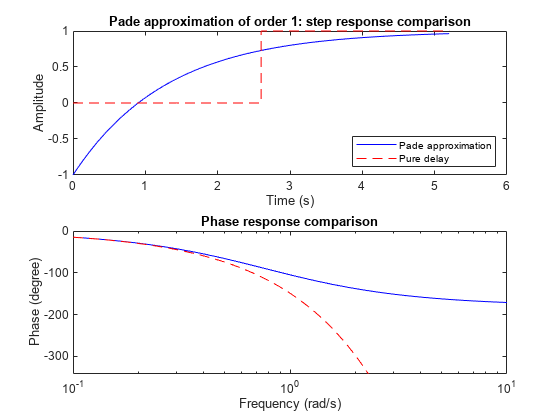
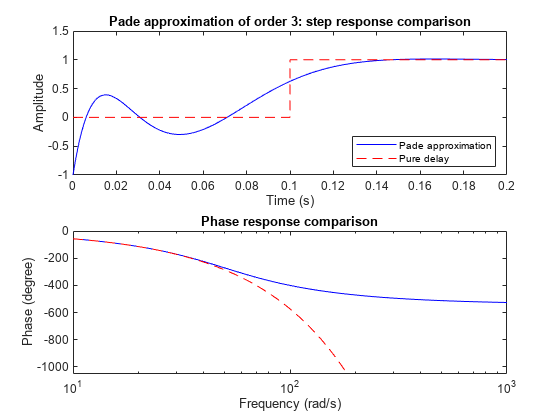
pade 能逼近连续时间 LTI 模型的时滞。此类逼近可用于在连续时间系统上下文中对传输延迟、计算延迟等时滞效应进行建模。时滞为 T 秒的拉普拉斯变换为 exp(–sT)。该指数传递函数使用 [1] 中的帕德逼近公式被逼近为有理传递函数。
如需逼近离散时间模型，请使用 absorbDelay。
有关具有时滞的模型的详细信息，请参阅线性系统中的时滞。
示例
对于此示例，计算时滞为 1.8 秒的二阶系统的无延迟分子和分母系数。
T = 1.8; N = 2; [num,den] = pade(T,N)
num = 1×3
1.0000 -3.3333 3.7037
den = 1×3
1.0000 3.3333 3.7037
绘制无延迟逼近与具有时滞的原始系统的阶跃响应和相位响应。使用 pade 命令而不指定输出参量来生成比较图。
pade(T,N)
对于此示例，求出如下连续时间开环系统的帕德逼近。
创建含输出延迟的开环系统。
s = tf('s');
T = 2.6;
sys = exp(-T*s)/(s^2+0.9*s+1)sys =
1
exp(-2.6*s) * ---------------
s^2 + 0.9 s + 1
Continuous-time transfer function.
Model Properties
sys 是具有时滞的二阶传递函数 (tf) 对象。
接下来，计算 sys 的一阶帕德逼近。
sysx = pade(sys,1)
sysx =
-s + 0.7692
----------------------------------
s^3 + 1.669 s^2 + 1.692 s + 0.7692
Continuous-time transfer function.
Model Properties
pade 会将 sys 中所有时滞替换为一阶逼近。因此，sysx 是无延迟的三阶传递函数。
您还可以绘制并比较无延迟逼近模型与具有时滞的模型的阶跃响应和相位响应。使用时滞和阶数值创建绘图。
pade(T,1)
计算 0.1 秒 I/O 延迟的三阶帕德逼近。
s = tf('s');
sys = exp(-0.1*s);
sysx = pade(sys,3)sysx = -s^3 + 120 s^2 - 6000 s + 1.2e05 -------------------------------- s^3 + 120 s^2 + 6000 s + 1.2e05 Continuous-time transfer function. Model Properties
这里，sys 是 0.1 秒精确时滞的动态系统表示。sysx 是逼近该时滞的传递函数。
比较真实时滞与其逼近的时间响应和频率响应。调用 pade 命令而不指定输出参量来生成比较图。在这种情况下，pade 的第一个参量只是精确时滞的幅值，而非表示时滞的动态系统。
pade(0.1,3)
对于此示例，假设 ssModel.mat 中包含 MIMO 状态空间模型 sys。sys 具有两个输入和三个输出，并且包含输入、输出和内部延迟。
加载数据并检查 sys。
load('ssModel.mat','sys') sys
sys =
A =
x1 x2
x1 2.893 1.497
x2 -0.1138 -0.5279
B =
u1 u2
x1 -1.334 -4.155
x2 1.127 -0.06161
C =
x1 x2
y1 -2.416 -0.6317
y2 1.688 1.063
y3 3.509 1.84
D =
u1 u2
y1 1.019 1.999
y2 0 -3.658
y3 0 -5.885
(values computed with all internal delays set to zero)
Input delays (seconds): 1.5 0.3
Output delays (seconds): 0.2 0.8 1.3
Internal delays (seconds): 2.1 1.3
Continuous-time state-space model.
Model Properties
指定输入、输出和内部延迟的逼近阶数，并计算帕德逼近。将逼近阶数设置为 Inf，以避免逼近相应的延迟。
NU = [3 Inf]; NY = [1 Inf 2]; NINT = [Inf 2]; sysx = pade(sys,NU,NY,NINT)
sysx =
A =
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
x1 -10 0 0 -9.665 -2.527 -7.305 0 16.3 0 4.527
x2 0 -4.615 -3.55 14.04 7.358 21.51 0 0 0 0
x3 0 2 0 0 0 0 0 0 0 0
x4 0 0 0 2.893 1.497 4.115 0 -5.335 0 -1.482
x5 0 0 0 -0.1138 -0.5279 -0.2169 0 4.51 0 1.253
x6 0 0 0 -8.011 -3.193 -4.615 -3.55 0 0 0
x7 0 0 0 0 0 2 0 0 0 0
x8 0 0 0 0 0 0 0 -8 -6.667 -2.222
x9 0 0 0 0 0 0 0 4 0 0
x10 0 0 0 0 0 0 0 0 4 0
B =
u1 u2
x1 -4.075 7.996
x2 0 -23.54
x3 0 0
x4 1.334 -4.155
x5 -1.127 -0.06161
x6 0 10.1
x7 0 0
x8 4 0
x9 0 0
x10 0 0
C =
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
y1 5 0 0 2.416 0.6317 1.826 0 -4.075 0 -1.132
y2 0 0 0 1.688 1.063 3.074 0 0 0 0
y3 0 -2.308 0 3.509 1.84 5.377 0 0 0 0
D =
u1 u2
y1 1.019 -1.999
y2 0 -3.658
y3 0 -5.885
(values computed with all internal delays set to zero)
Input delays (seconds): 0 0.3
Output delays (seconds): 0 0.8 0
Internal delays (seconds): 2.1
Continuous-time state-space model.
Model Properties
在相应逼近阶数设置为 Inf 的位置，所得逼近 sysx 仍具有特定的输入、输出和内部延迟。
输入参数
输出参量
限制
帕德逼近仅在低频段有效，且频域逼近效果优于时域逼近效果。因此，需要比较真实响应与逼近响应，以选择合适的逼近阶数并验证逼近有效性。
高阶帕德逼近会生成极点聚类的传递函数。由于此类极点配置对扰动极为敏感，因此应避免使用阶数为
N>10的帕德逼近。
参考
[1] Golub, Gene H., and Charles F. Van Loan. Matrix Computations. 2nd ed. Johns Hopkins Series in the Mathematical Sciences 3. Baltimore, Md: Johns Hopkins University Press, 1989. pp. 557-558.
版本历史记录
在 R2006a 之前推出
