Main Content

TuningGoal.MinLoopGain

Minimum loop gain constraint for control system tuning

expand all in page

Description

Use the TuningGoal.MinLoopGain object to enforce a minimum loop gain in a particular frequency band. Use this tuning goal with control system tuning commands such as systune or looptune.

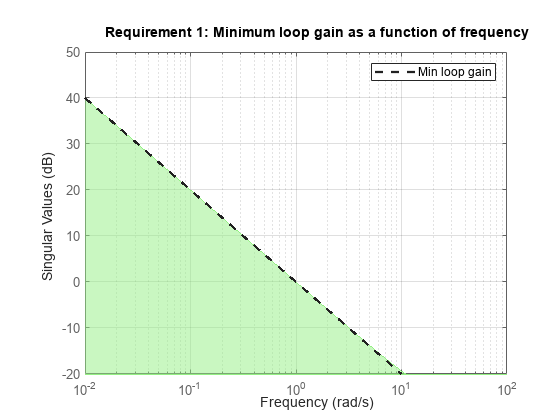
This tuning goal imposes a minimum gain on the open-loop frequency response (L) at a specified location in your control system. You specify the minimum open-loop gain as a function of frequency (a minimum gain profile). For MIMO feedback loops, the specified gain profile is interpreted as a lower bound on the smallest singular value of L.

When you tune a control system, the minimum gain profile is converted to a minimum gain constraint on the inverse of the sensitivity function, inv(S)  = (I + L).

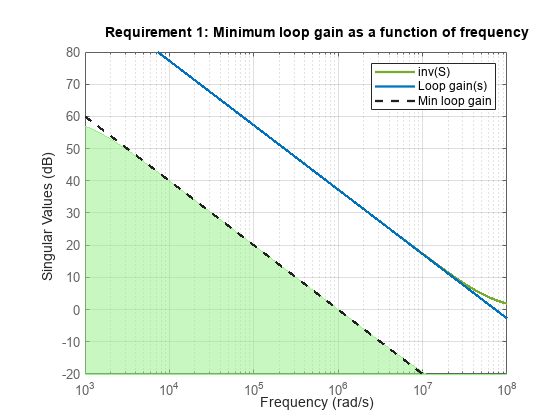
The following figure shows a typical specified minimum gain profile (dashed line) and a resulting tuned loop gain, L (blue line). The shaded region represents gain profile values that are forbidden by this tuning goal. The figure shows that when L is much larger than 1, imposing a minimum gain on inv(S) is a good proxy for a minimum open-loop gain.

TuningGoal.MinLoopGain and TuningGoal.MaxLoopGain specify only low-gain or high-gain constraints in certain frequency bands. When you use these tuning goals, systune and looptune determine the best loop shape near crossover. When the loop shape near crossover is simple or well understood (such as integral action), you can use TuningGoal.LoopShape to specify that target loop shape.

Creation

Syntax

Req = TuningGoal.MinLoopGain(location,loopgain)
Req = TuningGoal.MinLoopGain(location,fmin,gmin)

Description

Req = TuningGoal.MinLoopGain(location,loopgain) creates a tuning goal for boosting the gain of a SISO or MIMO feedback loop. The tuning goal specifies that the open-loop frequency response (L) measured at the specified locations exceeds the minimum gain profile specified by loopgain.

You can specify the minimum gain profile as a smooth transfer function or sketch a piecewise error profile using an frd model or the makeweight (Robust Control Toolbox) command. Only gain values greater than 1 are enforced.

For MIMO feedback loops, the specified gain profile is interpreted as a lower bound on the smallest singular value of L.

example

Req = TuningGoal.MinLoopGain(location,fmin,gmin) specifies a minimum gain profile of the form loopgain = K/s (integral action). The software chooses K such that the gain value is gmin at the specified frequency, fmin.

Input Arguments

expand all

Location at which the maximum open-loop gain is constrained, specified as a character vector or cell array of character vectors that identify one or more locations in the control system to tune. What loop-opening locations are available depends on what kind of system you are tuning:

  • If you are tuning a Simulink® model of a control system, you can use any linear analysis point marked in the model, or any linear analysis point in an slTuner (Simulink Control Design) interface associated with the Simulink model. Use addPoint (Simulink Control Design) to add analysis points to the slTuner interface. For example, if the slTuner interface contains an analysis point u, you can use 'u' to refer to that point when creating tuning goals. Use getPoints (Simulink Control Design) to get the list of analysis points available in an slTuner interface to your model.

  • If you are tuning a generalized state-space (genss) model of a control system, you can use any AnalysisPoint location in the control system model. For example, the following code creates a PI loop with an analysis point at the plant input 'u'. 

    AP = AnalysisPoint('u');
G = tf(1,[1 2]);
C = tunablePID('C','pi');
T = feedback(G*AP*C,1);

    When creating tuning goals, you can use 'u' to refer to the analysis point at the plant input. Use getPoints to get the list of analysis points available in a genss model.

If location is a cell array of loop-opening locations, then the minimum gain goal applies to the resulting MIMO loop.

Minimum open-loop gain as a function of frequency.

You can specify loopgain as a smooth SISO transfer function (tf, zpk, or ss model). Alternatively, you can sketch a piecewise gain profile using a frd model or the makeweight (Robust Control Toolbox) command. For example, the following frd model specifies a minimum gain of 100 (40 dB) below 0.1 rad/s, rolling off at a rate of –20 dB/dec at higher frequencies.

loopgain = frd([100 100 10],[0 1e-1 1]);

When you use an frd model to specify loopgain, the software automatically maps your specified gain profile to a zpk model. The magnitude of this model approximates the desired gain profile. Use viewGoal(Req) to plot the magnitude of that zpk model.

Only gain values larger than 1 are enforced. For multi-input, multi-output (MIMO) feedback loops, the gain profile is interpreted as a lower bound on the smallest singular value of L. For more information about singular values, see sigma.

If you are tuning in discrete time (that is, using a genss model or slTuner interface with nonzero Ts), you can specify loopgain as a discrete-time model with the same Ts. If you specify loopgain in continuous time, the tuning software discretizes it. Specifying the loop gain in discrete time gives you more control over the loop gain near the Nyquist frequency.

Frequency of minimum gain gmin, specified as a scalar value in rad/s.

Use this argument to specify a minimum gain profile of the form loopgain = K/s (integral action). The software chooses K such that the gain value is gmin at the specified frequency, fmin.

Value of minimum gain occurring at fmin, specified as a scalar absolute value.

Use this argument to specify a minimum gain profile of the form loopgain = K/s (integral action). The software chooses K such that the gain value is gmin at the specified frequency, fmin.

Properties

expand all

Minimum open-loop gain as a function of frequency, specified as a SISO zpk model.

The software automatically maps the input argument loopgain onto a zpk model. The magnitude of this zpk model approximates the desired gain profile. Alternatively, if you use the fmin and gmin arguments to specify the gain profile, this property is set to K/s. The software chooses K such that the gain value is gmin at the specified frequency, fmin.

Use viewGoal(Req) to plot the magnitude of the open-loop minimum gain profile.

Frequency band in which tuning goal is enforced, specified as a row vector of the form [min,max]. For continuous time, the default value is equal to [0,Inf]. For discrete time, the default value is equal to [0,pi/Ts], where Ts is the model sample time.

Set the Focus property to limit enforcement of the tuning goal to a particular frequency band. Express this value in the frequency units of the control system model you are tuning (rad/TimeUnit). For example, suppose Req is a tuning goal that you want to apply only between 1 and 100 rad/s. To restrict the tuning goal to this band, use the following command:

Req.Focus = [1,100];

Stability requirement on closed-loop dynamics, specified as 1 (true) or 0 (false).

When Stabilize is true, this requirement stabilizes the specified feedback loop, as well as imposing gain or loop-shape requirements. Set Stabilize to false if stability for the specified loop is not required or cannot be achieved.

Toggle for automatically scaling loop signals, specified as 'on' or 'off'.

In multi-loop or MIMO control systems, the feedback channels are automatically rescaled to equalize the off-diagonal terms in the open-loop transfer function (loop interaction terms). Set LoopScaling to 'off' to disable such scaling and shape the unscaled open-loop response.

Location at which minimum loop gain is constrained, specified as a cell array of character vectors that identify one or more analysis points in the control system to tune. For example, if Location = {'u'}, the tuning goal evaluates the open-loop response measured at an analysis point 'u'. If Location = {'u1','u2'}, the tuning goal evaluates the MIMO open-loop response measured at analysis points 'u1' and 'u2'.

The value of the Location property is set by the location input argument when you create the tuning goal.

Models to which the tuning goal applies, specified as a vector of indices.

Use the Models property when tuning an array of control system models with systune, to enforce a tuning goal for a subset of models in the array. For example, suppose you want to apply the tuning goal, Req, to the second, third, and fourth models in a model array passed to systune. To restrict enforcement of the tuning goal, use the following command:

Req.Models = 2:4;

When Models = NaN, the tuning goal applies to all models.

Feedback loops to open when evaluating the tuning goal, specified as a cell array of character vectors that identify loop-opening locations. The tuning goal is evaluated against the open-loop configuration created by opening feedback loops at the locations you identify.

If you are using the tuning goal to tune a Simulink model of a control system, then Openings can include any linear analysis point marked in the model, or any linear analysis point in an slTuner (Simulink Control Design) interface associated with the Simulink model. Use addPoint (Simulink Control Design) to add analysis points and loop openings to the slTuner interface. Use getPoints (Simulink Control Design) to get the list of analysis points available in an slTuner interface to your model.

If you are using the tuning goal to tune a generalized state-space (genss) model of a control system, then Openings can include any AnalysisPoint location in the control system model. Use getPoints to get the list of analysis points available in the genss model.

For example, if Openings = {'u1','u2'}, then the tuning goal is evaluated with loops open at analysis points u1 and u2.

Name of the tuning goal, specified as a character vector.

For example, if Req is a tuning goal:

Req.Name = 'LoopReq';

Examples

collapse all

Open Live Script

Create a tuning goal that boosts the open-loop gain of a feedback loop to at least a specified profile.

Suppose that you are tuning a control system that has a loop-opening location identified by PILoop. Specify that the open-loop gain measured at that location exceeds a minimum gain of 10 (20 dB) below 0.1 rad/s, rolling off at a rate of -20 dB/dec at higher frequencies. Use an frd model to sketch this gain profile.

loopgain = frd([10 10 0.1],[0 1e-1 10]);
Req = TuningGoal.MinLoopGain('PILoop',loopgain);

The software converts loopgain into a smooth function of frequency that approximates the piecewise-specified gain profile. Display the tuning goal using viewGoal.

viewGoal(Req)

MATLAB figure

The dashed line shows the specified the gain profile. The shaded region indicates where the tuning goal is violated, except that gain values less than 1 are not enforced. Therefore, this tuning goal only specifies a minimum gain at frequencies below 1 rad/s.

You can use Req as an input to looptune or systune when tuning the control system. Then use viewGoal(Req,T) to compare the tuned loop gain to the minimum gain specified in the tuning goal, where T represents the tuned control system.

Open Live Script

Create a tuning goal that specifies a minimum loop gain profile of the form L = K / s. The gain profile attains the value of -20 dB (0.01) at 100 rad/s.

Req = TuningGoal.MinLoopGain('X',100,0.01);
viewGoal(Req)

MATLAB figure

viewGoal confirms that the tuning goal is correctly specified. You can use this tuning goal to tune a control system that has a loop-opening location identified as 'X'. Since loop gain values less than 1 are ignored, this tuning goal specifies minimum gain only below 1 rad/s, with no restriction on loop gain at higher frequency.

Although the specified gain profile (dashed line) is a pure integrator, for numeric reasons, the gain profile enforced during tuning levels off at very low frequencies, as described in Algorithms. To see the regularized gain profile, expand the axes of the tuning-goal plot.

xlim([10^-4,10^2])
ylim([-20,80])

MATLAB figure

The shaded region reflects the modified gain profile.

Open Live Script

Examine a minimum loop gain tuning goal against the tuned loop gain. A minimum loop gain tuning goal is converted to a constraint on the gain of the sensitivity function at the location specified in the tuning goal.

To see this relationship between the minimum loop gain and the sensitivity function, tune the following closed-loop system with analysis points at X1 and X2. The control system has tunable PID controllers C1 and C2.

Create a model of the control system.

G2 = zpk([],-2,3);
G1 = zpk([],[-1 -1 -1],10);
C20 = tunablePID('C2','pi');
C10 = tunablePID('C1','pid');
X1 = AnalysisPoint('X1');
X2 = AnalysisPoint('X2');
InnerLoop = feedback(X2*G2*C20,1);
CL0 = feedback(G1*InnerLoop*C10,X1);
CL0.InputName = 'r';
CL0.OutputName = 'y';

Specify some tuning goals, including a minimum loop gain. Tune the control system to these requirements.

Rtrack = TuningGoal.Tracking('r','y',10,0.01);
Rreject = TuningGoal.Gain('X2','y',0.1);
Rgain = TuningGoal.MinLoopGain('X2',100,10000);
Rgain.Openings = 'X1';

opts = systuneOptions('RandomStart',2);
rng('default');  % for reproducibility
[CL,fSoft] = systune(CL0,[Rtrack,Rreject,Rgain]);
Final: Soft = 1.07, Hard = -Inf, Iterations = 109
       Some closed-loop poles are marginally stable (decay rate near 1e-07)

Examine the TuningGoal.MinLoopGain goal against the corresponding tuned response. 

viewGoal(Rgain,CL)

MATLAB figure

The plot shows the achieved loop gain for the loop at X2 (blue line). The plot also shows the inverse of the achieved sensitivity function, S, at the location X2 (green line). The inverse sensitivity function at this location is given by inv(S) = I+L. Here, L is the open-loop point-to-point loop transfer measured at X2.

The minimum loop gain goal Rgain is constraint on inv(S), represented in the plot by the green shaded region. The constraint on inv(S) can be thought of as a minimum gain constraint on L that applies where the gain of L (or the smallest singular value of L, for MIMO loops) is greater than 1.

Open Live Script

Create requirements that specify a minimum loop gain of 20 dB (100) at 50 rad/s and a maximum loop gain of -20 dB (0.01) at 1000 rad/s on the inner loop of the following control system.

Create the maximum and minimum loop gain requirements.

RMinGain = TuningGoal.MinLoopGain('X2',50,100);
RMaxGain = TuningGoal.MaxLoopGain('X2',1000,0.01);

Configure the requirements to apply to the loop gain of the inner loop measured with the outer loop open.

RMinGain.Openings = 'X1';
RMaxGain.Openings = 'X1';

Setting Req.Openings tells the tuning algorithm to enforce the requirements with a loop open at the specified location. With the outer loop open, the requirements apply only to the inner loop.

By default, tuning using TuningGoal.MinLoopGain or TuningGoal.MaxLoopGain imposes a stability requirement as well as the minimum or maximum loop gain. Practically, in some control systems it is not possible to achieve a stable inner loop. In that case, remove the stability requirement for the inner loop by setting the Stabilize property to false.

RMinGain.Stabilize = false;
RMaxGain.Stabilize = false;

When you tune using either of these requirements, the tuning algorithm still imposes a stability requirement on the overall tuned control system, but not on the inner loop alone.

Tips

  • This tuning goal imposes an implicit stability constraint on the closed-loop sensitivity function measured at Location, evaluated with loops opened at the points identified in Openings. The dynamics affected by this implicit constraint are the stabilized dynamics for this tuning goal. The MinDecay and MaxRadius options of systuneOptions control the bounds on these implicitly constrained dynamics. If the optimization fails to meet the default bounds, or if the default bounds conflict with other requirements, use systuneOptions to change these defaults.

Algorithms

When you tune a control system using a TuningGoal, the software converts the tuning goal into a normalized scalar value f(x). Here, x is the vector of free (tunable) parameters in the control system. The software then adjusts the parameter values to minimize f(x) or to drive f(x) below 1 if the tuning goal is a hard constraint.

For TuningGoal.MinLoopGain, f(x) is given by:

f(x)=‖WS(D−1SD)‖∞.

Here, D is a diagonal scaling (for MIMO loops). S is the sensitivity function at Location. WS is a frequency-weighting function derived from the minimum loop gain profile, MinGain. The gain of this function roughly matches MaxGain for values ranging from –20 dB to 60 dB. For numerical reasons, the weighting function levels off outside this range, unless the specified gain profile changes slope outside this range. This adjustment is called regularization. Because poles of WS close to s = 0 or s = Inf might lead to poor numeric conditioning of the systune optimization problem, it is not recommended to specify gain profiles with very low-frequency or very high-frequency dynamics.

To obtain WS, use:

WS = getWeight(Req,Ts)

where Req is the tuning goal, and Ts is the sample time at which you are tuning (Ts = 0 for continuous time). For more information about regularization and its effects, see Visualize Tuning Goals.

Although S is a closed-loop transfer function, driving f(x) < 1 is equivalent to enforcing a lower bound on the open-loop transfer function, L, in a frequency band where the gain of L is greater than 1. To see why, note that S = 1/(1 + L). For SISO loops, when |L| >> 1, |S | ≈ 1/|L|. Therefore, enforcing the open-loop minimum gain requirement, |L| > |WS|, is roughly equivalent to enforcing |WsS| < 1. For MIMO loops, similar reasoning applies, with ||S|| ≈ 1/σmin(L), where σmin is the smallest singular value.

For an example illustrating the constraint on S, see Minimum Loop Gain as Constraint on Sensitivity Function.

Version History

Introduced in R2016a

expand all

See Also

| | (Simulink Control Design) | (Simulink Control Design) | | | | | | | (Simulink Control Design) |

Topics