使用浅层神经网络拟合数据
神经网络擅长拟合函数。事实上有证据表明,一个简单的神经网络就可以拟合任何实用函数。
例如,假设您有一家健康诊所的数据。您想要设计一个网络,该网络可以基于 13 个解剖学测量值来预测人的体脂率。您总共有 252 个人的样本,其中包括这 13 项数据和相关的体脂率。
您可以用两种方法解决此问题:
使用神经网络拟合,如使用神经网络拟合对数据进行拟合中所述。
使用命令行函数,如使用命令行函数拟合数据中所述。
一般最好从 App 开始,然后使用该 App 自动生成命令行脚本。在使用任何方法之前,首先通过选择数据集来定义问题。每个神经网络 App 都可以访问许多采样数据集,您可以使用这些数据集来试验工具箱(请参阅浅层神经网络的样本数据集)。如果您有要解决的特定问题,可以将您自己的数据加载到工作区中。下一节介绍数据格式。
提示
要以交互方式构建和可视化深度学习神经网络,请使用深度网络设计器。有关详细信息,请参阅深度网络设计器快速入门。
定义问题
要为工具箱定义拟合(回归)问题,请将一组输入向量(预测变量)排列为矩阵中的列。然后,将一组响应(每个输入向量的正确输出向量)排列成第二个矩阵。例如,您可以定义一个具有四个观测值的回归问题,每个观测值有两个输入特征和一个响应,如下所示:
predictors = [0 1 0 1; 0 0 1 1]; responses = [0 0 0 1];
下一节说明如何使用神经网络拟合训练网络来拟合数据集。此示例使用工具箱附带的示例数据集。
使用神经网络拟合对数据进行拟合
此示例说明如何使用神经网络拟合训练浅层神经网络来对数据进行拟合。
使用 nftool 打开神经网络拟合。
nftool
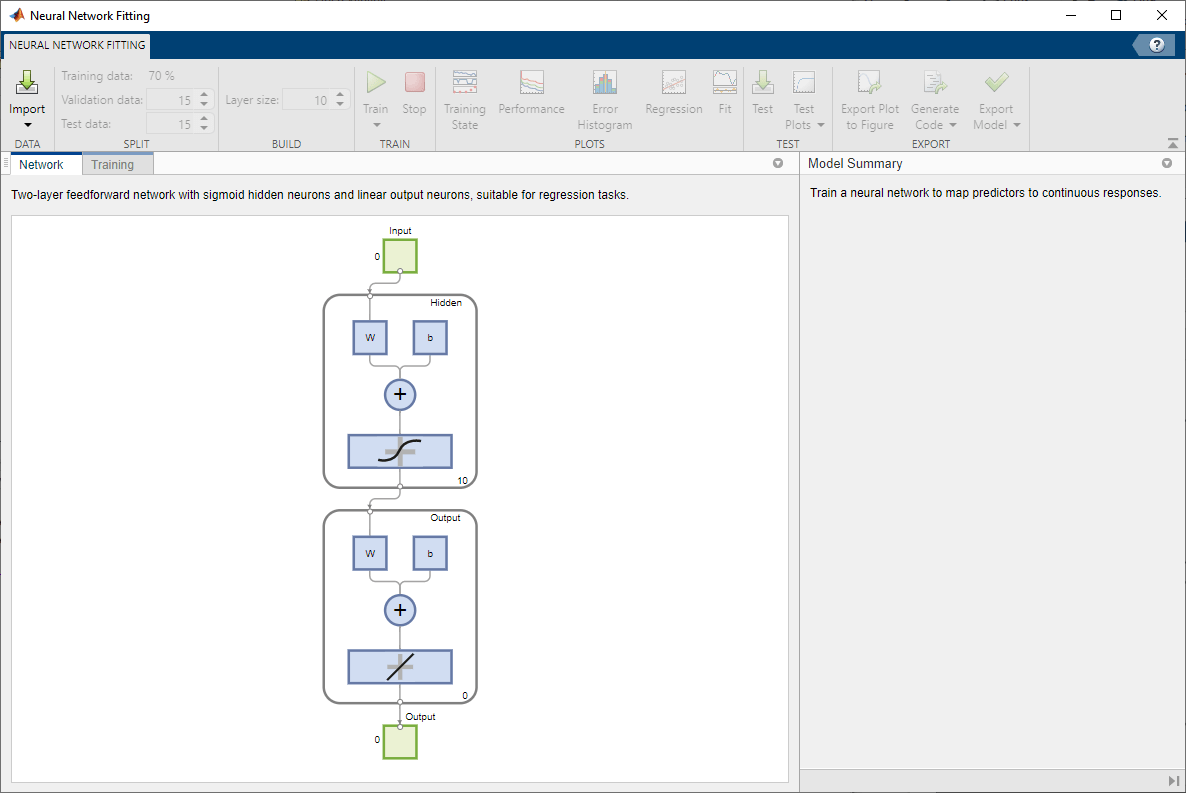
选择数据
神经网络拟合提供了示例数据来帮助您开始训练神经网络。
要导入示例体脂数据,请选择导入 > 导入体脂数据集。您可以使用此数据集来训练神经网络,以基于各种测量值来估计人的体脂。如果您从文件或工作区导入自己的数据,则必须指定预测变量和响应变量,以及观测值位于行中还是列中。
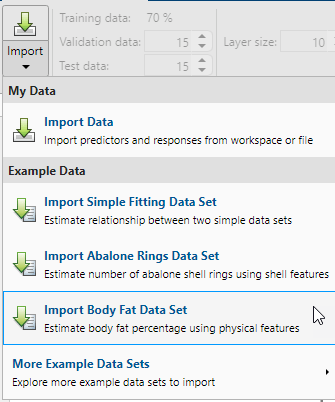
有关导入数据的信息显示在模型摘要中。此数据集包含 252 个观测值,每个观测值有 13 个特征。响应包含每个观测值的体脂百分比。

将数据分成训练集、验证集和测试集。保留默认设置。数据拆分为:
70% 用于训练。
15% 用于验证网络是否正在泛化,并在过拟合前停止训练。
15% 用于独立测试网络泛化。
有关数据划分的详细信息,请参阅划分数据以实现最优神经网络训练。
创建网络
网络是一个双层前馈网络,其中在隐藏层有一个 sigmoid 传递函数,在输出层有一个线性传递函数。层大小值定义隐藏神经元的数量。保持默认层大小值 10。您可以在网络窗格中看到网络架构。网络图会更新以反映输入数据。在此示例中,数据有 13 个输入(特征)和一个输出。

训练网络
要训练网络,请选择训练 > 莱文贝格-马夸特法训练。这是默认训练算法,与点击训练效果相同。
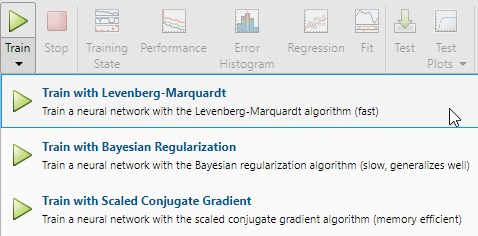
对于大多数问题,都推荐使用莱文贝格-马夸特 (trainlm) 进行训练。对于含噪问题或小型问题,贝叶斯正则化 (trainbr) 可以获得更好的解,但代价是耗时更长。对于大型问题,推荐使用量化共轭梯度 (trainscg),因为它使用的梯度计算比其他两种算法使用的雅可比矩阵计算更节省内存。
在训练窗格中,您可以看到训练进度。训练会一直持续,直到满足其中一个停止条件。在此示例中,训练会一直持续,直到六次连续验证迭代的验证误差大于或等于先前最小验证误差(“满足验证条件”)。

分析结果
模型摘要包含关于每个数据集的训练算法和训练结果的信息。
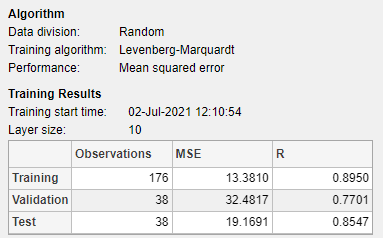
您可以通过生成绘图来进一步分析结果。要对线性回归绘图,请在绘图部分中,点击回归。回归图显示关于训练集、验证集和测试集的响应(目标)的网络预测(输出)。
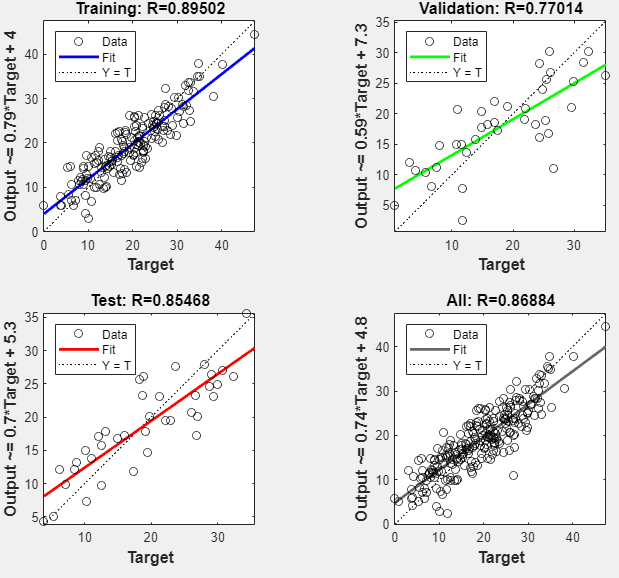
如果是完美拟合,则数据应沿 45 度线下降,其中网络输出等于响应。对于此问题,所有数据集的拟合效果都很不错。如果您需要更准确的结果,可以再次点击训练重新训练网络。每次训练都会采用不同网络初始权重和偏置,并且在重新训练后可以产生改进的网络。
查看误差直方图以获得网络性能的额外验证。在绘图部分中,点击误差直方图。

蓝条表示训练数据,绿条表示验证数据,红条表示测试数据。直方图可以指示离群值,这些离群值是拟合明显比大部分数据差的数据点。最好检查离群值以确定数据是否不良,或者这些数据点是否不同于数据集的其余部分。如果离群值是有效的数据点,但不同于其余数据,则网络将对这些点进行外插。您应该收集更多看起来像离群数据点的数据,并重新训练网络。
如果您对网络性能不满意,可以执行以下操作之一:
重新训练网络。
增加隐藏神经元的数量。
使用更大的训练数据集。
如果基于训练集的性能很好,但测试集的性能很差,这可能表明模型出现了过拟合。减少神经元的数量可以减少过拟合。
您还可以评估基于附加测试集的网络性能。要加载附加测试数据来评估网络,请在测试部分中,点击测试。模型摘要显示附加测试结果。您也可以生成图来分析附加测试数据结果。
生成代码
选择生成代码 > 生成简单的训练脚本以创建 MATLAB 代码,从命令行重现前面的步骤。如果您要了解如何使用工具箱的命令行功能来自定义训练过程,则创建 MATLAB 代码会很有帮助。在使用命令行函数拟合数据中,您可以更详细地研究生成的脚本。
导出网络
您可以将经过训练的网络导出到工作区或 Simulink®。您也可以使用 MATLAB Compiler™ 工具和其他 MATLAB 代码生成工具部署网络。要导出您的训练网络和结果,请选择导出模型 > 导出到工作区。

使用命令行函数拟合数据
了解如何使用工具箱的命令行功能的最简单方法是从 App 生成脚本,然后修改它们以自定义网络训练。例如,看一下上一节使用神经网络拟合创建的简单脚本。
% Solve an Input-Output Fitting problem with a Neural Network % Script generated by Neural Fitting app % Created 15-Mar-2021 10:48:13 % % This script assumes these variables are defined: % % bodyfatInputs - input data. % bodyfatTargets - target data. x = bodyfatInputs; t = bodyfatTargets; % Choose a Training Function % For a list of all training functions type: help nntrain % 'trainlm' is usually fastest. % 'trainbr' takes longer but may be better for challenging problems. % 'trainscg' uses less memory. Suitable in low memory situations. trainFcn = 'trainlm'; % Levenberg-Marquardt backpropagation. % Create a Fitting Network hiddenLayerSize = 10; net = fitnet(hiddenLayerSize,trainFcn); % Setup Division of Data for Training, Validation, Testing net.divideParam.trainRatio = 70/100; net.divideParam.valRatio = 15/100; net.divideParam.testRatio = 15/100; % Train the Network [net,tr] = train(net,x,t); % Test the Network y = net(x); e = gsubtract(t,y); performance = perform(net,t,y) % View the Network view(net) % Plots % Uncomment these lines to enable various plots. %figure, plotperform(tr) %figure, plottrainstate(tr) %figure, ploterrhist(e) %figure, plotregression(t,y) %figure, plotfit(net,x,t)
您可以保存脚本,然后从命令行运行它,以重现上次训练会话的结果。您还可以编辑脚本来自定义训练过程。在此例中,请遵循脚本中的每个步骤。
选择数据
该脚本假设预测变量和响应向量已加载到工作区中。如果未加载数据,您可以按如下方式加载它:
load bodyfat_dataset此命令将预测变量 bodyfatInputs 和响应变量 bodyfatTargets 加载到工作区中。
此数据集是工具箱的示例数据集之一。有关可用数据集的信息,请参阅浅层神经网络的样本数据集。您可以输入命令 help nndatasets 来查看所有可用数据集的列表。您可以使用自己的变量名称从这些数据集中加载变量。例如,命令
[x,t] = bodyfat_dataset;
会将体脂预测变量加载到数组 x 中,将体脂响应变量加载到数组 t 中。
选择训练算法
选择训练算法。网络使用默认的莱文贝格-马夸特算法 (trainlm) 进行训练。
trainFcn = 'trainlm'; % Levenberg-Marquardt backpropagation.
对于莱文贝格-马夸特无法产生期望的准确结果的问题,或对于大型数据问题,请考虑使用以下命令之一将网络训练函数设置为贝叶斯正则化 (trainbr) 或量化共轭梯度 (trainscg):
net.trainFcn = 'trainbr'; net.trainFcn = 'trainscg';
创建网络
创建一个网络。用于函数拟合(或回归)问题的默认网络 fitnet 是一个前馈网络,其默认 tan-sigmoid 传递函数在隐藏层,线性传递函数在输出层。网络有一个包含十个神经元(默认值)的隐藏层。网络有一个输出神经元,因为只有一个响应值与每个输入向量关联。
hiddenLayerSize = 10; net = fitnet(hiddenLayerSize,trainFcn);
注意
神经元越多,需要的计算也越多;当数量设置得太高时,可能会出现数据过拟合倾向,但这使网络能够求解更复杂的问题。层越多,需要的计算也越多,但使用更多的层可以使网络更高效地求解复杂问题。要使用多个隐藏层,请在 fitnet 命令中输入隐藏层大小作为数组的元素。
划分数据
设置数据划分。
net.divideParam.trainRatio = 70/100; net.divideParam.valRatio = 15/100; net.divideParam.testRatio = 15/100;
使用这些设置,预测变量向量和响应向量将被随机划分,70% 用于训练,15% 用于验证,15% 用于测试。有关数据划分过程的详细信息,请参阅划分数据以实现最优神经网络训练。
训练网络
训练网络。
[net,tr] = train(net,x,t);
在训练期间,将打开训练进度窗口。您随时可以通过点击停止按钮  来中断训练。
来中断训练。
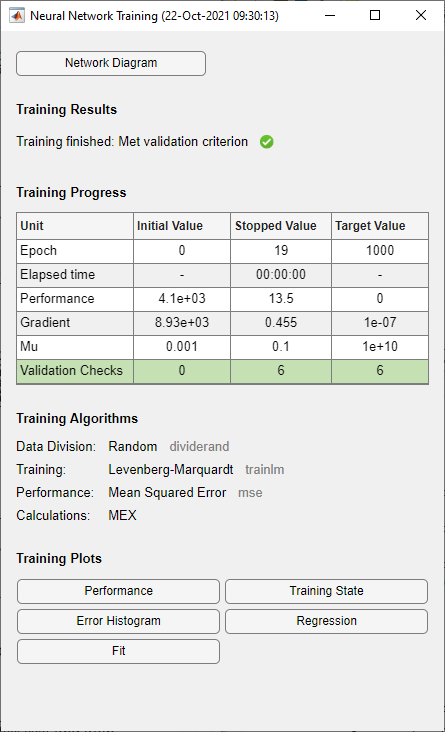
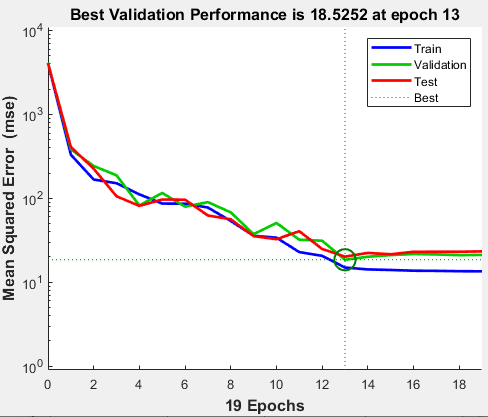
当验证误差大于或等于六次连续验证迭代的先前最小验证误差时,训练结束。如果在训练窗口中点击性能,将显示表示训练误差、验证误差和测试误差的图,如下图所示。在此示例中,结果是合理的,原因如下:
最终均方误差很小。
测试集误差和验证集误差具有相似特性。
在第 13 轮训练结束(出现最佳验证性能)前未出现明显的过拟合。
测试网络
测试网络。您可以使用经过训练的网络来计算网络输出。以下代码将计算网络输出、误差和整体性能。
y = net(x); e = gsubtract(t,y); performance = perform(net,t,y)
performance = 16.2815
通过使用训练记录中的测试索引,还可以只针对测试集计算网络性能。有关详细信息,请参阅分析训练后的浅层神经网络性能。
tInd = tr.testInd; tstOutputs = net(x(:,tInd)); tstPerform = perform(net,t(tInd),tstOutputs)
tstPerform = 20.1698
查看网络
查看网络图。
view(net)
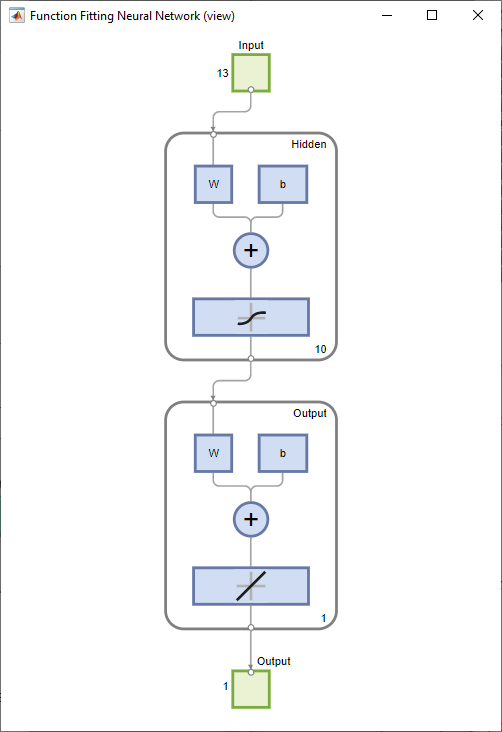
分析结果
分析得到的结果。要在网络预测(输出)和对应的响应(目标)之间执行线性回归,请在训练窗口中点击回归。
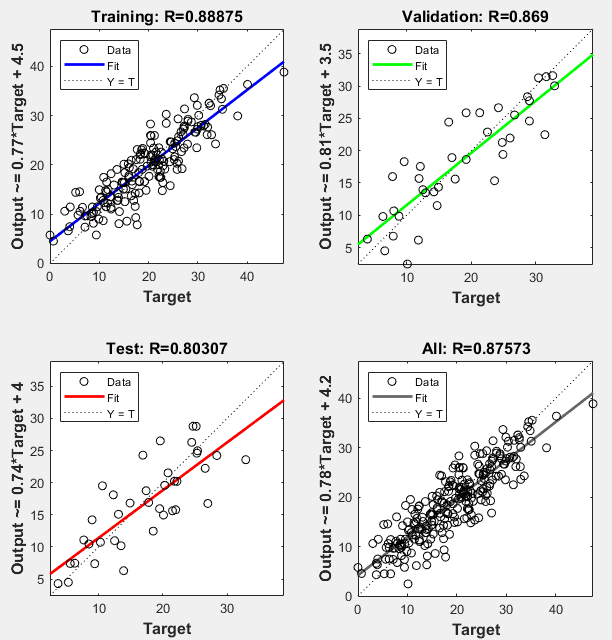
对于训练集、测试集和验证集,输出非常好地跟踪了响应,并且总数据集的 R 值超过 0.87。如果需要更准确的结果,可以尝试以下任一方法:
在此例中,网络响应是令人满意的,现在您可以将该网络用于新数据。
后续步骤
要进一步熟悉命令行操作,请尝试以下任务:
在训练期间,打开绘图窗口(如回归图),并观察其动画效果。
从命令行使用
plotfit、plotregression、plottrainstate和plotperform等函数绘图。
此外,从命令行进行训练时,可以查看高级脚本以了解更多选项。
每次训练神经网络时,由于初始权重和偏置值随机,并且将数据划分为训练集、验证集和测试集的方式也不同,可能会产生不同的解。因此,针对同一问题训练的不同神经网络对同一输入可能给出不同输出。为确保找到准确度良好的神经网络,需要多次重新训练。
如果需要更高的准确度,可以采用几种其他方法来改进初始解。有关详细信息,请参阅提高浅层神经网络泛化能力,避免过拟合。
另请参阅
神经网络拟合 | 神经网络时间序列 | 神经网络模式识别 | 神经网络聚类 | 深度网络设计器 | trainlm | fitnet