equalizeLayers

Load Pretrained Network and Data

Download the CIFAR-10 data set [1]. The data set contains 60,000 images. Each image is 32-by-32 in size and has three color channels (RGB). The size of the data set is 175 MB. Depending on your internet connection, the download process can take some time.

datadir = tempdir;
downloadCIFARData(datadir);

Downloading CIFAR-10 dataset (175 MB). This can take a while...done.

Load the trained network for CIFAR-10 using a MobileNet-v2 backbone. The batch normalization layers have been folded into the convolution and grouped convolution layers.

net = load("CIFARMobilenet.mat").net;

Load the CIFAR-10 training and test images as 4-D arrays. The training set contains 50,000 images and the test set contains 10,000 images. Create an augmentedImageDatastore object to use for network training and validation.

[XTrain,TTrain,XTest,TTest] = loadCIFARData(datadir);
inputSize = net.Layers(1).InputSize;
augimdsTrain = augmentedImageDatastore(inputSize,XTrain,TTrain);
augimdsTest  = augmentedImageDatastore(inputSize,XTest,TTest);
classes = categories(TTest);

Calculate the accuracy of the trained network on the test data.

scores = minibatchpredict(net,augimdsTest);
YTest = scores2label(scores,classes);
accuracyOfnet = mean(YTest == TTest)*100;
display("Accuracy of original network on validation data: " + accuracyOfnet + "%");

    "Accuracy of original network on validation data: 85.92%"

You can use the deepNetworkDesigner function to open the Deep Network Designer app and display the network diagram and the total number of learnable parameters in the network.

deepNetworkDesigner(net)

When you quantize then network to int8 format, it produces an accuracy of 16.8%. This is nearly a 70% degradation compared to the accuracy of the floating-point version of the network.

Analyze Network

One possible cause of major performance degradation during quantization is the significant range variation in the weight tensor of the convolution and grouped convolution layers. To investigate this variation, you can view the layer weights at the filter level for the first depth-wise separable convolution layer.

For a more detailed view, plot the weight tensor as a boxplot across filters.

layerWeights = net.Layers(4).Weights;
layerWeights = reshape(layerWeights,[9 32]);
boxchart(layerWeights)
xlabel("Filters (Groups)")
ylabel("Weight Values")
title("Weights Ranges of Original Network")

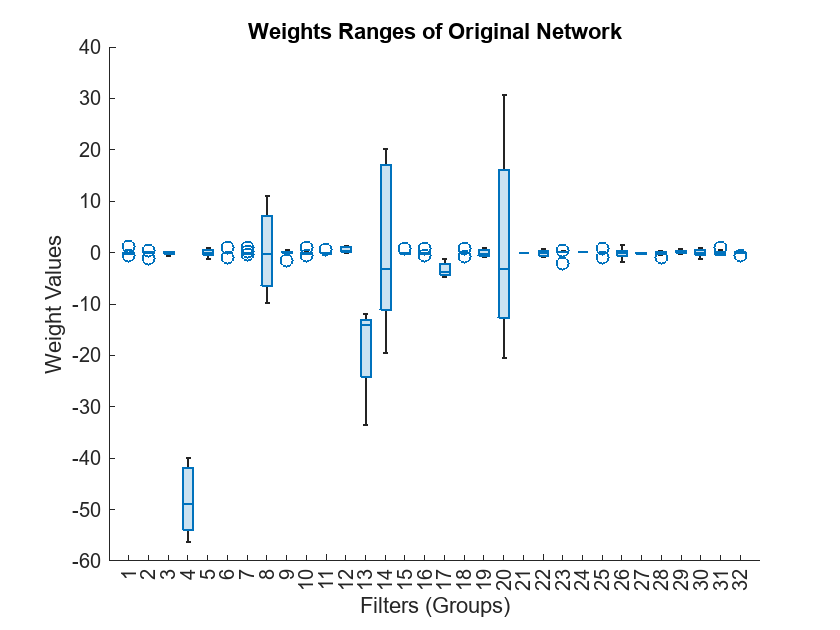
Due to the significant range variation across the filters, many filter groups are not representable after quantization to int8 format. Nonrepresentable filter groups cause severe network degradation when the error produced by nonrepresentable values propagates through the network.

To view the histogram bins across different layers, import a calibrated dlquantizer object into the Deep Network Quantizer app. The app displays histograms of the dynamic ranges of the parameters as well as the minimum and maximum values across each network layer parameter tensor. Quantization of Deep Neural Networks explains this process in detail.

Use equalizeLayers to Adjust Network Parameters

You can use the equalizeLayers function to improve the network quantization behavior. The equalizeLayers function can be used on networks that have linear activation functions that exhibit a positive scale equivariance property [1]. The equalizeLayers function tries to find compatible layers and modifies the weights to make the network more suitable for quantization. The function modifies the layer weights in such a way that the overall numerical output of the network is unchanged.

Equalize the layers in the network.

equalizedNet = equalizeLayers(net);

Quantize Equalized Network

After you equalize the layers, quantize the network. Compare the accuracy of the quantized network with and without equalized layers.

Create a dlquantizer object for the equalized network.

dlQuantObj = dlquantizer(equalizedNet);

Define calibration data to use for quantization.

numberOfCalibrationImages = 500;
augimdsCalibration = subset(augimdsTrain,1:numberOfCalibrationImages);

Calibrate the dlquantizer object.

calibStats = calibrate(dlQuantObj,augimdsCalibration)

calibStats=157×5 table
          Optimized Layer Name               Network Layer Name         Learnables / Activations    MinValue    MaxValue
    _________________________________    ___________________________    ________________________    ________    ________

    "Conv1_Weights"                      {'Conv1'                  }           "Weights"             -1.9843     1.5405 
    "Conv1_Bias"                         {'Conv1'                  }           "Bias"                -5.8864     4.7606 
    "expanded_conv_depthwise_Weights"    {'expanded_conv_depthwise'}           "Weights"             -2.1183     1.5631 
    "expanded_conv_depthwise_Bias"       {'expanded_conv_depthwise'}           "Bias"                -2.3202     4.1318 
    "expanded_conv_project_Weights"      {'expanded_conv_project'  }           "Weights"             -2.1404     1.9959 
    "expanded_conv_project_Bias"         {'expanded_conv_project'  }           "Bias"                -9.1792     10.327 
    "block_1_expand_Weights"             {'block_1_expand'         }           "Weights"            -0.85797     1.1262 
    "block_1_expand_Bias"                {'block_1_expand'         }           "Bias"                -2.2402     4.8886 
    "block_1_depthwise_Weights"          {'block_1_depthwise'      }           "Weights"             -1.5857     2.3307 
    "block_1_depthwise_Bias"             {'block_1_depthwise'      }           "Bias"                -8.9999     9.0277 
    "block_1_project_Weights"            {'block_1_project'        }           "Weights"             -3.9702     2.3751 
    "block_1_project_Bias"               {'block_1_project'        }           "Bias"                -15.641     17.965 
    "block_2_expand_Weights"             {'block_2_expand'         }           "Weights"            -0.41095    0.36931 
    "block_2_expand_Bias"                {'block_2_expand'         }           "Bias"                -2.1926      4.034 
    "block_2_depthwise_Weights"          {'block_2_depthwise'      }           "Weights"               -2.06     2.1283 
    "block_2_depthwise_Bias"             {'block_2_depthwise'      }           "Bias"                -2.2893     4.5481 
      ⋮

Use the quantize function to create a simulatable quantized network from the dlquantizer object.

qNetEqualized = quantize(dlQuantObj);

Evaluate the accuracy of the quantized network. The table compares the accuracy of the original floating-point network, the quantized network without equalized layers, and the quantized network with equalized layers.

qscores = minibatchpredict(qNetEqualized,augimdsTest);
YTest = scores2label(qscores,classes);
accuracyOfQuantizedNet = mean(YTest == TTest)*100;
createComparisonTable(accuracyOfnet,accuracyOfQuantizedNet)

ans=1×3 table
                              Original Network    Quantized Original Network    Quantized Equalized Network
                              ________________    __________________________    ___________________________

    Test Data Accuracy (%)         85.92                    16.81                          76.63           

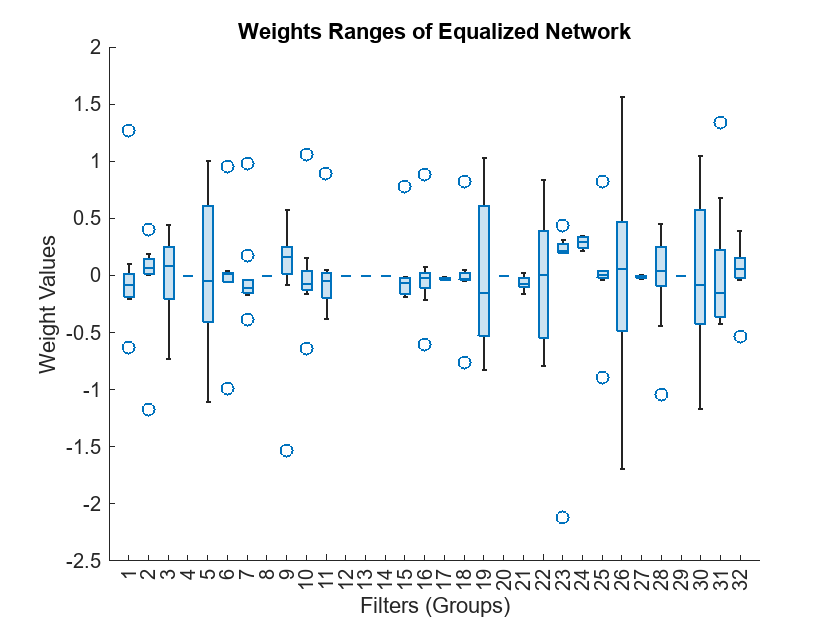
Plot the new weight tensor as a boxplot across the filters. The weight ranges for the equalized network are better distributed and the quantized equalized network performance is significantly better than the quantized network without layer equalization.

newLayerWeights = equalizedNet.Layers(4).Weights;
newLayerWeights = reshape(newLayerWeights,[9 32]);
boxchart(newLayerWeights)
xlabel("Filters (Groups)")
ylabel("Weight Values")
title("Weights Ranges of Equalized Network")

Helper Functions

The createComparisonTable helper function prints a table comparing the accuracy of the original floating-point network, the quantized network without equalized layers, and the quantized network with equalized layers.

function comparisonTable = createComparisonTable(originalAccuracy,accuracyQuantizedEqualizedNet)
% Create the summary table
comparisonTable = table(originalAccuracy,16.81,accuracyQuantizedEqualizedNet, ...
    VariableNames=["Original Network", "Quantized Original Network", "Quantized Equalized Network"], ...
    RowNames="Test Data Accuracy (%)");
end