estimate

Estimate posterior distribution of Bayesian nonlinear non-Gaussian state-space model parameters

Since R2024b

Syntax

PosteriorMdl = estimate(PriorMdl,Y,params0)

PosteriorMdl = estimate(PriorMdl,Y,params0,Name=Value)

[PosteriorMdl,estParams,EstParamCov,Summary]
= estimate(___)

Description

PosteriorMdl = estimate(PriorMdl,Y,params0) returns the posterior Bayesian nonlinear state-space model PosteriorMdl from combining the Bayesian nonlinear state-space model prior distribution and likelihood PriorMdl with the response data Y. The input argument params0 is the vector of initial values for the unknown state-space model parameters Θ in PriorMdl.

estimate obtains the posterior samples by using a combination of Markov chain Monte Carlo (MCMC), sequential Monte Carlo (SMC), pseudo-marginal, and particle-marginal Metropolis-Hastings (MH) methods. estimate obtains a nonnegative and unbiased estimator of the likelihood function from the importance weights.

example

PosteriorMdl = estimate(PriorMdl,Y,params0,Name=Value) specifies additional options using one or more name-value arguments. For example, estimate(PriorMdl,Y,params0,NumDraws=1e3,Thin=4,DoF=10) uses the multivariate t₁₀ distribution for the MH proposal [6][8], draws 4e3 random vectors of parameters, and thins the sample to reduce serial correlation by discarding every 3 draws until it retains 1e3 draws.

example

[PosteriorMdl,estParams,EstParamCov,Summary] = estimate(___) additionally returns the following quantities using any of the input-argument combinations in the previous syntaxes:

estParams — A vector containing the estimated parameters Θ.
EstParamCov — The estimated variance-covariance matrix of the estimated parameters Θ.
Summary — Estimation summary of the posterior distribution of parameters Θ.

example

Examples

collapse all

Estimate Posterior Distribution

Open Live Script

This example estimates the posterior distribution of the Bayesian nonlinear state-space model in equation. The example uses simulated data.

$\begin{array}{l} x_{t} = ϕ x_{t - 1} + σ u_{t} \\ y_{t} \sim P o i s s o n (λ e^{x_{t}}), \end{array}$

where the parameters in $Θ = {ϕ, σ, λ}$ have the following priors:

$ϕ \sim N_{(- 1, 1)} (m_{0}, v_{0}^{2})$ , that is, a truncated normal distribution with $ϕ \in [- 1, 1]$ .
$σ^{2} \sim IG (a_{0}, b_{0})$ , that is, an inverse gamma distribution with shape $a_{0}$ and scale $b_{0}$ .
$λ \sim Gamma (α_{0}, β_{0})$ , that is, a gamma distribution with shape $α_{0}$ and scale $β_{0}$ .

To estimate the posterior distribution, the estimate function requires response data, a bnlssm object that specifies the prior distribution and identifies which parameters to fit to the data, and initial values for the estimable parameters.

Simulate Series

Consider this data-generating process (DGP).

$\begin{array}{l} x_{t} = 0.7 x_{t - 1} + \sqrt{0.2} u_{t} \\ y_{t} \sim P o i s s o n (3 e^{x_{t}}), \end{array}$

where the series $u_{t}$ is a standard Gaussian series of random variables.

Simulate a series of 200 observations from the process.

rng(1,"twister")    % For reproducibility
T = 200;
thetaDGP = [0.7; 0.2; 3];

numparams = numel(thetaDGP);

MdlXSim = arima(AR=thetaDGP(1),Variance=thetaDGP(2), ...
    Constant=0);
xsim = simulate(MdlXSim,T);
y = random("poisson",thetaDGP(3)*exp(xsim));

figure
plot(y)

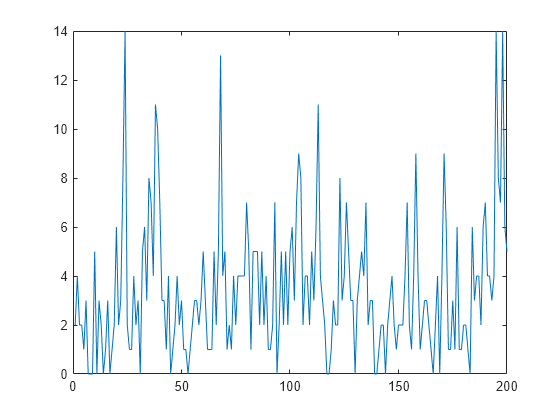
Figure contains an axes object. The axes object contains an object of type line.

Create Bayesian Nonlinear Prior Model

A prior distribution is required to compose a posterior distribution. The Local Functions section contains the functions paramMap and priorDistribution required to specify the Bayesian nonlinear state-space model. The paramMap function specifies the state-space model structure and initial state moments. The priorDistribution function returns the log of the joint prior distribution of the state-space model parameters. You can use the functions only within this script.

Create a Bayesian nonlinear state-space model for the DGP.

Arbitrarily choose values for the hyperparameters.
Indicate that the state-space model observation equation is expressed as a distribution.
To speed up computations, the arguments A and LogY of the paramMap function are written to enable simultaneous evaluation of the transition and observation densities of multiple particles. Specify this characteristic by using the Multipoint name-value argument.

% pi(phi,sigma2) hyperparameters
m0 = 0;                 
v02 = 1;
a0 = 1;
b0 = 1;

% pi(lambda) hyperparameters
alpha0 = 3;
beta0 = 1;

hyperparams = [m0 v02 a0 b0 alpha0 beta0];

PriorMdl = bnlssm(@paramMap,@(x)priorDistribution(x,hyperparams), ...
    ObservationForm="distribution",Multipoint=["A" "LogY"]);

PriorMdl is a bnlssm model specifying the state-space model structure and prior distribution of the state-space model parameters. Because PriorMdl contains unknown values, it serves as a template for posterior estimation with observations.

Choose Initial Parameter Values

Arbitrarily choose a set of initial parameter for the MCMC sampler.

theta0 = [0.5; 0.1; 2];

Estimate Posterior

Estimate the posterior by passing the prior model, simulated data, and initial parameter values to estimate.

PosteriorMdl = estimate(PriorMdl,y,theta0);

         Optimization and Tuning        
      | Params0  Optimized  ProposalStd 
----------------------------------------
 c(1) |  0.5000    0.6081      0.0922   
 c(2) |  0.1000    0.2190      0.0503   
 c(3) |   2        2.8497      0.2918   
 
     Posterior Distributions of Parameters     
      |  Mean     Std   Quantile05  Quantile95 
-----------------------------------------------
 c(1) | 0.6046  0.0897    0.4467      0.7223   
 c(2) | 0.2412  0.0528    0.1636      0.3380   
 c(3) | 2.9481  0.2950    2.4732      3.4146   

    Posterior Distributions of Final States    
      |  Mean     Std   Quantile05  Quantile95 
-----------------------------------------------
 x(1) | 0.4736  0.3618    -0.1050     1.0760   
Proposal acceptance rate = 42.10%

PosteriorMdl.ParamMap

ans = function_handle with value:
    @paramMap

ThetaPostDraws = PosteriorMdl.ParamDistribution;
[numParams,numDraws] = size(ThetaPostDraws)

numParams = 
3

numDraws = 
1000

estimate finds an optimal proposal distribution for the MCMC sampler by using the tune function, and prints the optimal moments to the command line. estimate also displays a summary of the posterior distribution of the parameters. The true values of the parameters are close to their corresponding posterior means; all are within their corresponding 95% credible intervals.

PosteriorMdl is a bnlssm object representing the posterior distribution.

PosteriorMdl.ParamMap is the function handle to the function representing the state-space model structure; it is the same function as PrioirMdl.ParamMap.
ThetaPostDraws is a 3-by-1000 matrix of draws from the posterior distribution. By default, estimate treats the first 100 draws as a burn-in sample and excludes them from the results.

To diagnose the MCMC sampler, create trace plots of the posterior parameter draws.

paramnames = ["\phi" "\sigma^2" "\lambda"];

figure
h = tiledlayout(3,1);
for j = 1:numParams
    nexttile
    plot(ThetaPostDraws(j,:))
    hold on
    yline(thetaDGP(j))
    ylabel(paramnames(j))
end
title(h,"Posterior Trace Plots")

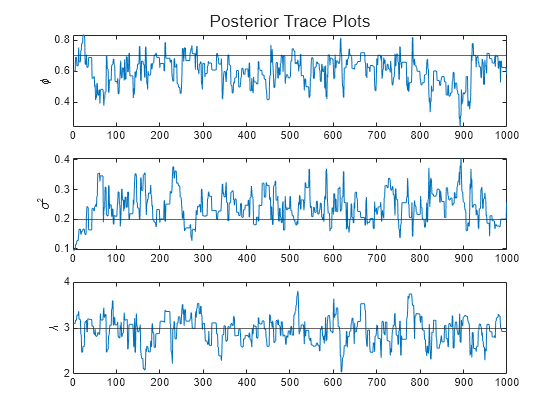
$Figure contains 3 axes objects. Axes object 1 with ylabel \phi contains 2 objects of type line, constantline. Axes object 2 with ylabel \sigma^2 contains 2 objects of type line, constantline. Axes object 3 with ylabel \lambda contains 2 objects of type line, constantline.$

The sampler eventually settles at near the true values of the parameters. In this case, the sample shows serial correlation and transient behavior. You can remedy serial correlation in the sample by adjusting the Thin name-value argument, and you can remedy transient effects by increasing the burn-in period using the BurnIn name-value argument.

Local Functions

These functions specify the state-space model parameter mappings, in distribution form, and the log prior distribution of the parameters.

function [A,B,LogY,Mean0,Cov0,StateType] = paramMap(theta)
    A = theta(1); 
    B = sqrt(theta(2));
    LogY = @(y,x)y.*(x + log(theta(3)))- exp(x).*theta(3);
    Mean0 = 0;
    Cov0 = 2;
    StateType = 0;     % Stationary state process
end

function logprior = priorDistribution(theta,hyperparams)
    % Prior of phi
    m0 = hyperparams(1);
    v20 = hyperparams(2);
    pphi = makedist("normal",mu=m0,sigma=sqrt(v20));
    pphi = truncate(pphi,-1,1);
    lpphi = log(pdf(pphi,theta(1)));

    % Prior of sigma2
    a0 = hyperparams(3);
    b0 = hyperparams(4);
    lpsigma2 = -a0*log(b0) - log(gamma(a0)) + (-a0-1)*log(theta(2)) - ...
        1./(b0*theta(2));

    % Prior of lambda
    alpha0 = hyperparams(5);
    beta0 = hyperparams(6);
    plambda = makedist("gamma",alpha0,beta0);
    lplambda = log(pdf(plambda,theta(3))); 

    logprior = lpphi + lpsigma2 + lplambda;
end

Improve Markov Chain Convergence

Open Live Script

Consider the model in the example Estimate Posterior Distribution. Improve the Markov chain convergence by adjusting sampler options.

Create a Bayesian nonlinear state-space model (bnlssm) object that represents the DGP, and then simulate a response path.

rng(1,"twister")    % For reproducibility
T = 200;
thetaDGP = [0.7; 0.2; 3];

numparams = numel(thetaDGP);

MdlXSim = arima(AR=thetaDGP(1),Variance=thetaDGP(2), ...
    Constant=0);
xsim = simulate(MdlXSim,T);
y = random("poisson",thetaDGP(3)*exp(xsim));

Create the Bayesian nonlinear state-space model template for estimation by passing function handles directly to paramMap and paramDistribution to bnlssm (the functions are in Local Functions).

m0 = 0;
v02 = 1;
a0 = 1;
b0 = 1;
alpha0 = 3;
beta0 = 1;
hyperparams = [m0 v02 a0 b0 alpha0 beta0];

PriorMdl = bnlssm(@paramMap,@(x)priorDistribution(x,hyperparams), ...
    ObservationForm="distribution",Multipoint=["A" "LogY"]);

In Estimate Posterior Distribution:

The optimized proposal moments appear adequate. Therefore, you might not need to adjust the proposal tuning procedure.
The trace plots suggest that the Markov chain settles after 100 processed draws, and significant autocorrelation among the draws exists. Therefore, you should tune the MCMC sampler.

Tune the sampler the following ways:

Because the default burn-in period is 100 draws, specify a burn-in period of 200 (BurnIn=200).
Specify thinning the sample by keeping the first draw of each set of 10 successive draws (Thin=10).
Retain 2000 random parameter vectors (NumDraws=2000).
Set the proposal scale proportionality constant to 0.25 to increase the sample acceptance rate.

Estimate the posterior distribution. Specify the simulated response path as observed responses, an arbitrary set of initial parameter values to initialize the MCMC algorithm, and the settings to tune the sampler.

theta0 = [0.5; 0.1; 2]; 

PosteriorMdl = estimate(PriorMdl,y,theta0,Burnin=200,Thin=10, ...
    NumDraws=2000,Proportion=0.25);

         Optimization and Tuning        
      | Params0  Optimized  ProposalStd 
----------------------------------------
 c(1) |  0.5000    0.6081      0.0922   
 c(2) |  0.1000    0.2190      0.0503   
 c(3) |   2        2.8497      0.2918   
 
     Posterior Distributions of Parameters     
      |  Mean     Std   Quantile05  Quantile95 
-----------------------------------------------
 c(1) | 0.6001  0.0984    0.4304      0.7504   
 c(2) | 0.2410  0.0536    0.1644      0.3394   
 c(3) | 2.8777  0.2918    2.4208      3.3894   

    Posterior Distributions of Final States    
      |  Mean     Std   Quantile05  Quantile95 
-----------------------------------------------
 x(1) | 0.4860  0.3713    -0.1416     1.0723   
Proposal acceptance rate = 68.60%

ThetaPostDraws = PosteriorMdl.ParamDistribution;

Plot trace plots and correlograms of the parameters.

paramnames = ["\phi" "\sigma^2" "\lambda"];

figure
h = tiledlayout(numparams,1);
for j = 1:numparams
    nexttile
    plot(ThetaPostDraws(j,:))
    hold on
    yline(thetaDGP(j))
    ylabel(paramnames(j))
end
title(h,"Posterior Trace Plots")

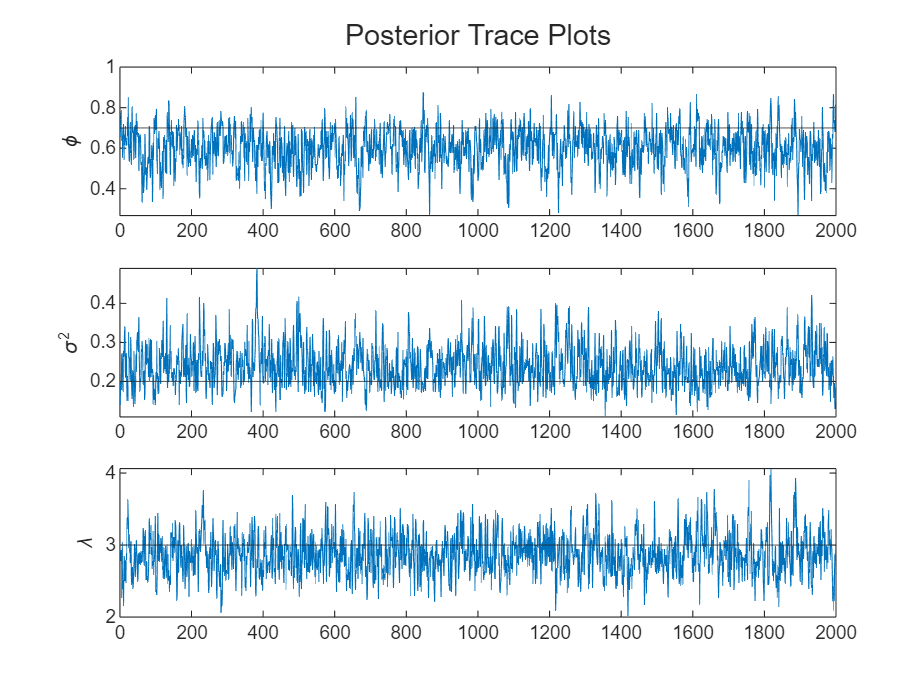
figure
h = tiledlayout(numparams,1);
for j = 1:numparams
    nexttile
    autocorr(ThetaPostDraws(j,:));
    ylabel(paramnames(j));
    title([]);
end
title(h,"Posterior Sample Correlograms")

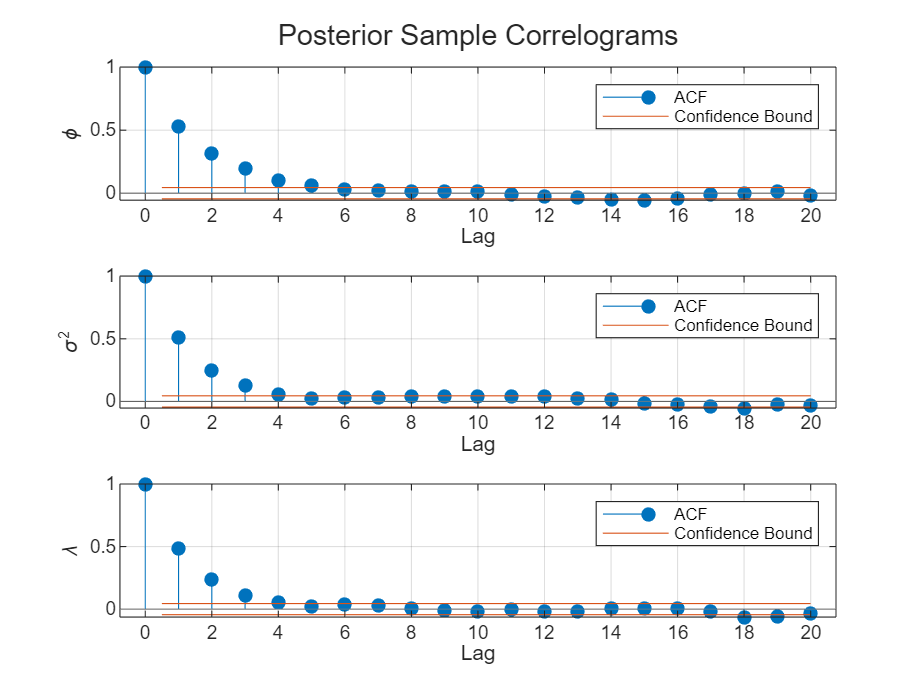
The sampler quickly settles near the true values of the parameters. The sample shows little serial correlation and no transient behavior.

Create a posterior model by setting the parameter distribution property of the prior model (ParamDistribution) to the posterior draws. Compute posterior means of each parameter.

PosteriorMdl = PriorMdl;
PosteriorMdl.ParamDistribution = ThetaPostDraws;
estParams = mean(ThetaPostDraws);

Use the posterior distribution to compute smoothed and filtered states, and then compute fitted values by transforming estimated state series to an observation series, which represents the series of Poisson means. Compare the means and the observed series.

figure
xhats = smooth(PosteriorMdl,y,estParams);
xhatf = filter(PosteriorMdl,y,estParams);
yhats = estParams(3)*exp(xhats);
yhatf = estParams(3)*exp(xhatf);
plot([y yhatf yhats])
title("Data and Posterior Fitted Values")
ylabel("y")
legend("Observed responses","Filter-derived responses", ...
    "Smooth-derived responses")

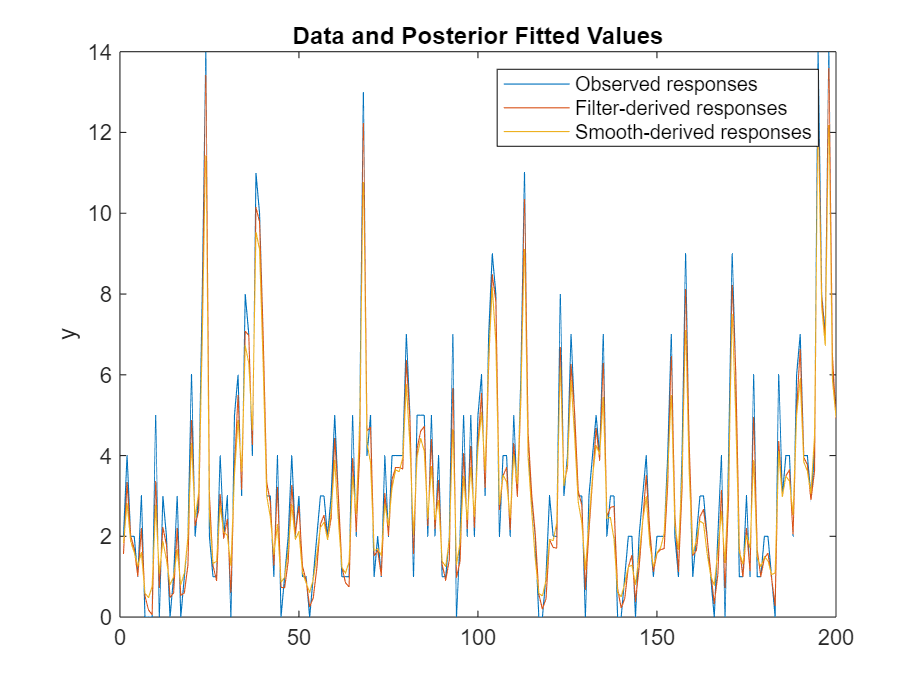
Local Functions

These functions specify the state-space model parameter mappings, in distribution form, and the log prior distribution of the parameters.

function [A,B,LogY,Mean0,Cov0,StateType] = paramMap(theta)
    A = theta(1); 
    B = sqrt(theta(2));
    LogY = @(y,x)y.*(x + log(theta(3)))- exp(x).*theta(3);
    Mean0 = 0;
    Cov0 = 2;
    StateType = 0;     % Stationary state process
end

function logprior = priorDistribution(theta,hyperparams)
    % Prior of phi
    m0 = hyperparams(1);
    v20 = hyperparams(2);
    pphi = makedist("normal",mu=m0,sigma=sqrt(v20));
    pphi = truncate(pphi,-1,1);
    lpphi = log(pdf(pphi,theta(1)));

    % Prior of sigma2
    a0 = hyperparams(3);
    b0 = hyperparams(4);
    lpsigma2 = -a0*log(b0) - log(gamma(a0)) + (-a0-1)*log(theta(2)) - ...
        1./(b0*theta(2));

    % Prior of lambda
    alpha0 = hyperparams(5);
    beta0 = hyperparams(6);
    plambda = makedist("gamma",alpha0,beta0);
    lplambda = log(pdf(plambda,theta(3))); 

    logprior = lpphi + lpsigma2 + lplambda;
end

Return Posterior Moments and Inferences

Open Live Script

Consider the model in the example Estimate Posterior Distribution.

Create a Bayesian nonlinear state-space model (bnlssm) object that represents the DGP, and then simulate a response path.

rng(1,"twister")    % For reproducibility
T = 200;
thetaDGP = [0.7; 0.2; 3];

numparams = numel(thetaDGP);

MdlXSim = arima(AR=thetaDGP(1),Variance=thetaDGP(2), ...
    Constant=0);
xsim = simulate(MdlXSim,T);
y = random("poisson",thetaDGP(3)*exp(xsim));

m0 = 0;
v02 = 1;
a0 = 1;
b0 = 1;
alpha0 = 3;
beta0 = 1;
hyperparams = [m0 v02 a0 b0 alpha0 beta0];

PriorMdl = bnlssm(@paramMap,@(x)priorDistribution(x,hyperparams), ...
    ObservationForm="distribution",Multipoint=["A" "LogY"]);

The plots in Estimate Posterior Distribution suggest that the Markov chain settles after 100 processed draws. Tune the sampler the following ways:

Because the default burn-in period is 100 draws, specify a burn-in period of 200 (BurnIn=200).
Specify thinning the sample by keeping the first draw of each set of 10 successive draws (Thin=10).
Set the proposal scale proportionality constant to 0.25 to increase the sample acceptance rate.

theta0 = [0.5; 0.1; 2]; 

[PosteriorMdl,estParams,EstParamCov,Summary] = estimate(PriorMdl,y,theta0,Burnin=200,Thin=10, ...
    Proportion=0.25);

         Optimization and Tuning        
      | Params0  Optimized  ProposalStd 
----------------------------------------
 c(1) |  0.5000    0.6081      0.0922   
 c(2) |  0.1000    0.2190      0.0503   
 c(3) |   2        2.8497      0.2918   
 
     Posterior Distributions of Parameters     
      |  Mean     Std   Quantile05  Quantile95 
-----------------------------------------------
 c(1) | 0.5954  0.0981    0.4286      0.7451   
 c(2) | 0.2429  0.0538    0.1660      0.3361   
 c(3) | 2.8609  0.2815    2.3941      3.3617   

    Posterior Distributions of Final States    
      |  Mean     Std   Quantile05  Quantile95 
-----------------------------------------------
 x(1) | 0.4911  0.3752    -0.1284     1.0801   
Proposal acceptance rate = 68.07%

Display the posterior moments

estParams

estParams = 3×1

    0.5954
    0.2429
    2.8609

EstParamCov

EstParamCov = 3×3

    0.0096   -0.0024   -0.0016
   -0.0024    0.0029   -0.0024
   -0.0016   -0.0024    0.0792

Summary

Summary=4×4 table
           Mean        Std       Quantile05    Quantile95
          _______    ________    __________    __________

    c1    0.59542    0.098059      0.42863       0.7451  
    c2    0.24291    0.053841      0.16603      0.33607  
    c3     2.8609     0.28146       2.3941       3.3617  
    x1    0.49106     0.37517     -0.12836       1.0801

estParams is the posterior mean of each parameter ordered by the elements of theta, EstParamCov is the corresponding covariance matrix, and Summary is a table of containing the moments and 95% percentile intervals based on the posterior sample. Rows c1 through c3 correspond to the parameters of theta and x1 corresponds to the first state.

You can measure the performance of the MCMC sampler by comparing the observed response series when the fitted response series, which is the time-varying mean of the Poisson distribution derived from filtered or smoothed state estimates. Symbolically, $\hat{y} = λ e^{{\hat{x}}_{t}}$ .

figure
xhats = smooth(PosteriorMdl,y,estParams);
xhatf = filter(PosteriorMdl,y,estParams);
yhats = estParams(3)*exp(xhats);
yhatf = estParams(3)*exp(xhatf);
plot([y yhatf yhats])
title("Data and Posterior Fitted Values")
ylabel("y")
legend("Observed responses","Filter-derived responses", ...
    "Smooth-derived responses")

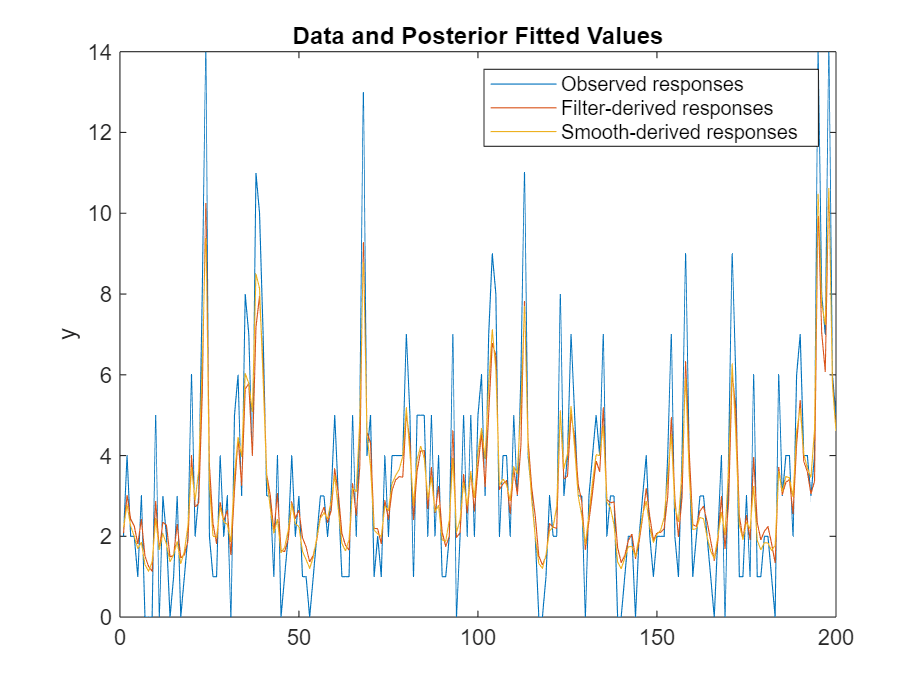
The fitted response series derived from the filtered and smoothed states follow the observed series quite well. As expected, the filtered series is less volatile than than the observed series, and the smoothed series is less volatile than the filtered series.

You can visualize the posterior distribution of the fitted response series by drawing a Monte Carlo sample from the posterior distribution of the states, and then summarizing it.

Use the simulation smoother simsmooth to draw a Monte Carlo samples from the posterior distribution of the states. For each time t, compute the sample mean and 95% percentile interval. Plot the results.

figure
xhatss = simsmooth(PosteriorMdl,y,estParams,NumPaths=1000);
yhatss = estParams(3)*squeeze(exp(xhatss));
yhatpostdesc = [mean(yhatss,2) quantile(yhatss,[0.025 0.975],2)];
h1 = plot(yhatss,Color=[0.5 0.5 0.5]);
hold on
h2 = plot(y,LineWidth=2);
h3 = plot(yhatpostdesc(:,1),"y--",LineWidth=2);
h4 = plot(yhatpostdesc(:,2:3),"c--");
title("Posterior Distribution of Fitted Values")
ylabel("y")
legend([h1(1) h2 h3 h4(1)],["Simulated response paths", ...
    "Observed responses","Posterior mean","Posterior 95% confidence bounds"])
hold off

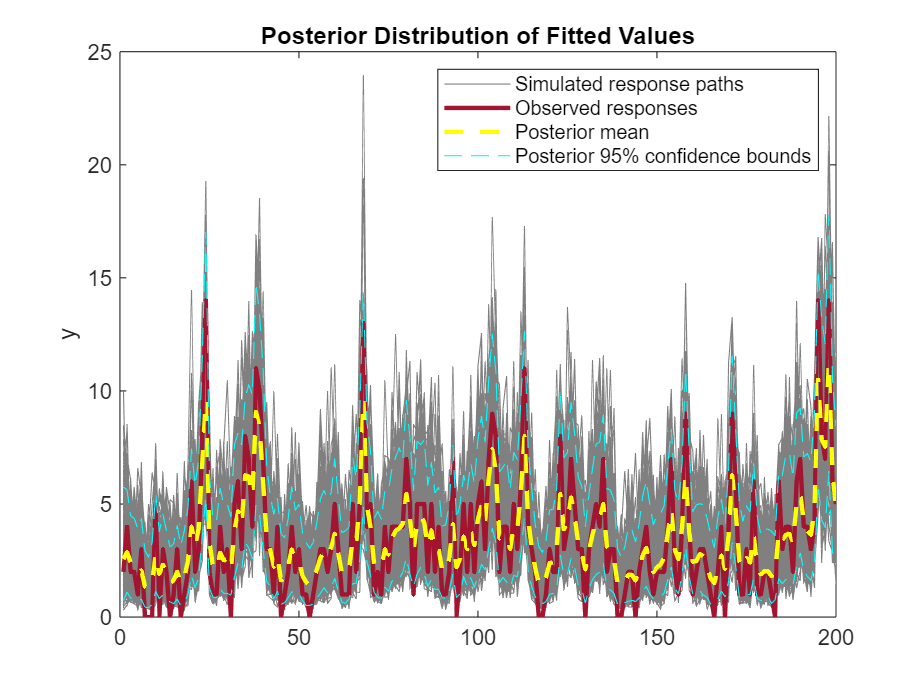
Local Functions

These functions specify the state-space model parameter mappings, in distribution form, and the log prior distribution of the parameters.

function [A,B,LogY,Mean0,Cov0,StateType] = paramMap(theta)
    A = theta(1); 
    B = sqrt(theta(2));
    LogY = @(y,x)y.*(x + log(theta(3)))- exp(x).*theta(3);
    Mean0 = 0;
    Cov0 = 2;
    StateType = 0;     % Stationary state process
end

function logprior = priorDistribution(theta,hyperparams)
    % Prior of phi
    m0 = hyperparams(1);
    v20 = hyperparams(2);
    pphi = makedist("normal",mu=m0,sigma=sqrt(v20));
    pphi = truncate(pphi,-1,1);
    lpphi = log(pdf(pphi,theta(1)));

    % Prior of sigma2
    a0 = hyperparams(3);
    b0 = hyperparams(4);
    lpsigma2 = -a0*log(b0) - log(gamma(a0)) + (-a0-1)*log(theta(2)) - ...
        1./(b0*theta(2));

    % Prior of lambda
    alpha0 = hyperparams(5);
    beta0 = hyperparams(6);
    plambda = makedist("gamma",alpha0,beta0);
    lplambda = log(pdf(plambda,theta(3))); 

    logprior = lpphi + lpsigma2 + lplambda;
end

Estimate Posterior of Stochastic Volatility Model

Open Live Script

Estimate the posterior distribution of a Bayesian nonlinear stochastic volatility model for daily S&P 500 closing returns. For a full exposition of this problem, see Fit Bayesian Stochastic Volatility Model to S&P 500 Volatility.

Consider the nonlinear state-space form of the stochastic volatility model for observed asset returns $y_{t}$ :

$\begin{array}{l} x_{t + Δ t} = α + β x_{t} + σ u_{t} \\ y_{t} = e x p (\frac{1}{2} x_{t}) \sqrt{Δ t} ε_{t}, \end{array}$

where:

$Δ t = \frac{1}{365}$ for daily returns.
$x_{t}$ is a latent AR(1) process representing the conditional volatility series.
$u_{t}$ are $ε_{t}$ are mutually independent and individually iid random standard Gaussian noise series.

The linear state-space coefficient matrices are:

$A = [\begin{array}{c} β & α \\ 0 & 1 \end{array}] .$
$B = [\begin{array}{c} σ \\ 0 \end{array}] .$

The observation equation is nonlinear. Because $ε_{t}$ is a standard Gaussian random variable, the conditional distribution of $y_{t}$ given $x_{t}$ and the parameters is Gaussian with a mean of 0 and standard deviation $\sqrt{Δ t} \exp (0.5 x_{t})$ .

Load the data set Data_GlobalIdx1.mat, and then extract the S&P 500 closing prices (last column of the matrix Data).

load Data_GlobalIdx1
sp500 = Data(:,end);
T = numel(sp500);
dts = datetime(dates,ConvertFrom="datenum");

Convert the price series to returns, and then center the returns.

retsp500 = price2ret(sp500);
y = retsp500 - mean(retsp500);
retdts = dts(2:end);

The local function paramMap, which uses the distribution form for the observation equation, specifies this model structure. Unlike the parameter mapping function in Fit Bayesian Stochastic Volatility Model to S&P 500 Volatility, paramMap reduces the number of states to one for computational efficiency.

Assume a flat prior, that is, the log prior is 0 over the support of the parameters and -Inf everywhere else. The local function flatLogPrior specifies the prior.

Create a Bayesian nonlinear state-space model that specifies the model structure and prior distribution. Specify that the observation equation is in distribution form and that bnlssm functions can evaluate multiple particles simultaneously for A and LogY.

PriorMdl = bnlssm(@paramMap,@flatLogPrior,ObservationForm="distribution", ...
    Multipoint=["A" "LogY"]);

Estimate the posterior distribution. Specify an arbitrarily chosen set of initial parameter values. Specify the following proposal-tuning settings:

Set the search interval for $β$ to (-1,1). Specified search intervals apply only to tuning the proposal.
Set the search interval for $σ$ to (0, $\infty$ ).
Specify computing the Hessian by the outer product of gradients.
For computational speed, do not sort the particles by using Hilbert sorting.

For the MCMC sampler, specify a burn-in period of 1e4 and retain every 25th draw to reduce serial correlation among the draws. The sampler, with these settings, takes some time to complete.

theta0 = [0.2 0 0.5];
lower = [-1; -Inf; 0];
upper = [1; Inf; Inf];
burnin = 1e4;
thin = 25;

rng(1)
PosteriorMdl = estimate(PriorMdl,y,theta0,Lower=lower,Upper=upper, ...
    NumParticles=500,Hessian="opg",SortParticles=false,BurnIn=burnin,Thin=thin);

         Optimization and Tuning        
      | Params0  Optimized  ProposalStd 
----------------------------------------
 c(1) |  0.2000    0.9949      0.0030   
 c(2) |   0       -0.0155      0.0116   
 c(3) |  0.5000    0.1495      0.0130   
 
      Posterior Distributions of Parameters     
      |   Mean     Std   Quantile05  Quantile95 
------------------------------------------------
 c(1) |  0.9874  0.0041     0.9800      0.9934  
 c(2) | -0.0452  0.0148    -0.0726     -0.0226  
 c(3) |  0.1460  0.0184     0.1179      0.1772  

     Posterior Distributions of Final States    
      |   Mean     Std   Quantile05  Quantile95 
------------------------------------------------
 x(1) | -3.4996  0.4214    -4.1796     -2.7654  
Proposal acceptance rate = 26.93%

Determine the quality of the posterior sample by plotting trace plots of the parameter draws.

figure
plot(PosteriorMdl.ParamDistribution(1,:))
title("Trace Plot: \beta")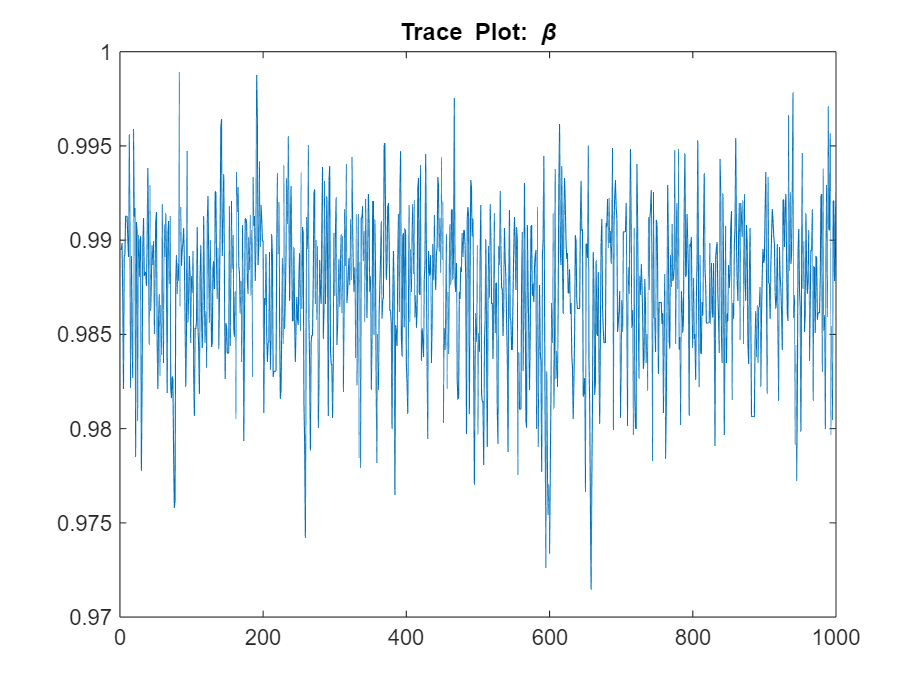

figure
plot(PosteriorMdl.ParamDistribution(2,:))
title("Trace Plot: \alpha")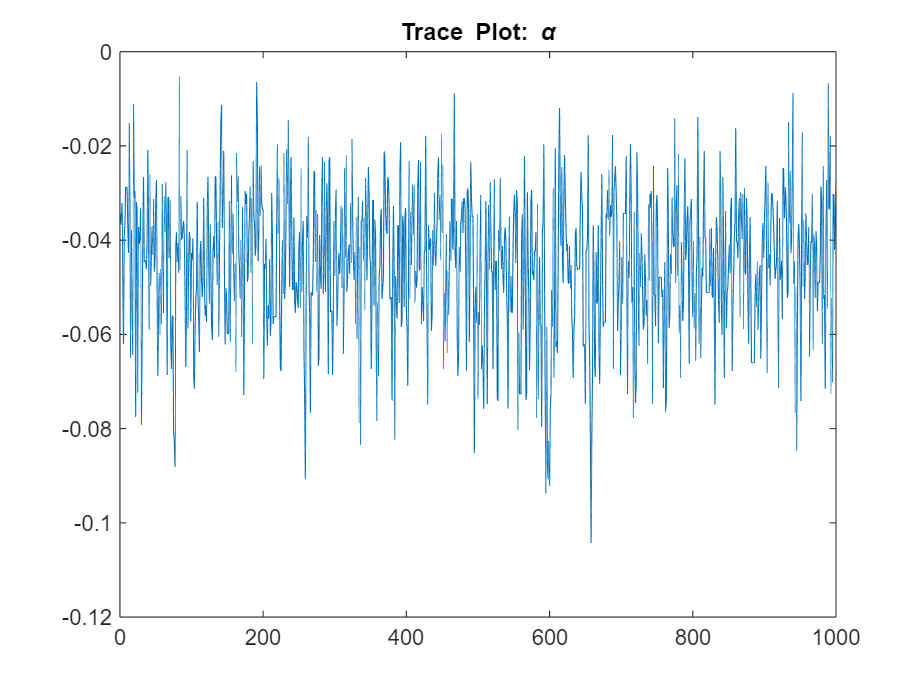

figure
plot(PosteriorMdl.ParamDistribution(3,:))
title("Trace Plot: \sigma")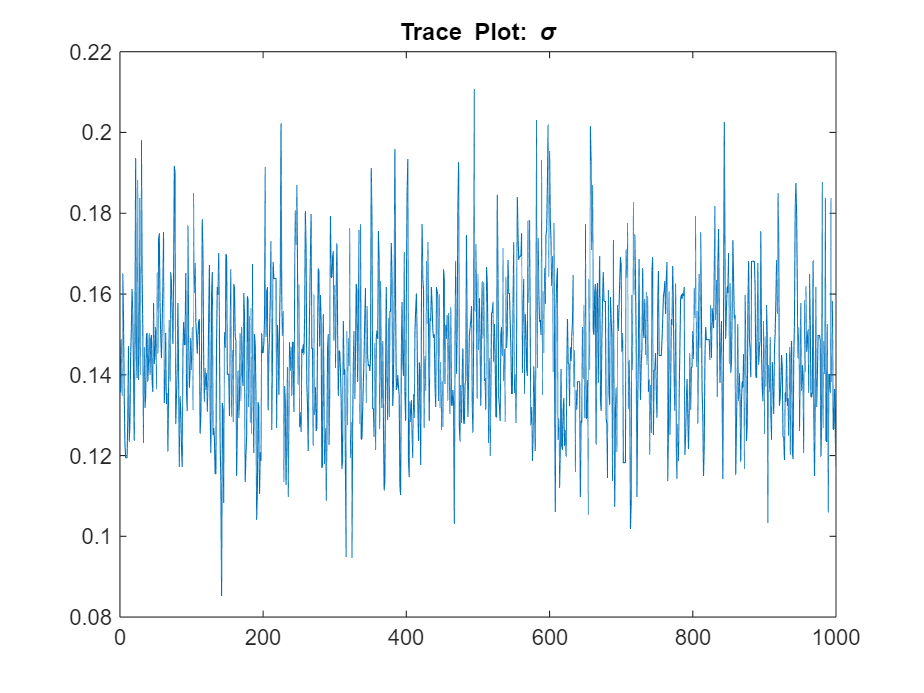

The posterior samples show good mixing with some minor serial correlation.

Local Functions

This example uses the following functions. paramMap is the parameter-to-matrix mapping function and flatLogPrior is the log prior distribution of the parameters.

function [A,B,LogY,Mean0,Cov0,StateType] = paramMap(theta)
    A = @(x) theta(2) + theta(1).*x;
    B = theta(3);
    LogY = @(y,x)-0.5.*x-0.5*365*y*y.*exp(-x);
    Mean0 = theta(2)./(1 - theta(1));          
    Cov0 = (theta(3)^2)./(1 - theta(1)^2);
    StateType = 0;
end

function logprior = flatLogPrior(theta)
% flatLogPrior computes the log of the flat prior density for the three
% variables in theta. Log probabilities for parameters outside the
% parameter space are -Inf.
    paramcon = zeros(numel(theta),1);
    % theta(1) is the lag 1 term in a stationary AR(1) model. The
    % value needs to be within the unit circle.
    paramcon(1) = abs(theta(1)) >= 1 - eps;

    % alpha must be finite
    paramcon(2) = ~isfinite(theta(2)); 

    % Standard deviation of the state disturbance theta(3) must be positive.
    paramcon(3) = theta(3) <= eps;

    if sum(paramcon) > 0
        logprior = -Inf;
    else
        logprior = 0;   % Prior density is proportional to 1 for all values
                        % in the parameter space.
    end
end

Input Arguments

collapse all

`PriorMdl` — Prior Bayesian nonlinear non-Gaussian state-space model
`bnlssm` model object

Prior Bayesian nonlinear non-Gaussian state-space model, specified as a bnlssm model object return by bnlssm.

The function handles of the properties PriorMdl.ParamDistribution and PriorMdl.ParamMap determine the prior and the data likelihood, respectively.

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

Observed response data, specified as a numeric matrix or a cell vector of numeric vectors.

If PriorMdl is time invariant with respect to the observation equation, Y is a T-by-n matrix. Each row of the matrix corresponds to a period and each column corresponds to a particular observation in the model. T is the sample size and n is the number of observations per period. The last row of Y contains the latest observations.
If PriorMdl is time varying with respect to the observation equation, Y is a T-by-1 cell vector. Y{t} contains an n_t-dimensional vector of observations for period t, where t = 1, ..., T. For linear observation models, the corresponding dimensions of the coefficient matrices, outputs of PriorMdl.ParamMap, C{t}, and D{t} must be consistent with the matrix in Y{t} for all periods. For nonlinear observation models, the dimensions of the inputs and outputs associated with the observations must be consistent. Regardless of model type, the last cell of Y contains the latest observations.

NaN elements indicate missing observations. For details on how estimate accommodates missing observations, see Algorithms.

Data Types: double | cell

`params0` — Initial values for parameters Θ
numeric vector

Initial parameter values for the parameters Θ, specified as a numParams-by-1 numeric vector. Elements of params0 must correspond to the elements of the first input arguments of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: estimate(PriorMdl,Y,params0,NumDraws=1e3,Thin=4,DoF=10) uses the multivariate t₁₀ distribution for the MH proposal, draws 4e3 random vectors of parameters, and thins the sample to reduce serial correlation by discarding every 3 draws until it retains 1e3 draws.

Posterior Sampling Options

collapse all

`NumDraws` — Number of MCMC sampler draws
`1000` (default) | positive integer

Number of MCMC sampler draws from the posterior distribution Π(θ|Y), specified as a positive integer.

Example: NumDraws=1e5

Data Types: double

`BurnIn` — Number of draws to remove from beginning of sample
`100` (default) | nonnegative scalar

Number of draws to remove from the beginning of the sample to reduce transient effects, specified as a nonnegative scalar. For details on how estimate reduces the full sample, see Algorithms.

Tip

To help you specify the appropriate burn-in period size:

Determine the extent of the transient behavior in the sample by setting the BurnIn name-value argument to 0.
Simulate a few thousand observations by using simulate.
Create trace plots.

Example: BurnIn=1000

Data Types: double

`Thin` — Adjusted sample size multiplier
`1` (no thinning) (default) | positive integer

Adjusted sample size multiplier, specified as a positive integer.

The actual sample size is BurnIn + NumDraws*Thin. After discarding the burn-in, estimate discards every Thin – 1 draws, and then retains the next draw. For more details on how estimate reduces the full sample, see Algorithms.

Tip

To reduce potential large serial correlation in the posterior sample, or to reduce the memory consumption of the output sample, specify a large value for Thin.

Example: Thin=5

Data Types: double

`DoF` — Proposal distribution degrees of freedom
`Inf` (default) | positive scalar

Proposal distribution degrees of freedom for parameter updates using the MH sampler, specified as a value in this table.

Value	MH Proposal Distribution
Positive scalar	Multivariate t with `DoF` degrees of freedom
`Inf`	Multivariate normal

The following options specify other aspects of the proposal distribution:

Proportion — Optional proportionality constant that scales Proposal
Center — Optional expected value

Example: DoF=10

Data Types: double

`Proportion` — Proposal scale matrix proportionality constant
`1` (default) | positive scalar

Proposal scale matrix proportionality constant, specified as a positive scalar.

Tip

For higher proposal acceptance rates, experiment with relatively small values for Proportion.

Example: Proportion=1

Data Types: double

`Center` — Proposal distribution center
`[]` (default) | numeric vector

Proposal distribution center, specified as a value in this table.

Value	Description
`numParams`-by-1 numeric vector	`estimate` uses the independence Metropolis-Hastings sampler. `Center` is the center of the proposal distribution.
`[]` (empty array)	`estimate` uses the random-walk Metropolis-Hastings sampler. The center of the proposal density is the current state of the Markov chain.

Example: Center=ones(10,1)

Data Types: double

`NumParticles` — Number of particles
`1000` (default) | positive integer

Number of particles for SMC, specified as a positive integer.

Example: NumParticles=1e4

Data Types: double

`NumPaths` — Number of sample state paths
`200` (default) | positive integer

Number of sample state paths to draw from the posterior smoothed state distribution, specified as a positive integer.

Example: NumPaths=1e4

Data Types: double

`Resample` — SMC resampling method
`"multinomial"` (default) | `"residual"` | `"systematic"`

SMC resampling method, specified as a value in this table.

Value	Description
`"multinomial"`	At time t, the set of previously generated particles (parent set) follows a standard multinomial distribution, with probabilities proportional to their weights. An offspring set is resampled with replacement from the parent set [1].
`"residual"`	Residual sampling, a modified version of multinomial resampling that can produce an estimator with lower variance than the multinomial resampling method [7].
`"systematic"`	Systematic sampling, which produces an estimator with lower variance than the multinomial resampling method [4].

Resampling methods downsample insignificant particles to achieve a smaller estimator variance than if no resampling is performed and to avoid sampling from a degenerate proposal [4].

Example: Resample="residual"

Data Types: char | string

`Cutoff` — Effective sample size threshold for resampling
`0.5*NumParticles` (default) | nonnegative scalar

Effective sample size threshold, below which estimate resamples particles, specified as a nonnegative scalar. For more details, see [4], Ch. 12.3.3.

Tip

To resample during every period, set Cutoff=numparticles, where numparticles is the value of the NumParticles name-value argument.
To avoid resampling, set Cutoff=0.

Example: Cutoff=0.75*numparticles

Data Types: double

`SortParticles` — Flag for sorting particles before resampling
`true` (default) | `false`

Flag for sorting particles before resampling, specified as a value in this table.

Value	Description
`true`	`estimate` sorts the generated particles before resampling them.
`false`	`estimate` does not sort the generated particles.

When SortPartiles=true, estimate uses Hilbert sorting during the SMC routine to sort the particles. This action can reduce Monte Carlo variation, which is useful when you compare loglikelihoods resulting from evaluating several params arguments that are close to each other [3]. However, the sorting routine requires more computation resources, and can slow down computations, particularly in problems with a high-dimensional state variable.

Example: SortParticles=false

Data Types: logical

`Autocorrelation` — Autocorrelation of normal random numbers
`0.99` (default) | positive scalar in [0,1]

Autocorrelation of normal random numbers for particle generation and resampling during SMC, specified as a positive scalar in the interval [0,1].

For 0, estimate randomly generates new numbers independently of those previously drawn.
For 1, estimate generates an initial set of random numbers, but uses those same numbers for the duration of SMC sampling.
For a value between 0 and 1, exclusive, estimate generates the random numbers of sample j, s_j, using $s_{j} = ϕ s_{j - 1} + z_{j} \sqrt{1 - ϕ^{2}}$ , where z_j is a set of iid standard normal variates.

Example: Autocorrelation=0.5

Data Types: double

Proposal Tuning Options

collapse all

`Lower` — Parameter lower bounds
`[]` (default) | numeric vector

Parameter lower bounds when computing the Hessian matrix (see Hessian), specified as a numParams-by-1 numeric vector.

Lower(j) specifies the lower bound of parameter theta(j), the first input argument of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

The default value [] specifies no lower bounds.

Note

Lower does not apply to posterior simulation. To apply parameter constraints on the posterior, code them in the log prior distribution function PriorMdl.ParamDistribution by setting the log prior of values outside the distribution support to -Inf.

Example: Lower=[0 -5 -1e7]

Data Types: double

`Upper` — Parameter upper bounds
`[]` (default) | numeric vector

Parameter lower bounds when computing the Hessian matrix (see Hessian), specified as a numParams-by-1 numeric vector.

Upper(j) specifies the upper bound of parameter theta(j), the first input argument of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

The default value [] specifies no upper bounds.

Note

Upper does not apply to posterior simulation. To apply parameter constraints on the posterior, code them in the log prior distribution function PriorMdl.ParamDistribution by setting the log prior of values outside the distribution support to -Inf.

Example: Upper=[5 100 1e7]

Data Types: double

`Options` — Optimization options
`optimoptions` optimization controller

Optimization options for tuning the proposal distribution, specified as an optimoptions optimization controller. Options replaces default optimization options of the optimizer. For details on altering default values of the optimizer, see the optimization controller optimoptions, the constrained optimization function fmincon, or the unconstrained optimization function fminunc in Optimization Toolbox™.

For example, to change the constraint tolerance to 1e-6, set options = optimoptions(@fmincon,ConstraintTolerance=1e-6,Algorithm="sqp"). Then, pass Options by using Options=options.

By default, estimate uses the default options of the optimizer.

`StepSizeFirstDerivative` — Step size for computing first derivatives
`1e-6` (default) | positive scalar

Step size for computing the first derivatives that comprise the Hessian matrix (see Hessian), specified as a positive scalar.

Example: StepSizeFirstDerivative=1e-4

Data Types: double

`StepSizeSecondDerivative` — Step size for computing second derivatives
`1e-4` (default) | positive scalar

Step size for computing the second derivatives that comprise the Hessian matrix (see Hessian), specified as a positive scalar.

Example: StepSizeSecondDerivative=1e-3

Data Types: double

`Hessian` — Hessian approximation method
`"difference"` (default) | `"diagonal"` | `"opg"` | character vector

Hessian approximation method for the MH proposal distribution scale matrix, specified as a value in this table.

Value	Description
`"difference"`	Finite differencing
`"diagonal"`	Diagonalized result of finite differencing
`"opg"`	Outer product of gradients, ignoring the prior distribution

Tip

The Hessian="difference" setting can be computationally intensive and inaccurate, and the resulting scale matrix can be nonnegative definite. Try one of the other options for better results.

Example: Hessian="opg"

Data Types: char | string

Other Options

collapse all

`Display` — Control for displaying proposal tuning and posterior simulation results
`"summary"` (default) | `"full"` | `"off"` | character vector

Control for displaying proposal tuning and posterior simulation results, specified as a value in this table.

Value	Description
`"off"`	Suppress all output.
`"summary"`	Display a summary of proposal tuning and posterior simulation results.
`"full"`	Display proposal tuning and posterior simulation details.

Example: Display="full"

Data Types: string | char

Output Arguments

collapse all

`PosteriorMdl` — Posterior Bayesian state-space model
`bnlssm` model object

Posterior Bayesian nonlinear non-Gaussian state-space model, returned as a bnlssm model object.

The property PosteriorMdl.ParamDistribution is a numParams-by-NumDraws sample from the posterior distribution of Θ|y. PosteriorMdl.ParamDistribution(j,:) contains a NumDraws sample of the parameter theta(j), where theta corresponds to Θ, and it is the first input argument of PriorMdl.ParamMap and PriorMdl.ParamDistribution.

The properties PosteriorMdl.ParaMap and PrioirMdl.ParamMap are equal.

`estParams` — Posterior means of Θ
numeric vector

Posterior means of Θ, returned as a numParams-by-1 numeric vector. estParams(j) contains the mean of the NumDraws posterior sample of the parameter theta(j).

`EstParamCov` — Variance-covariance matrix of estimates of Θ
numeric matrix

Variance-covariance matrix of estimates of Θ, returned as a numParams-by-numParams numeric matrix. EstParamCov(j,k) contains the estimated covariance of the parameter estimates of theta(j) and theta(k), based on the NumDraws posterior sample of those parameters.

`Summary` — Summary of all Bayesian estimators
structure array

Summary of all Bayesian estimators, returned as a table.

Rows of the table correspond to elements of Θ, final state values, and estimated state disturbance and observation innovation hyperparameters:

For the first numParams rows of the table, row j contains the posterior estimation summary of theta(j).
If the distribution of the state disturbances or observation innovations is non-Gaussian, the following statements hold:
- Rows numParams + k contains the posterior estimation summary of the final value of state k.

Columns contain the posterior mean Mean, standard deviation Std, 5% percentile Quantile05, and 95% percentile Quantile95.

Tips

Unless you set Cutoff=0, estimate resamples particles according to the specified resampling method Resample. Although resampling particles with high weights improves the results of the SMC, you should also allow the sampler traverse the proposal distribution to obtain novel, high-weight particles. To do this, experiment with Cutoff.
Avoid an arbitrary choice of the initial state distribution. bnlssm functions generate the initial particles from the specified initial state distribution, which impacts the performance of the nonlinear filter. If the initial state specification is bad enough, importance weights concentrate on a small number of particles in the first SMC iteration, which might produce unreasonable filtering results. This vulnerability of the nonlinear model behavior contrasts with the stability of the Kalman filter for the linear model, in which the initial state distribution usually has little impact on the filter because the prior is washed out as it processes data.

Algorithms

estimate accommodates missing data by not updating filtered state estimates corresponding to missing observations. In other words, suppose there is a missing observation at period t. Then, the state forecast for period t based on the previous t – 1 observations and filtered state for period t are equivalent.
estimate uses the tune function to create the proposal distribution for the MH sampler. You can tune the sampler by using the proposal tuning options.
When estimate tunes the proposal distribution, the optimizer that estimate uses to search for the posterior mode before computing the Hessian matrix depends on your specifications.
- estimate uses fminunc by default.
- estimate uses fmincon when you perform constrained optimization by specifying the Lower or Upper name-value argument.
This figure shows how estimate reduces the sample by using the values of NumDraws, Thin, and BurnIn. Rectangles represent successive draws from the distribution. estimate removes the white rectangles from the sample. The remaining NumDraws black rectangles compose the sample.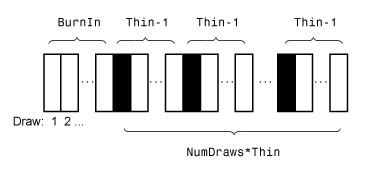

References

[1] Andrieu, Christophe, Arnaud Doucet, and Roman Holenstein. "Particle Markov Chain Monte Carlo Methods." Journal of the Royal Statistical Society Series B: Statistical Methodology 72 (June 2010): 269–342. https://doi.org/10.1111/j.1467-9868.2009.00736.x.

[2] Andrieu, Christophe, and Gareth O. Roberts. "The Pseudo-Marginal Approach for Efficient Monte Carlo Computations." Ann. Statist. 37 (April 2009): 697–725. https://dx.doi.org/10.1214/07-AOS574.

[3] Deligiannidis, George, Arnaud Doucet, and Michael Pitt. "The Correlated Pseudo-Marginal Method." Journal of the Royal Statistical Society, Series B: Statistical Methodology 80 (June 2018): 839–870. https://doi.org/10.1111/rssb.12280.

[4] Durbin, J, and Siem Jan Koopman. Time Series Analysis by State Space Methods. 2nd ed. Oxford: Oxford University Press, 2012.

[5] Fernández-Villaverde, Jesús, and Juan F. Rubio-Ramírez. "Estimating Macroeconomic Models: A Likelihood Approach." Review of Economic Studies 70(October 2007): 1059–1087. https://doi.org/10.1111/j.1467-937X.2007.00437.x.

[6] Hastings, Wilfred K. "Monte Carlo Sampling Methods Using Markov Chains and Their Applications." Biometrika 57 (April 1970): 97–109. https://doi.org/10.1093/biomet/57.1.97.

[7] Liu, Jun, and Rong Chen. "Sequential Monte Carlo Methods for Dynamic Systems." Journal of the American Statistical Association 93 (September 1998): 1032–1044. https://dx.doi.org/10.1080/01621459.1998.10473765.

[8] Metropolis, Nicholas, Rosenbluth, Arianna. W., Rosenbluth, Marshall. N., Teller, Augusta. H., and Teller, Edward. "Equation of State Calculations by Fast Computing Machines." The Journal of Chemical Physics 21 (June 1953): 1087–92. https://doi.org/10.1063/1.1699114.

Version History

Introduced in R2024b

estimate

Syntax

Description

Examples

Estimate Posterior Distribution

Improve Markov Chain Convergence

Return Posterior Moments and Inferences

Estimate Posterior of Stochastic Volatility Model

Input Arguments

PriorMdl — Prior Bayesian nonlinear non-Gaussian state-space model bnlssm model object

Y — Observed response data numeric matrix | cell vector of numeric vectors

params0 — Initial values for parameters Θ numeric vector

Name-Value Arguments

NumDraws — Number of MCMC sampler draws 1000 (default) | positive integer

BurnIn — Number of draws to remove from beginning of sample 100 (default) | nonnegative scalar

Thin — Adjusted sample size multiplier 1 (no thinning) (default) | positive integer

DoF — Proposal distribution degrees of freedom Inf (default) | positive scalar

Proportion — Proposal scale matrix proportionality constant 1 (default) | positive scalar

Center — Proposal distribution center [] (default) | numeric vector

NumParticles — Number of particles 1000 (default) | positive integer

NumPaths — Number of sample state paths 200 (default) | positive integer

Resample — SMC resampling method "multinomial" (default) | "residual" | "systematic"

Cutoff — Effective sample size threshold for resampling 0.5*NumParticles (default) | nonnegative scalar

SortParticles — Flag for sorting particles before resampling true (default) | false

Autocorrelation — Autocorrelation of normal random numbers 0.99 (default) | positive scalar in [0,1]

Lower — Parameter lower bounds [] (default) | numeric vector

Upper — Parameter upper bounds [] (default) | numeric vector

Options — Optimization options optimoptions optimization controller

StepSizeFirstDerivative — Step size for computing first derivatives 1e-6 (default) | positive scalar

StepSizeSecondDerivative — Step size for computing second derivatives 1e-4 (default) | positive scalar

Hessian — Hessian approximation method "difference" (default) | "diagonal" | "opg" | character vector

Display — Control for displaying proposal tuning and posterior simulation results "summary" (default) | "full" | "off" | character vector

Output Arguments

PosteriorMdl — Posterior Bayesian state-space model bnlssm model object

estParams — Posterior means of Θ numeric vector

EstParamCov — Variance-covariance matrix of estimates of Θ numeric matrix

Summary — Summary of all Bayesian estimators structure array

Tips

Algorithms

References

Version History

See Also

Objects

Functions

`PriorMdl` — Prior Bayesian nonlinear non-Gaussian state-space model
`bnlssm` model object

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

`params0` — Initial values for parameters Θ
numeric vector

`NumDraws` — Number of MCMC sampler draws
`1000` (default) | positive integer

`BurnIn` — Number of draws to remove from beginning of sample
`100` (default) | nonnegative scalar

`Thin` — Adjusted sample size multiplier
`1` (no thinning) (default) | positive integer

`DoF` — Proposal distribution degrees of freedom
`Inf` (default) | positive scalar

`Proportion` — Proposal scale matrix proportionality constant
`1` (default) | positive scalar

`Center` — Proposal distribution center
`[]` (default) | numeric vector

`NumParticles` — Number of particles
`1000` (default) | positive integer

`NumPaths` — Number of sample state paths
`200` (default) | positive integer

`Resample` — SMC resampling method
`"multinomial"` (default) | `"residual"` | `"systematic"`

`Cutoff` — Effective sample size threshold for resampling
`0.5*NumParticles` (default) | nonnegative scalar

`SortParticles` — Flag for sorting particles before resampling
`true` (default) | `false`

`Autocorrelation` — Autocorrelation of normal random numbers
`0.99` (default) | positive scalar in [0,1]

`Lower` — Parameter lower bounds
`[]` (default) | numeric vector

`Upper` — Parameter upper bounds
`[]` (default) | numeric vector

`Options` — Optimization options
`optimoptions` optimization controller

`StepSizeFirstDerivative` — Step size for computing first derivatives
`1e-6` (default) | positive scalar

`StepSizeSecondDerivative` — Step size for computing second derivatives
`1e-4` (default) | positive scalar

`Hessian` — Hessian approximation method
`"difference"` (default) | `"diagonal"` | `"opg"` | character vector

`Display` — Control for displaying proposal tuning and posterior simulation results
`"summary"` (default) | `"full"` | `"off"` | character vector

`PosteriorMdl` — Posterior Bayesian state-space model
`bnlssm` model object

`estParams` — Posterior means of Θ
numeric vector

`EstParamCov` — Variance-covariance matrix of estimates of Θ
numeric matrix

`Summary` — Summary of all Bayesian estimators
structure array