imfindcircles

使用圆形霍夫变换查找圆

全页折叠

语法

centers = imfindcircles(A,radius)

[centers,radii] = imfindcircles(A,radiusRange)

[centers,radii,metric] = imfindcircles(A,radiusRange)

[___] = imfindcircles(___,Name=Value)

说明

centers = imfindcircles(A,radius) 查找图像 A 中半径约等于 radius 的圆。输出 centers 是一个两列矩阵，其中包含图像中各圆中心的 (x,y) 坐标。

[centers,radii] = imfindcircles(A,radiusRange) 查找半径在 radiusRange 指定范围内的圆。附加输出参量 radii 包含与 centers 中每个圆心对应的估计半径。

[centers,radii,metric] = imfindcircles(A,radiusRange) 还返回列向量 metric，其中包含每个圆的累加器数组峰值的幅值（按降序排列）。centers 和 radii 的行对应于 metric 的行。

示例

[___] = imfindcircles(___,Name=Value) 支持任何上述语法，且可使用一个或多个名称-值参量指定其他选项。

示例

全部折叠

检测图像中的五个强度最大的圆形

打开实时脚本

此示例说明如何找到一个图像中的所有圆形，以及如何保留和显示强度最大的圆形。

将灰度图像读入工作区并显示它。

A = imread('coins.png');
imshow(A)

Figure contains an axes object. The hidden axes object contains an object of type image.

查找半径为 r 个像素且在 [15, 30] 范围内的所有圆形。

[centers, radii, metric] = imfindcircles(A,[15 30]);

根据度量值保留五个强度最大的圆形。

centersStrong5 = centers(1:5,:); 
radiiStrong5 = radii(1:5);
metricStrong5 = metric(1:5);

在原始图像上绘制五个强度最大的圆周。

viscircles(centersStrong5, radiiStrong5,'EdgeColor','b');

Figure contains an axes object. The hidden axes object contains 3 objects of type line, image.

在图像中的亮圆和暗圆周围绘制线条

打开实时脚本

将图像读入工作区中并显示它。

A = imread('circlesBrightDark.png');
imshow(A)

Figure contains an axes object. The hidden axes object contains an object of type image.

定义半径范围。

Rmin = 30;
Rmax = 65;

找出图像中半径范围内的所有亮圆。

[centersBright, radiiBright] = imfindcircles(A,[Rmin Rmax],'ObjectPolarity','bright');

找出图像中半径范围内的所有暗圆。

[centersDark, radiiDark] = imfindcircles(A,[Rmin Rmax],'ObjectPolarity','dark');

在亮圆的边缘周围绘制蓝色线条。

viscircles(centersBright, radiiBright,'Color','b');

Figure contains an axes object. The hidden axes object contains 3 objects of type line, image.

在暗圆的边缘周围绘制红色虚线。

viscircles(centersDark, radiiDark,'LineStyle','--');

Figure contains an axes object. The hidden axes object contains 5 objects of type line, image.

输入参数

全部折叠

`A` — 输入图像
灰度图像 | 真彩色图像 | 二值图像

输入图像是在其中检测圆形目标的图像，指定为灰度图像、真彩色 (RGB) 图像或二值图像。

`radius` — 圆半径
正数

圆半径活要检测的圆形目标的近似半径，指定为正数。

`radiusRange` — 半径范围
由正整数组成的二元素向量

要检测的圆形目标的半径范围，指定为 [rmin rmax] 形式的由正整数组成的二元素向量，其中 rmin 小于 rmax。

名称-值参数

全部折叠

将可选参量对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

示例: centers = imfindcircles(A,radius,ObjectPolarity=bright) 在深色背景上指定亮色圆形目标。

如果使用的是 R2021a 之前的版本，请使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: centers = imfindcircles(A,radius,"ObjectPolarity","bright") 在深色背景上指定亮色圆形目标。

`ObjectPolarity` — 目标极性
`"bright"` (默认) | `"dark"`

目标极性，指定为下表中的值之一。

`"bright"`	圆形目标比背景亮。
`"dark"`	圆形目标比背景暗。

`Method` — 计算方法
`"PhaseCode"` (默认) | `"TwoStage"`

用于计算累加器数组的计算方法，指定为下表中的值之一。

`"PhaseCode"`	Atherton 和 Kerbyson 的 [1] 相位编码方法。
`"TwoStage"`	两阶段圆形霍夫变换 [2]、[3] 中使用的方法。

`Sensitivity` — 敏感度因子
`0.85` (默认) | [0, 1] 范围内的数值

圆形霍夫变换累加器数组的敏感度因子，指定为范围 [0, 1] 内的数值。随着敏感度因子的增大，imfindcircles 会检测到更多圆形目标，包括弱圆形和部分模糊圆形。更高的敏感度值也会增加错误检测的风险。

`EdgeThreshold` — 边缘梯度阈值
[0, 1] 范围内的数值

用于确定图像中边缘像素的边缘梯度阈值，指定为范围 [0, 1] 内的数字。指定 0 可将阈值设置为零梯度幅值。指定 1 可将阈值设置为最大梯度幅值。阈值设置得越低，imfindcircles 检测到的圆形目标（具有弱边缘和强边缘）越多。随着阈值的增大，它会检测到较少的具有弱边缘的圆形。默认情况下，imfindcircles 使用函数 graythresh 自动选择边缘梯度阈值。

输出参量

全部折叠

`centers` — 圆心坐标
P×`2` 矩阵

圆心坐标，返回为 P×2 矩阵，第一列中包含圆心的 x 坐标，第二列中包含 y 坐标。行数 P 是检测到的圆形的个数。centers 根据圆形的强度（从最强到最弱）排序。

数据类型: double

`radii` — 估计半径
列向量

各圆心对应的估计半径，以列向量形式返回。radii(j) 处的半径值对应于以 centers(j,:) 为中心的圆形。

数据类型: double

`metric` — 圆形的强度
列向量

圆形的强度提供各圆心的相对强度，以列向量形式返回。metric(j) 处的值对应于以 centers(j,:) 为中心、半径为 radii(j) 的圆。

数据类型: double

提示

当 radius（或 rmin）的值小于或等于 5 时，imfindcircles 的准确度会受到限制。
如果使用 "PhaseCode" 方法（默认值）而不是 "TwoStage"，半径估计步骤通常会更快。
"PhaseCode" 和 "TwoStage" 这两种计算方法检测同心圆的能力有限。同心圆的结果可能因输入图像而异。
imfindcircles 找不到圆心位于图像区域之外的圆形。
对于真彩色图像，imfindcircles 在处理之前会先用 rgb2gray 函数将图像转换为灰度图像。对于二值 (logical) 图像和整数类型图像，在处理之前会用 im2single 函数转换为 single 数据类型。为了提高二值图像结果的准确度，imfindcircles 还使用 imfilter 作为预处理步骤来应用高斯平滑。

算法

imfindcircles 使用基于圆形霍夫变换 (CHT) 的算法在图像中寻找圆形。之所以使用这种方法，是因为当存在噪声、遮挡和变化的光照条件时该方法表现稳健。

CHT 并非严格指定的算法，在其实现中可采用许多不同方法。然而，有三个重要步骤是所有方法共有的。

累加器数组计算
高梯度的前景像素指定为候选像素，并允许在累加器数组中“投票”。在经典 CHT 实现中，候选像素在围绕像素构成一个固定半径全圆的模式中投票。在图 1a 所示的示例中显示了一个实际圆（实线圆）上的候选像素以及该候选像素的经典 CHT 投票模式（虚线圆）。
经典 CHT 投票模式
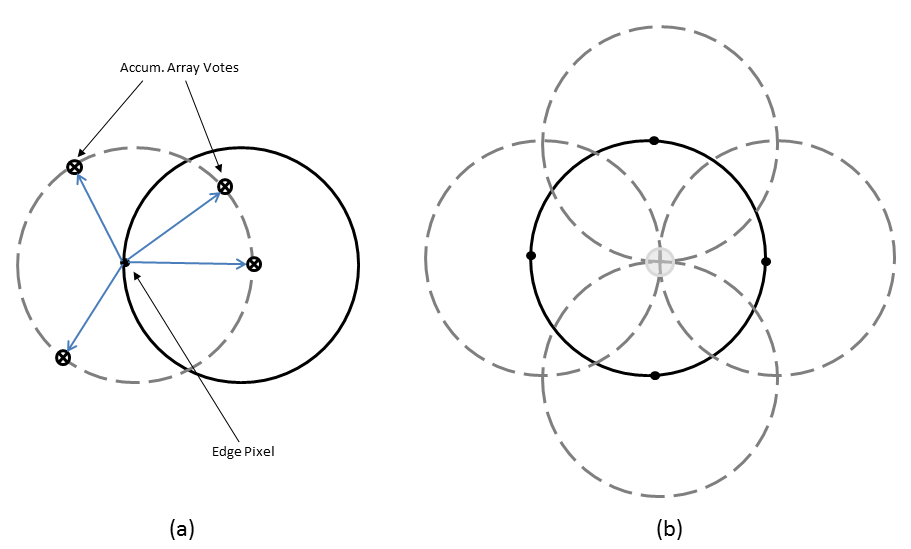
中心估计
属于同一个图像圆的各候选像素的投票趋于在对应于该圆中心的累加器数组 bin 中累加。因此，可通过检测累加器数组中的峰值来估计圆心。在图 1b 所示的示例中显示一个实际圆（实线圆）上的各候选像素（实心点）以及它们的投票模式（虚线圆），这些模式在实际圆的中心处重合。
半径估计
如果同一累加器数组用于多个半径值（这是 CHT 算法中的常见做法），则必须以单独的步骤来估计检测到的圆的半径。

imfindcircles 提供两种在图像中寻找圆的算法：相位编码（默认值）和两阶段算法。两者有一些共同的计算步骤，但也各有特色。

这两种算法共有的计算功能如下：

二维累加器数组的使用
经典霍夫变换需要三维数组来存储多个半径的投票，这需要很大的存储空间和很长的处理时间。相位编码方法和两阶段方法都通过对所有半径使用同一个二维累加器数组来解决此问题。虽然这样做需要额外的半径估计步骤，但总体计算负载通常较低，尤其是在处理大半径范围时。这是目前 CHT 实现中广泛采用的做法。
边缘像素的使用
整体内存要求和速度很大程度上取决于候选像素的数量。为了限制其数量，请为输入图像的梯度幅值设置阈值，以便在计票中只包括高梯度的像素。
边缘方向信息的使用
通过限制候选像素可用的 bin 的数量，也可以优化性能。这是通过使用局部可用的边缘信息来实现的，它只允许在沿梯度方向的有限区间内投票（图 2）。图中点 c_min 和 c_max 之间的投票区间的宽度由 r_min 和 r_max 定义的半径范围确定。
投票模式：多个半径，沿梯度方向

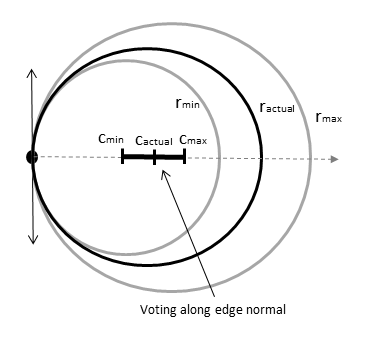
r_min	最小搜索半径
r_max	最大搜索半径
r_actual	候选像素所属的圆的半径
c_min	半径为 r_min 的圆心
c_max	半径为 r_max 的圆心
c_actual	半径为 r_actual 的圆心

函数 imfindcircles 使用的两种 CHT 方法在计算圆半径的方式上有根本的不同。

两阶段
使用估计的圆心和图像信息显式估计半径。该方法基于计算径向直方图 [2] [3]。
相位编码
半径是根据累加器数组中的复数值估算的，在数组项的相位中对半径信息进行编码[1]。边缘像素所投的票不仅包含关于可能的中心位置的信息，还包含关于与中心位置相关联的圆的半径的信息。与必须使用径向直方图显式估计半径的两阶段方法不同，在相位编码方法中，可通过简单地解码来自累加器数组中估计的中心位置的相位信息来估计半径。

参考

[1] T.J Atherton, D.J. Kerbyson. "Size invariant circle detection." Image and Vision Computing. Volume 17, Number 11, 1999, pp. 795-803.

[2] H.K Yuen, J. Princen, J. Illingworth, and J. Kittler. "Comparative study of Hough transform methods for circle finding." Image and Vision Computing. Volume 8, Number 1, 1990, pp. 71–77.

[3] E.R. Davies, Machine Vision: Theory, Algorithms, Practicalities. Chapter 10. 3rd Edition. Morgan Kauffman Publishers, 2005.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

imfindcircles 支持 C 代码生成（需要 MATLAB^® Coder™）。请注意，如果您选择通用的 MATLAB Host Computer 目标平台，imfindcircles 生成的代码将使用平台特定的预编译共享库。使用共享库可保留性能上的优化，但适用范围仅限于生成的代码所适用的目标平台。有关详细信息，请参阅Image Processing Toolbox 中代码生成支持的类型。
生成代码时，所有字符向量输入参数和值都必须为编译时常量。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

用法说明和限制：

当敏感度因子接近或等于 1 时，生成代码和 MATLAB 仿真的结果之间可能存在微小的不匹配。

版本历史记录

在 R2012a 中推出

全部展开

R2022a: 使用 GPU Coder 生成 CUDA 代码

imfindcircles 现在支持生成优化的 CUDA^® 代码（需要 GPU Coder™）。

R2019a: 对逻辑图像使用新滤波器大小

从 R2019a 开始，imfindcircles 函数使用 5×5 滤波器大小对逻辑图像进行平滑处理。imfindcircles 现在可能会返回与以前版本不同的结果，以前版本使用的滤波器大小为 6×6。例如，在某些情况下，该函数可能返回不同数量的圆。

另请参阅

circles2mask | hough | houghpeaks | houghlines | viscircles

主题

检测和测量图像中的圆形目标

imfindcircles

语法

说明

示例

检测图像中的五个强度最大的圆形

在图像中的亮圆和暗圆周围绘制线条

输入参数

A — 输入图像 灰度图像 | 真彩色图像 | 二值图像

radius — 圆半径 正数

radiusRange — 半径范围 由正整数组成的二元素向量

名称-值参数

ObjectPolarity — 目标极性 "bright" (默认) | "dark"

Method — 计算方法 "PhaseCode" (默认) | "TwoStage"

Sensitivity — 敏感度因子 0.85 (默认) | [0, 1] 范围内的数值

EdgeThreshold — 边缘梯度阈值 [0, 1] 范围内的数值

输出参量

centers — 圆心坐标 P×2 矩阵

radii — 估计半径 列向量

metric — 圆形的强度 列向量

提示

算法

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成 使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

版本历史记录

R2022a: 使用 GPU Coder 生成 CUDA 代码

R2019a: 对逻辑图像使用新滤波器大小

另请参阅

主题

`A` — 输入图像
灰度图像 | 真彩色图像 | 二值图像

`radius` — 圆半径
正数

`radiusRange` — 半径范围
由正整数组成的二元素向量

`ObjectPolarity` — 目标极性
`"bright"` (默认) | `"dark"`

`Method` — 计算方法
`"PhaseCode"` (默认) | `"TwoStage"`

`Sensitivity` — 敏感度因子
`0.85` (默认) | [0, 1] 范围内的数值

`EdgeThreshold` — 边缘梯度阈值
[0, 1] 范围内的数值

`centers` — 圆心坐标
P×`2` 矩阵

`radii` — 估计半径
列向量

`metric` — 圆形的强度
列向量

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。