标量函数的根
对一元非线性方程求解
fzero 函数尝试求一个一元方程的根。可以通过用于指定起始区间的单元素起点或双元素向量调用该函数。如果为 fzero 提供起点 x0,fzero 将首先搜索函数更改符号的点周围的区间。如果找到该区间,fzero 返回函数更改符号的位置附近的值。如果未找到此类区间,fzero 返回 NaN。或者,如果知道函数值的符号不同的两个点,可以使用双元素向量指定该起始区间;fzero 保证缩小该区间并返回符号更改处附近的值。
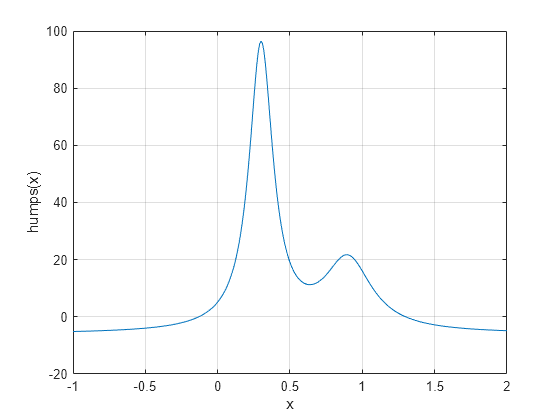
以下部分包含两个示例,用于说明如何使用起始区间和起点查找函数的零元素。这些示例使用由 MATLAB® 提供的函数 humps.m。下图显示了 humps 的图。
x = -1:.01:2; y = humps(x); plot(x,y) xlabel('x'); ylabel('humps(x)') grid on
为 fzero 设置选项
可以通过设置选项控制 fzero 函数的多个方面。使用 optimset 设置选项。选项包括:
使用起始区间
humps 的图指示 x = -1 时函数为负数,x = 1 时函数为正数。可以通过计算这两点的 humps 进行确认。
humps(1)
ans = 16
humps(-1)
ans = -5.1378
因此,可以将 [-1 1] 用作 fzero 的起始区间。
fzero 的迭代算法可求 [-1 1] 越来越小的子区间。对于每个子区间,humps 在两个端点的符号不同。由于子区间的端点彼此越来越近,因此它们收敛到 humps 的零位置。
要显示 fzero 在每个迭代过程中的进度,请使用 optimset 函数将 Display 选项设置为 iter。
options = optimset('Display','iter');
然后如下所示调用 fzero:
a = fzero(@humps,[-1 1],options)
Func-count x f(x) Procedure
2 -1 -5.13779 initial
3 -0.513876 -4.02235 interpolation
4 -0.513876 -4.02235 bisection
5 -0.473635 -3.83767 interpolation
6 -0.115287 0.414441 bisection
7 -0.115287 0.414441 interpolation
8 -0.132562 -0.0226907 interpolation
9 -0.131666 -0.0011492 interpolation
10 -0.131618 1.88371e-07 interpolation
11 -0.131618 -2.7935e-11 interpolation
12 -0.131618 8.88178e-16 interpolation
13 -0.131618 8.88178e-16 interpolation
Zero found in the interval [-1, 1]
a = -0.1316
每个值 x 代表迄今为止最佳的端点。Procedure 列向您显示每步的算法是使用对分还是插值。
可以通过输入以下内容验证 a 中的函数值是否接近零:
humps(a)
ans = 8.8818e-16
起点的使用
假定您不知道 humps 的函数值符号不同的两点。在这种情况下,可以选择标量 x0 作为 fzero 的起点。fzero 先搜索函数更改符号的点附近的区间。如果 fzero 找到此类区间,它会继续执行上一部分中介绍的算法。如果未找到此类区间,fzero 返回 NaN。
例如,将起点设置为 -0.2,将 Display 选项设置为 Iter,并调用 fzero:
options = optimset('Display','iter'); a = fzero(@humps,-0.2,options)
Search for an interval around -0.2 containing a sign change:
Func-count a f(a) b f(b) Procedure
1 -0.2 -1.35385 -0.2 -1.35385 initial interval
3 -0.194343 -1.26077 -0.205657 -1.44411 search
5 -0.192 -1.22137 -0.208 -1.4807 search
7 -0.188686 -1.16477 -0.211314 -1.53167 search
9 -0.184 -1.08293 -0.216 -1.60224 search
11 -0.177373 -0.963455 -0.222627 -1.69911 search
13 -0.168 -0.786636 -0.232 -1.83055 search
15 -0.154745 -0.51962 -0.245255 -2.00602 search
17 -0.136 -0.104165 -0.264 -2.23521 search
18 -0.10949 0.572246 -0.264 -2.23521 search
Search for a zero in the interval [-0.10949, -0.264]:
Func-count x f(x) Procedure
18 -0.10949 0.572246 initial
19 -0.140984 -0.219277 interpolation
20 -0.132259 -0.0154224 interpolation
21 -0.131617 3.40729e-05 interpolation
22 -0.131618 -6.79505e-08 interpolation
23 -0.131618 -2.98428e-13 interpolation
24 -0.131618 8.88178e-16 interpolation
25 -0.131618 8.88178e-16 interpolation
Zero found in the interval [-0.10949, -0.264]
a = -0.1316
每个迭代中当前子区间的端点列在标题 a 和 b 下,而端点处的相应 humps 值分别列在 f(a) 和 f(b) 下。
注意:端点 a 和 b 未按任何特定顺序列出:a 可能大于 b 或小于 b。
对于前 9 步,humps 的符号在当前子区间的两端点都为负号,如输出中所示。在第 10 步,humps 的符号在 a (-0.10949) 处为正号,但在 b (-0.264) 处为负号。从该点开始,如上一部分中所述,算法继续缩小区间 [-0.10949 -0.264],直到它达到值 -0.1316。