多项式的根
此示例演示如何通过多种不同的方法计算多项式的根。
数值根
roots 函数用于计算系数向量表示的单变量多项式的根。
例如,创建一个向量以表示多项式 ,然后计算多项式的根。
p = [1 -1 -6]; r = roots(p)
r =
3
-2按照惯例,MATLAB® 以列向量形式返回这些根。
poly 函数将这些根重新转换为多项式系数。对向量执行运算时,poly 和 roots 为逆函数,因此 poly(roots(p)) 返回 p(取决于舍入误差、排序和缩放)。
p2 = poly(r)
p2 =
1 -1 -6对矩阵执行运算时,poly 函数会计算矩阵的特征多项式。特征多项式的根是矩阵的特征值。因此,roots(poly(A)) 和 eig(A) 返回相同的答案(取决于舍入误差、排序和缩放)。
使用代换法求根
您可以通过使用代换法简化方程来对涉及三角函数的多项式方程求解。一个变量的生成多项式不再包含任何三角函数。
例如,计算 用于对该方程进行求解的值
利用 ,完全以正弦函数的方式表示该方程:
利用代换法 ,将该方程表示为简单的多项式方程:
创建一个向量以表示多项式。
p = [-3 -1 6];
求多项式的根。
r = roots(p)
r = 2×1
-1.5907
1.2573
要撤消代换法,请使用 。asin 函数计算反正弦。
theta = asin(r)
theta = 2×1 complex
-1.5708 + 1.0395i
1.5708 - 0.7028i
验证 theta 中的元素是否为 中用来对原始方程求解的值(在舍入误差内)。
f = @(Z) 3*cos(Z).^2 - sin(Z) + 3; f(theta)
ans = 2×1 complex
10-14 ×
-0.0888 + 0.0647i
0.2665 + 0.0399i
特定区间内的根
使用 fzero 函数求多项式在特定区间内的根。在其他使用情况下,如果您绘制多项式并想要知道特定根的值,则这种方法很适用。
例如,创建一个函数句柄以表示多项式 。
p = @(x) 3*x.^7 + 4*x.^6 + 2*x.^5 + 4*x.^4 + x.^3 + 5*x.^2;
在区间 内绘制该函数。
x = -2:0.1:1; plot(x,p(x)) ylim([-100 50]) grid on hold on
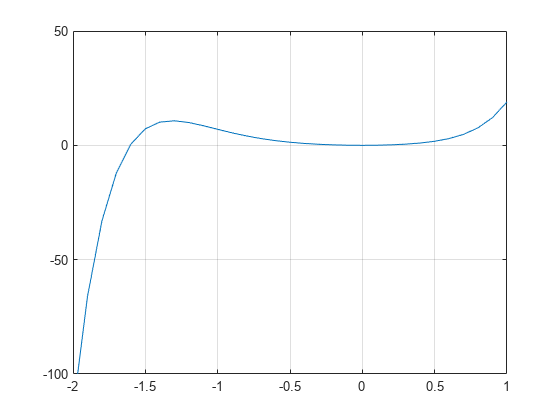
从绘图中,多项式在 0 和另一个接近 -1.5 的位置各有一个简单的根。使用 fzero 计算并绘制接近 -1.5 的根。
Z = fzero(p, -1.5)
Z = -1.6056
plot(Z,p(Z),'r*')
符号根
如果您有 Symbolic Math Toolbox™,则还会提供以符号形式计算多项式的其他选项。一种方式是使用 solve (Symbolic Math Toolbox) 函数。
syms x
s = solve(x^2-x-6)
s = -2 3
另一种方式是使用 factor (Symbolic Math Toolbox) 函数计算多项式各项的因子。
F = factor(x^2-x-6)
F = [ x + 2, x - 3]
有关详细信息,请参阅Solve Algebraic Equations (Symbolic Math Toolbox)。