cart2sph

将笛卡尔坐标转换为球面坐标

全页折叠

语法

[azimuth,elevation,r] = cart2sph(x,y,z)

说明

[azimuth,elevation,r] = cart2sph(x,y,z) 将笛卡尔坐标数组 x、y 和 z 的对应元素转换为球面坐标 azimuth、elevation 和 r。

示例

示例

全部折叠

打开实时脚本

将矩阵 x、y 和 z 中对应项定义的笛卡尔坐标转换为球面坐标 az、el 和 r。这些点对应于立方体的八个顶点。

x = [1 1 1 1; -1 -1 -1 -1]
x = 2×4

     1     1     1     1
    -1    -1    -1    -1


y = [1 1 -1 -1; 1 1 -1 -1]
y = 2×4

     1     1    -1    -1
     1     1    -1    -1


z = [1 -1 1 -1; 1 -1 1 -1]
z = 2×4

     1    -1     1    -1
     1    -1     1    -1


[az,el,r] = cart2sph(x,y,z)
az = 2×4

    0.7854    0.7854   -0.7854   -0.7854
    2.3562    2.3562   -2.3562   -2.3562


el = 2×4

    0.6155   -0.6155    0.6155   -0.6155
    0.6155   -0.6155    0.6155   -0.6155


r = 2×4

    1.7321    1.7321    1.7321    1.7321
    1.7321    1.7321    1.7321    1.7321

输入参数

全部折叠

笛卡尔坐标，指定为标量、向量、矩阵或多维数组。x、y 和 z 必须具有相同的大小或具有兼容的大小（例如，x 是一个 M×N 矩阵，y 以标量，z 是标量或 1×N 行向量）。有关详细信息，请参阅基本运算的兼容数组大小。

数据类型: single | double

输出参量

全部折叠

方位角，以数组形式返回。azimuth 是从 x 轴的正向测量的在 x-y 平面中的逆时针角度，以弧度为单位。角度值在 [-pi pi] 范围内。

仰角，以数组形式返回。elevation 是与 x-y 平面之间形成的仰角，以弧度为单位。角度值在 [-pi/2, pi/2] 范围内。

半径，以数组形式返回。r 是从原点到某点的距离。r 的长度单位可以是与输入数组 x、y 和 z 的单位匹配的任意单位。

算法

从三维笛卡尔坐标到球面坐标的映射为

azimuth = atan2(y,x)
elevation = atan2(z,sqrt(x.^2 + y.^2))
r = sqrt(x.^2 + y.^2 + z.^2)

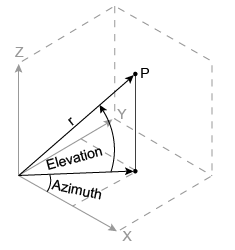
Figure shows a point plotted in 3-D space with X and Y in the horizontal plane and Z along the vertical axis. The point has a radius measured from the origin, an azimuthal angle measured in relation to X in the horizontal plane, and an elevation angle measured as elevation above the XY plane.

球面坐标表示法不是标准表示法。对于 cart2sph 函数而言，elevation 是从 x-y 平面进行测量的。请注意，如果 elevation = 0，则该点位于 x-y 平面中。如果 elevation = pi/2，则该点位于正 z 轴上。

扩展功能

全部展开

版本历史记录

在 R2006a 之前推出

另请参阅

| |