qz

广义特征值的广义舒尔 (QZ) 分解

全页折叠

语法

[AA,BB,Q,Z] = qz(A,B)

[AA,BB,Q,Z,V,W] = qz(A,B)

[___] = qz(A,B,mode)

说明

[AA,BB,Q,Z] = qz(A,B) 对方阵 A 和 B 执行 QZ 分解，使得 Q*A*Z = AA 且 Q*B*Z = BB。

如果 A 和 B 是实数，则 AA 和 BB 是上拟三角矩阵。
如果 A 和 B 是复数，则 AA 和 BB 是三角矩阵。
Q 和 Z 是酉矩阵。

示例

[AA,BB,Q,Z,V,W] = qz(A,B) 还返回矩阵 V 和 W，其列分别是 A 和 B 的左右广义特征向量。

示例

如果 mode 是 "real"，则 [___] = qz(A,B,mode) 返回实数分解；如果 mode 是 "complex"，则返回可能的复数分解。可以将此语法与上述语法中的任何输出参量结合使用。

示例

全部折叠

QZ 分解

打开实时脚本

计算两个 3×3 矩阵的 QZ 分解。

A = [1 7 3; 2 9 12; 5 22 7];
B = [3 1 0; 0 3 1; 0 0 3];
[AA,BB,Q,Z] = qz(A,B)

AA = 3×3

   23.5574    1.4134  -14.3485
         0   -0.5776    2.7629
         0         0   -8.6720

BB = 3×3

    3.5845   -0.1090   -0.6024
         0    2.7599    0.8430
         0         0    2.7292

Q = 3×3

    0.2566    0.6353    0.7284
   -0.9477    0.3134    0.0604
   -0.1899   -0.7058    0.6824

Z = 3×3

    0.1502   -0.9664   -0.2088
    0.4689    0.2556   -0.8455
    0.8704    0.0291    0.4915

在计算机精度范围内验证 AA - Q*A*Z、BB - Q*B*Z、Q'*Q - eye(size(Q)) 和 Z'*Z - eye(size(Z)) 的范数是否为 0。

norm(AA - Q*A*Z)

ans = 
6.3184e-15

norm(BB - Q*B*Z)

ans = 
1.7936e-15

norm(Q'*Q - eye(size(Q)))

ans = 
8.8320e-16

norm(Z'*Z - eye(size(Z)))

ans = 
5.1071e-16

广义特征向量

打开实时脚本

计算 QZ 分解，同时返回两个 2×2 矩阵的广义特征向量。

A = [10 -7; -3 2];
B = [7 3; 12 9];
[AA,BB,Q,Z,V,W] = qz(A,B)

AA = 2×2

   11.9600   -4.3532
         0   -0.0836

BB = 2×2

    1.6381   -2.9374
         0   16.4830

Q = 2×2

   -0.9597    0.2811
    0.2811    0.9597

Z = 2×2

   -0.5752    0.8180
    0.8180    0.5752

V = 2×2

   -0.7031    0.6960
    1.0000    1.0000

W = 2×2

   -1.0000    0.2929
    0.4537    1.0000

在计算机精度范围内验证 Q*A*Z - AA 和 Q*B*Z - BB 的元素是否为 0。

Q*A*Z - AA

ans = 2×2
10^-14 ×

         0    0.1776
   -0.1034   -0.1360

Q*B*Z - BB

ans = 2×2
10^-14 ×

   -0.0222         0
    0.0888   -0.3553

使用 eig 函数计算 A 和 B 的广义特征值和左右特征向量。在计算机精度范围内验证 A*V - B*V*D 和 W'*A - D*W'*B 的元素是否为 0。

[V,D,W] = eig(A,B);
A*V - B*V*D

ans = 2×2
10^-14 ×

         0   -0.2297
   -0.7105   -0.0860

W'*A - D*W'*B

ans = 2×2
10^-14 ×

    0.7105   -0.3553
   -0.1235   -0.0625

复数 QZ 分解

打开实时脚本

计算两个 3×3 矩阵的复数 QZ 分解。

A = [1/sqrt(2) 1 0; 0 1 1; 0 1/sqrt(2) 1];
B = [0 1 1; -1/sqrt(2) 0 1; 1 -1/sqrt(2) 0];
[AAc,BBc,Qc,Zc] = qz(A,B)

AAc = 3×3 complex

   0.5011 - 0.8679i   0.0332 - 1.0852i   0.3687 + 0.9278i
   0.0000 + 0.0000i   0.1848 - 0.0000i  -0.6334 - 0.3673i
   0.0000 + 0.0000i   0.0000 + 0.0000i   0.5590 + 0.9682i

BBc = 3×3 complex

   1.0022 + 0.0000i   0.3136 + 0.0711i  -0.0280 + 0.5966i
   0.0000 + 0.0000i   1.3388 + 0.0000i   0.1572 + 0.6846i
   0.0000 + 0.0000i   0.0000 + 0.0000i   1.1180 + 0.0000i

Qc = 3×3 complex

   0.5379 + 0.2210i   0.4604 - 0.3553i   0.3214 - 0.4693i
   0.2172 + 0.3386i   0.4018 - 0.0188i  -0.7698 + 0.2895i
  -0.3719 - 0.6014i   0.7068 - 0.0213i  -0.0000 - 0.0000i

Zc = 3×3 complex

   0.2514 + 0.0413i  -0.7279 - 0.4531i  -0.4470 - 0.0135i
  -0.1000 - 0.6068i   0.3328 - 0.3332i  -0.3326 + 0.5379i
   0.6391 + 0.3853i   0.1423 - 0.1511i   0.2996 + 0.5570i

通过将 mode 指定为 "real，计算 A 和 B 的实数 QZ 分解。A 的广义舒尔形式是拟三角矩阵，表明它具有复数特征值。

[AAr,BBr,Qr,Zr] = qz(A,B,"real")

AAr = 3×3

    0.1464    1.1759    0.3094
         0    1.0360    1.2594
         0   -0.8587    0.3212

BBr = 3×3

    1.0607   -0.5952    0.1441
         0    1.6676         0
         0         0    0.8481

Qr = 3×3

    0.0000   -0.0000   -1.0000
   -0.7882   -0.6154    0.0000
   -0.6154    0.7882   -0.0000

Zr = 3×3

   -0.7071    0.2610   -0.6572
    0.5000   -0.4727   -0.7257
   -0.5000   -0.8417    0.2037

对于三角矩阵 AAc，使用 diag(AA)./diag(BB) 计算特征值。

diag(AAc)./diag(BBc)

ans = 3×1 complex

   0.5000 - 0.8660i
   0.1381 - 0.0000i
   0.5000 + 0.8660i

对于拟三角矩阵 AAr，使用 ordeig 函数计算特征值。

ordeig(AAr,BBr)

ans = 3×1 complex

   0.1381 + 0.0000i
   0.5000 + 0.8660i
   0.5000 - 0.8660i

输入参数

全部折叠

`A`, `B` — 输入矩阵
方阵

输入矩阵，指定为实数方阵或复数方阵。A 和 B 的维度必须相同。

数据类型: single | double
复数支持: 是

`mode` — 分解模式
`"complex"` (默认) | `"real"`

分解模式，指定为下列值之一：

"complex" - qz 返回可能的复数分解，AA 和 BB 是三角矩阵。
"real" - qz 返回实数分解，AA 和 BB 是拟三角矩阵。

输出参量

全部折叠

`AA`, `BB` — `A` 和 `B` 的广义舒尔形式
方阵

A 和 B 的广义舒尔形式，以上三角或拟三角方阵形式返回。

当分解为复数且 AA 为三角矩阵时，则对角线元素 a = diag(AA) 和 b = diag(BB) 是满足 A*V*b = B*V*a 和 b'*W'*A = a'*W'*B 的广义特征值。
当分解为实数且 AA 为拟三角矩阵时，必须进一步约减 2×2 块才能得到全系统的特征值。AA 中的每个 2×2 块对应于 BB 中相同位置的一个 2×2 对角块。

`Q`, `Z` — 酉因子
方阵

酉因子，以满足 Q*A*Z = AA 和 Q*B*Z = BB 的方阵形式返回。

`V` — 右特征向量
方阵

右特征向量，作为方阵返回，其各列为对组 (A,B) 的广义右特征向量。特征向量满足 A*V = B*V*D，其中 D 包含该对组沿其主对角线的广义特征值。使用 eig 函数返回 D，使用 ordeig 函数返回 D 的对角线元素。

不同的计算机和 MATLAB^® 版本可能生成不同的特征向量，它们在数值上依然精确：

对于实数特征向量，特征向量的符号可以更改。
对于复数特征向量，特征向量可以乘以模为 1 的任何复数。
对于多重特征值，其特征向量可以通过线性组合来重新组合。例如，如果 Ax = λx 且 Ay = λy，则 A(x+y) = λ(x+y)，因此 x+y 也是 A 的一个特征向量。

`W` — 左特征向量
方阵

左特征向量，作为方阵返回，其各列为对组 (A,B) 的广义左特征向量。特征向量满足 W'*A = D*W'*B，其中 D 包含该对组沿其主对角线的广义特征值。使用 eig 函数返回 D，使用 ordeig 函数返回 D 的对角线元素。

不同的计算机和 MATLAB 版本可能生成不同的特征向量，它们在数值上依然精确：

对于实数特征向量，特征向量的符号可以更改。
对于复数特征向量，特征向量可以乘以模为 1 的任何复数。
对于多重特征值，其特征向量可以通过线性组合来重新组合。例如，如果 Ax = λx 且 Ay = λy，则 A(x+y) = λ(x+y)，因此 x+y 也是 A 的一个特征向量。

详细信息

全部折叠

拟三角矩阵

上部拟三角矩阵可由实矩阵的舒尔分解或广义舒尔 (QZ) 分解产生。上拟三角矩阵是分块上三角矩阵，沿对角线是由非零值组成的 1×1 和 2×2 分块。

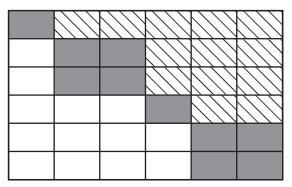
6-by-6 upper quasitriangular matrix with 1-by-1 and 2-by-2 blocks of nonzero values along the diagonal

这些对角块的特征值也是矩阵的特征值。1×1 块对应于实数特征值，2×2 块对应于复共轭特征值对。

酉矩阵

如果可逆复数方阵 U 的共轭转置也是其逆矩阵，即 $U^{*} U = U U^{*} = I$ ，则该矩阵是酉矩阵。

提示

您可以通过 QZ 分解计算求解广义特征值问题 $A x = λ B x$ 的广义特征值。对于三角矩阵 AA，使用 diag(AA)./diag(BB) 计算特征值。对于拟三角矩阵 AA，使用 ordeig(AA,BB) 计算特征值。

扩展功能

全部展开

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

版本历史记录

在 R2006a 之前推出

另请参阅

eig | schur | hess | ordeig

qz

语法

说明

示例

QZ 分解

广义特征向量

复数 QZ 分解

输入参数

A, B — 输入矩阵 方阵

mode — 分解模式 "complex" (默认) | "real"

输出参量

AA, BB — A 和 B 的广义舒尔形式 方阵

Q, Z — 酉因子 方阵

V — 右特征向量 方阵

W — 左特征向量 方阵

详细信息

拟三角矩阵

酉矩阵

提示

扩展功能

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

版本历史记录

另请参阅

`A`, `B` — 输入矩阵
方阵

`mode` — 分解模式
`"complex"` (默认) | `"real"`

`AA`, `BB` — `A` 和 `B` 的广义舒尔形式
方阵

`Q`, `Z` — 酉因子
方阵

`V` — 右特征向量
方阵

`W` — 左特征向量
方阵

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。