std
标准差
语法
说明
S = std(A)A 沿大小不等于 1 的第一个数组维度的元素的标准差。默认情况下,标准差按 N-1 实现归一化,其中 N 是观测值数量。
如果
A是观测值的向量,则S是标量。如果
A是一个列为随机变量且行为观测值的矩阵,则S是一个包含与每列对应的标准差的行向量。如果
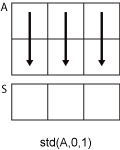
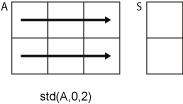
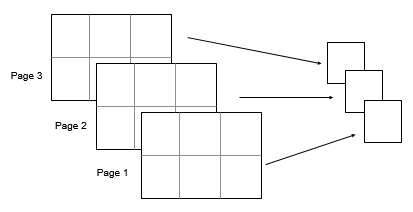
A是多维数组,则std(A)沿大小不等于 1 的第一个数组维度计算,并将这些元素视为向量。此维度中S的大小变为1,而所有其他维度的大小仍与在A中相同。如果
A是标量,则S为0。如果
A是一个0×0的空数组,则S为NaN。如果
A是表或时间表,则std(A)返回单行表,其中包含每个变量的标准差。 (自 R2023a 起)
S = std(___,missingflag)A 中的缺失值。例如,std(A,"omitmissing") 在计算标准差时会忽略所有缺失值。默认情况下,std 包括缺失值。