使用 `pagefun` 提高 GPU 上小矩阵问题的性能

此示例说明如何使用 pagefun 来提高对多维数组中排列的多个矩阵施加独立运算的性能。

多维数组是二维矩阵的扩展，使用额外的下标进行索引。例如，三维数组使用三个下标。前两个维度表示矩阵，第三个维度表示元素页面（有时称为切片）。有关详细信息，请参阅多维数组。

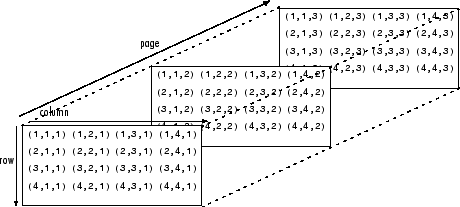
虽然 GPU 可以有效地将小型独立操作应用于大型矩阵，但当这些操作以串行方式应用时（例如，当在 for 循环中应用这些操作时），性能并不理想。为了避免串行处理，arrayfun函数在 GPU 上并行对数组的每个元素应用标量运算。类似地，pagefun 函数将一个函数应用于多维 GPU 数组的每个页面。

pagefun 函数支持应用大多数元素函数和许多支持 GPU 数组输入的矩阵运算。MATLAB® 还提供了许多专用的页面函数，包括 pagemtimes、pagemldivide、pagemrdivide、pagetranspose、pagectranspose、pageinv、pagenorm 和 pagesvd。根据任务的不同，这些函数可能会简化您的代码或提供比使用 pagefun 更好的性能。

在这个示例中，计算机人正在导航一个已知地图，该地图包含大量计算机人可以使用其传感器识别的特征。计算机人通过测量这些特征的相对位置和方向并将它们与地图位置进行比较来确定地图上的定位。假设计算机人没有完全迷失，它可以利用两者之间的任何差异来纠正其位置，例如通过使用卡尔曼滤波器。这个示例展示了一种计算相对于计算机人的特征位置的有效方法。

设置地图

定义包含许多特征的房间的维度。

roomDimensions = [50 50 5];

本示例末尾提供了支持函数 randomTransforms，并用随机值初始化 N 变换，提供一个结构体作为输出。它使用 3×1 向量 T 和 3×3 旋转矩阵 R 来表示位置和方向。N 平移被打包成一个 3×N 矩阵，而旋转被打包成一个 3×3×N 数组。

使用 randomTransforms 函数设置 1000 特征的地图以及计算机人的起始位置。

numFeatures = 1000;
Map = randomTransforms(numFeatures,roomDimensions);
Robot = randomTransforms(1,roomDimensions);

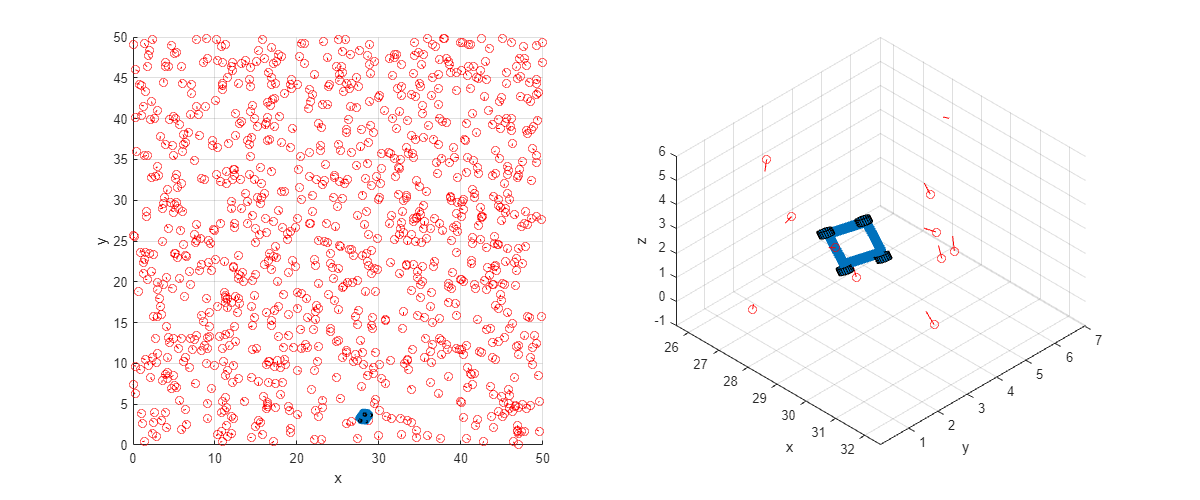
plotRobot 函数作为本示例的支持文件提供，绘制了房间的俯视图以及计算机人和附近特征的近距离视图。计算机人用一个带轮子的蓝色盒子表示，特征用红色圆圈表示，伴随的线条表示它们的方向。要使用此函数，请将示例作为 livescript 打开。

调用 plotRobot 函数。

plotRobot(Robot,Map)

定义方程

为了正确识别地图中的特征，计算机人需要转换地图以将其传感器置于原点。然后，它可以通过比较所看到的内容与期望看到的内容来找到地图特征。

对于地图特征 $i$ ，我们可以通过转换其全局地图位置来找到它相对于计算机人 $T_{r e l} (i)$ 的位置和方向 $R_{r e l} (i)$ ：

$\begin{array}{l} R_{r e l} (i) = R_{b o t}^{⊤} R_{m a p} (i) \\ T_{r e l} (i) = R_{b o t}^{⊤} (T_{m a p} (i) - T_{b o t}) \end{array}$

其中 $T_{b o t}$ 和 $R_{b o t}$ 是计算机人的位置和方向， $T_{m a p} (i)$ 和 $R_{m a p} (i)$ 表示地图数据。等效的 MATLAB 代码如下所示：

Rrel(:,:,i) = Rbot' * Rmap(:,:,i)
Trel(:,i) = Rbot' * (Tmap(:,i) - Tbot)

在 CPU 上使用 `for` 循环执行矩阵变换

本示例末尾提供了支持函数 loopingTransform，依次循环遍历所有变换，将每个特征变换到其相对于计算机人的位置。注意 like 函数的 zeros 名称-值参量，它使函数返回与原型数组相同数据类型的零数组。例如，如果原型数组是 gpuArray，那么 zeros 将返回 gpuArray。这使得您可以在下一节中在 GPU 上使用相同的代码。

使用timeit函数对计算进行计时。timeit 函数对 loopingTransform 的执行进行多次计时，并返回测量值的中值。由于 timeit 需要一个没有参量的函数，因此使用 @() 语法来创建正确形式的匿名函数。

cpuTime = timeit(@()loopingTransform(Robot,Map,numFeatures))

cpuTime = 0.0042

使用 `for` 循环在 GPU 上执行矩阵变换

要在 GPU 上运行相同的代码，只需将输入数据作为 gpuArray 传递给函数。gpuArray 代表存储在 GPU 内存中的数组。MATLAB 和其他工具箱中的许多函数都支持 gpuArray 对象，允许您以最少的代码更改在 GPU 上运行代码。有关详细信息，请参阅在 GPU 上运行 MATLAB 函数。

确保您想要的 GPU 可用且已被选择。

gpu = gpuDevice;
disp(gpu.Name + " GPU selected.")

NVIDIA RTX A5000 GPU selected.

创建包含计算机人的位置和方向以及地图中的特征的 GPU 数组。

gMap.R = gpuArray(Map.R);
gMap.T = gpuArray(Map.T);
gRobot.R = gpuArray(Robot.R);
gRobot.T = gpuArray(Robot.T);

使用gputimeit函数对计算进行计时。对于包含 GPU 计算的代码，gputimeit 函数相当于 timeit。它确保在记录时间之前所有 GPU 操作都已完成。

gpuTime = gputimeit(@()loopingTransform(gRobot,gMap,numFeatures))

gpuTime = 0.1905

使用 `pagefun` 在 GPU 上执行矩阵变换

GPU 版本非常慢，因为尽管所有计算都是独立的，但它们都是串行运行的。使用 pagefun 我们可以并行运行所有计算。

本示例末尾提供了支持函数 pagefunTransform，它应用与 loopingTransform 函数相同的变换，但使用 pagefun 而不是 for 循环。第一个计算是旋转的计算。这涉及矩阵乘法，转换为函数 mtimes (*)。将其与要相乘的两组旋转一起传递给 pagefun：

Rel.R = pagefun(@mtimes,Robot.R',Map.R);

Robot.R' 是一个 3×3 矩阵，而 Map.R 是一个 3×3×N 数组。pagefun 函数将地图中的每个独立矩阵与相同的计算机人旋转进行匹配，并为我们提供所需的 3×3×N 输出。

平移计算也涉及矩阵乘法，但矩阵乘法的正常规则允许它在循环之外进行而不进行任何更改：

Rel.T = Robot.R' * (Map.T - Robot.T);

使用gputimeit函数对计算进行计时。

gpuPagefunTime = gputimeit(@()pagefunTransform(gRobot,gMap))

gpuPagefunTime = 3.3066e-04

比较结果

绘制时序结果。

figure
labels = categorical(["CPU Execution","GPU Execution","GPU Execution with \fontname{consolas}pagefun"]);
bar(labels,[cpuTime,gpuTime,gpuPagefunTime])
ylabel("Execution Time (s)")
set(gca,YScale="log")

计算使用 pagefun 的执行比 CPU 和简单的 GPU 执行快多少。

fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than on the CPU.\n", ...
    cpuTime/gpuPagefunTime);

Executing the transforms on the GPU using pagefun is 12.65 times faster than on the CPU.

fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than using for-loops on the GPU.\n", ...
    gpuTime/gpuPagefunTime);

Executing the transforms on the GPU using pagefun is 576.17 times faster than using for-loops on the GPU.

使用多个可能的计算机人位置来定位丢失的计算机人

如果计算机人位于地图的未知部分，它可以使用全局搜索算法来定位自己。该算法通过执行上述计算并寻找计算机人传感器看到的特征与计算机人期望在该位置看到的特征之间的良好对应关系来测试许多可能的位置。

现在计算机人有多个可能的位置以及多个特征。N 个特征和 M 个计算机人需要 N*M 转换。为了区分“计算机人空间”和“特征空间”，使用第 4 维进行旋转，使用第 3 个维度进行平移。这意味着计算机人的旋转将是 3×3×1×M，平移将是 3×1×M。

使用十个随机计算机人位置初始化搜索。好的搜索算法会使用拓扑或其他线索来更智能地进行搜索。

numRobots = 10;
Robot = randomTransforms(numRobots,roomDimensions);
Robot.R = reshape(Robot.R,3,3,1,[]); % Spread along the 4th dimension
Robot.T = reshape(Robot.T,3,1,[]); % Spread along the 3rd dimension

本示例末尾定义了一个支持函数 loopingTransform2，它使用两个嵌套循环执行循环转换，以循环遍历计算机人和特征。

使用 timeit 来计算时间。

cpuTime = timeit(@()loopingTransform2(Robot,Map,numFeatures,numRobots))

cpuTime = 0.0759

创建包含计算机人旋转和平移的 GPU 数组。

gRobot.R = gpuArray(Robot.R);
gRobot.T = gpuArray(Robot.T);

使用 gputimeit 对 GPU 上的计算进行计时。

gpuTime = gputimeit(@() loopingTransform2(gRobot,gMap,numFeatures,numRobots))

gpuTime = 2.1059

与以前一样，循环版本在 GPU 上的运行速度要慢得多，因为它不并行进行计算。

本示例末尾提供了一个支持函数 pagefunTransform2，它使用两个 loopingTransform2 调用而不是嵌套的 pagefun 循环应用与 for 函数相同的转换。此函数需要将 transpose 运算符以及 mtimes 合并到对 pagefun 的调用中。该函数还将 squeeze 函数应用于转置的计算机人方向，以将计算机人的分布放入第 3 个维度，从而匹配平移。尽管如此，最终的代码还是更加紧凑。

pagefun 函数会适当扩展维度，因此当我们将 3×3×1×M 矩阵 Rt 与 3×3×N×1 矩阵 Map.R 相乘时，我们得到一个 3×3×N×M 矩阵。

使用 gputimeit 对 GPU 上的计算进行计时。

gpuPagefunTime = gputimeit(@()pagefunTransform2(gRobot,gMap))

gpuPagefunTime = 0.0014

比较结果

绘制时序结果。

labels = categorical(["CPU Execution","GPU Execution","GPU Execution with \fontname{consolas}pagefun"]);
bar(labels,[cpuTime,gpuTime,gpuPagefunTime])
ylabel("Execution Time (s)")
set(gca,YScale="log")

fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than on the CPU.\n", ...
    cpuTime/gpuPagefunTime);

Executing the transforms on the GPU using pagefun is 55.85 times faster than on the CPU.

fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than using nested for-loops on the GPU.\n", ...
    gpuTime/gpuPagefunTime);

Executing the transforms on the GPU using pagefun is 1549.19 times faster than using nested for-loops on the GPU.

结论

pagefun 函数支持许多二维运算，以及 arrayfun 支持的大多数标量运算。通过这些函数，您可以对涉及矩阵代数和数组操作的一系列计算进行向量化，从而无需循环并可获得巨大的性能提升。

无论您在循环中对 GPU 数据进行小规模计算，都应该考虑以这种方式转换为向量化实现。这也是一个利用 GPU 来提高性能的机会，而之前 GPU 并没有带来任何性能提升。

支持函数

随机变换函数

randomTransforms 函数在指定维度的房间中创建定义 N 随机变换的矩阵。每个变换包括一个随机平移 T 和一个随机旋转 R。该函数可用于设置房间特征地图以及计算机人的起始位置和方向。

function Tform = randomTransforms(N,roomDimensions)
% Preallocate matrices.
Tform.T = zeros(3,N);
Tform.R = zeros(3,3,N);

for i = 1:N
    % Create random translation.
    Tform.T(:,i) = rand(3,1) .* roomDimensions';

    % Create random rotation by extracting an orthonormal
    % basis from a random 3-by-3 matrix.
    Tform.R(:,:,i) = orth(rand(3,3));
end

end

循环变换函数

loopingTransform 函数通过依次循环变换将每个特征转换为其相对于计算机人的位置。

function Rel = loopingTransform(Robot,Map,numFeatures)
% Preallocate matrices.
Rel.R = zeros(size(Map.R),like=Map.R);
Rel.T = zeros(size(Map.T),like=Map.T);

for i = 1:numFeatures
    % Find orientation of map feature relative to the robot.
    Rel.R(:,:,i) = Robot.R' * Map.R(:,:,i);
    % Find position of map feature relative to the robot.
    Rel.T(:,i) = Robot.R' * (Map.T(:,i) - Robot.T);
end

end

`pagefun` 变换函数

pagefunTransform 函数通过使用 pagefun 函数应用变换将每个特征变换到其相对于计算机人的位置。

function Rel = pagefunTransform(Robot,Map)
% Find orientation of map feature relative to the robot.
Rel.R = pagefun(@mtimes,Robot.R', Map.R);
% Apply translation.
Rel.T = Robot.R' * (Map.T - Robot.T);
end

嵌套循环转换函数

loopingTransform2 函数使用两个嵌套循环执行循环转换，循环遍历计算机人以及特征。变换将每个特征映射到相对于每个计算机人的位置。

function Rel = loopingTransform2(Robot,Map,numFeatures,numRobots)
% Preallocate matrices.
Rel.R = zeros(3,3,numFeatures,numRobots,like=Map.R);
Rel.T = zeros(3,numFeatures,numRobots,like=Map.T);

for i = 1:numFeatures
    for j = 1:numRobots
        % Find orientation of map feature relative to the robot.
        Rel.R(:,:,i,j) = Robot.R(:,:,1,j)' * Map.R(:,:,i);
        % Find position of map feature relative to the robot.
        Rel.T(:,i,j) = ...
            Robot.R(:,:,1,j)' * (Map.T(:,i) - Robot.T(:,1,j));
    end
end

end

两次调用 `pagefun` 转换函数

pagefunTransform2 函数通过两次调用 pagefun 函数执行转换，将每个特征映射到相对于每个计算机人的位置。

function Rel = pagefunTransform2(Robot,Map)
% Find orientation of map feature relative to the robot.
Rt = pagefun(@transpose,Robot.R);
Rel.R = pagefun(@mtimes,Rt,Map.R);
% Find position of map feature relative to the robot.
Rel.T = pagefun(@mtimes,squeeze(Rt), ...
    (Map.T - Robot.T));
end

另请参阅

pagefun | gpuArray | arrayfun | gputimeit

使用 pagefun 提高 GPU 上小矩阵问题的性能

设置地图

定义方程

在 CPU 上使用 for 循环执行矩阵变换

使用 for 循环在 GPU 上执行矩阵变换

使用 pagefun 在 GPU 上执行矩阵变换

比较结果

使用多个可能的计算机人位置来定位丢失的计算机人

比较结果

结论

支持函数

随机变换函数

循环变换函数

pagefun 变换函数

嵌套循环转换函数

两次调用 pagefun 转换函数

另请参阅

主题

使用 `pagefun` 提高 GPU 上小矩阵问题的性能

在 CPU 上使用 `for` 循环执行矩阵变换

使用 `for` 循环在 GPU 上执行矩阵变换

使用 `pagefun` 在 GPU 上执行矩阵变换

`pagefun` 变换函数

两次调用 `pagefun` 转换函数