pagemtimes

按页矩阵乘法

自 R2020b 起

全页折叠

语法

Z = pagemtimes(X,Y)

Z = pagemtimes(X,transpX,Y,transpY)

说明

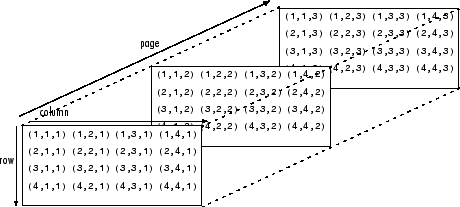
Z = pagemtimes(X,Y) 计算 N 维数组 X 和 Y 的对应页的矩阵乘积。输出数组 Z 的每页都由乘积给出：Z(:,:,i) = X(:,:,i)*Y(:,:,i)。

如果 X 或 Y 之一是矩阵，则 pagemtimes 将其与另一输入的每页相乘。例如，如果 X 是矩阵，则 Z(:,:,i) = X*Y(:,:,i)。
如果 X 和 Y 有三个以上的维度，则前两个维度以外的所有维度都必须具有兼容大小。pagemtimes 隐式扩展额外的维度，以乘以分页矩阵的所有组合：Z(:,:,i,j,k) = Xx(:,:,i,j,k)*Yy(:,:,i,j,k)。（额外维度已在 Xx 和 Yy 中扩展。）

示例

Z = pagemtimes(X,transpX,Y,transpY) 可以选择使用 X 和 Y 的指定转置来计算矩阵乘积。对于此语法，您必须指定两个转置选项。transpX 和 transpY 必须分别为：'transpose'、'ctranspose' 或 'none'。

示例

全部折叠

乘以三维数组

打开实时脚本

创建两个三维数组，并乘以对应的页。

rng default
X = randi([1 6],2,2,3)

X = 
X(:,:,1) =

     5     1
     6     6


X(:,:,2) =

     4     2
     1     4


X(:,:,3) =

     6     1
     6     6

Y = randi([1 6],2,2,3)

Y = 
Y(:,:,1) =

     6     5
     3     1


Y(:,:,2) =

     3     5
     6     6


Y(:,:,3) =

     4     6
     1     6

Z = pagemtimes(X,Y)

Z = 
Z(:,:,1) =

    33    26
    54    36


Z(:,:,2) =

    24    32
    27    29


Z(:,:,3) =

    25    42
    30    72

输出 Z(:,:,i) 的第 i 页通过乘以 X(:,:,i)*Y(:,:,i) 而形成。

乘以矩阵和三维数组

打开实时脚本

创建一个矩阵 A 和一个三维数组 Y，然后将该三维数组的每页与该矩阵相乘。

A = magic(3)

A = 3×3

     8     1     6
     3     5     7
     4     9     2

rng default
Y = randi([1 10],3,3,3)

Y = 
Y(:,:,1) =

     9    10     3
    10     7     6
     2     1    10


Y(:,:,2) =

    10    10     2
     2     5     5
    10     9    10


Y(:,:,3) =

     8     1     7
    10     9     8
     7    10     8

Z = pagemtimes(A,Y)

Z = 
Z(:,:,1) =

    94    93    90
    91    72   109
   130   105    86


Z(:,:,2) =

   142   139    81
   110   118   101
    78   103    73


Z(:,:,3) =

   116    77   112
   123   118   117
   136   105   116

输出 Z(:,:,i) 的第 i 页通过乘以 A*Y(:,:,i) 而形成。

乘以转置后的数组页

打开实时脚本

创建两个三维数组 X 和 Y。使用 pagemtimes 对 X 和 Y 的每页执行运算 X(:,:,i)'*Y(:,:,i)。

rng default
X = rand(3,3,3) + 1i;
Y = rand(3,3,3);
A = pagemtimes(X,'ctranspose',Y,'none')

A = 
A(:,:,1) =

   0.9350 - 1.2189i   0.6392 - 1.0148i   0.2302 - 0.9668i
   0.7894 - 1.2189i   0.6920 - 1.0148i   0.1839 - 0.9668i
   0.6316 - 1.2189i   0.4792 - 1.0148i   0.8544 - 0.9668i


A(:,:,2) =

   1.6427 - 1.9622i   0.4727 - 0.8547i   1.0453 - 1.7476i
   1.5794 - 1.9622i   0.5513 - 0.8547i   1.2682 - 1.7476i
   1.1025 - 1.9622i   0.5393 - 0.8547i   0.6151 - 1.7476i


A(:,:,3) =

   1.2393 - 1.5817i   1.4671 - 1.7401i   1.2737 - 1.4974i
   0.9995 - 1.5817i   0.9240 - 1.7401i   0.7324 - 1.4974i
   1.1504 - 1.5817i   1.2585 - 1.7401i   1.0786 - 1.4974i

现在，对 X 和 Y 的每页执行运算 X(:,:,i)*Y(:,:,i).'。

B = pagemtimes(X,'none',Y,'transpose')

B = 
B(:,:,1) =

   0.9773 + 1.1444i   0.5902 + 0.7844i   0.6217 + 1.2716i
   0.8270 + 1.1444i   0.6670 + 0.7844i   0.7805 + 1.2716i
   0.1629 + 1.1444i   0.1793 + 0.7844i   0.8372 + 1.2716i


B(:,:,2) =

   0.8120 + 1.4948i   0.8387 + 1.5510i   1.3086 + 1.5187i
   0.4491 + 1.4948i   0.5983 + 1.5510i   0.4138 + 1.5187i
   1.4030 + 1.4948i   1.3871 + 1.5510i   1.3988 + 1.5187i


B(:,:,3) =

   0.8747 + 1.8788i   0.8246 + 1.8554i   0.6322 + 1.0849i
   1.5873 + 1.8788i   1.5648 + 1.8554i   0.9777 + 1.0849i
   1.4888 + 1.8788i   1.4839 + 1.8554i   0.8025 + 1.0849i

将 N 维数组相乘

打开实时脚本

创建一个 3×3×2 数组 X，并将其与 3×3×1×4 数组 Y 相乘。结果大小为 3×3×2×4。

X = ones(3,3,2);
A = eye(3);
Y = cat(4,A,2*A,3*A,4*A);
Z = pagemtimes(X,Y)

Z = 
Z(:,:,1,1) =

     1     1     1
     1     1     1
     1     1     1


Z(:,:,2,1) =

     1     1     1
     1     1     1
     1     1     1


Z(:,:,1,2) =

     2     2     2
     2     2     2
     2     2     2


Z(:,:,2,2) =

     2     2     2
     2     2     2
     2     2     2


Z(:,:,1,3) =

     3     3     3
     3     3     3
     3     3     3


Z(:,:,2,3) =

     3     3     3
     3     3     3
     3     3     3


Z(:,:,1,4) =

     4     4     4
     4     4     4
     4     4     4


Z(:,:,2,4) =

     4     4     4
     4     4     4
     4     4     4

大小为 1 的每个维度（在前两个维度后）会隐式扩展以匹配另一个输入的维度大小，然后通过乘以 X(:,:,i,j)*Y(:,:,i,j) 而形成输出 Z(:,:,i,j) 的每页。此运算的一种直观考虑方式是，X 在三维数组中包含两个矩阵作为页，Y 包含四个沿第四个维度排列的矩阵；因此，将这些矩阵的所有组合相乘得到八个 3×3 矩阵。

输入参数

全部折叠

`X`, `Y` — 输入数组
矩阵 | 多维数组

输入数组，指定为稠密矩阵或多维数组。X 和 Y 的页必须为矩阵乘积 (mtimes, *) 的有效输入。

如果 X 或 Y 之一是矩阵，则 pagemtimes 将其与另一输入的每页相乘。例如，如果 X 是矩阵，则 Z(:,:,i) = X*Y(:,:,i)。
如果 X 和 Y 有三个以上的维度，则前两个维度以外的所有维度都必须具有兼容大小。pagemtimes 隐式扩展额外的维度，以乘以分页矩阵的所有组合：Z(:,:,i,j,k) = Xx(:,:,i,j,k)*Yy(:,:,i,j,k)。（额外维度已在 Xx 和 Yy 中扩展。）

数据类型: single | double
复数支持: 是

`transpX`, `transpY` — 转置选项
`'none'` (默认) | `'transpose'` | `'ctranspose'`

转置选项，每个选项都指定为下表中的值之一。

值	描述
`'none'`	不要应用转置。
`'transpose'`	将转置应用于对应输入的每页（`transpose` 应用于每页）。
`'ctranspose'`	将复共轭转置应用于对应输入的每页（`ctranspose` 应用于每页）。

使用转置选项以按页方式计算运算，如 X'*Y。即使只对一个输入进行转置，您也必须指定两个转置选项。

示例: pagemtimes(X,'ctranspose',Y,'none') 计算 X'*Y 的按页版本。

数据类型: char | string

输出参量

全部折叠

`Z` — 输出数组
多维数组

输出数组，以多维数组形式返回。pagemtimes 执行的运算取决于输入 X 和 Y 的大小：

`X` 的大小	`Y` 的大小	运算
三维	三维	`Z(:,:,i) = X(:,:,i)*Y(:,:,i)`
二维	三维	`Z(:,:,i) = X*Y(:,:,i)`
三维	二维	`Z(:,:,i) = X(:,:,i)*Y`
N 维	N 维	`Z(:,:,i,j,k) = X(:,:,i,j,k)*Y(:,:,i,j,k)`

Z 的大小遵循以下规则：

在前两个维度中，适用矩阵乘法规则。如果任一操作数是标量，则结果具有非标量操作数的大小。当两个操作数均为矩阵时，将 m×n 矩阵乘以 n×q 矩阵会得到 m×q 矩阵。
X 和 Y 中前两个维度之外的兼容维度会扩展以匹配非单一维度。因此，如果 X 为 10×8×1×3，Y 为 8×10×4×1，则 Z 为 10×10×4×3。

详细信息

全部折叠

数组页

像 pagemtimes 这样的分页运算函数对排列成一个多维数组的二维矩阵进行运算。例如，三维数组的第三个维度中的元素通常称为页面，因为它们像书籍中的页一样堆叠在一起。每个页面都是函数对其进行运算的一个矩阵。

您也可以将二维矩阵的集合组合成一个更高维度的数组，如四维或五维数组，在这种情况下，pagemtimes 仍将数组的基本单位视为可对其进行函数运算的一个二维矩阵，如 X(:,:,i,j,k,l)。

cat 函数可用于将矩阵集合组合成一个多维数组，而 zeros 函数可用于预分配一个多维数组。

提示

对于实数和复数 N 维数组，pagemtimes(X,'transpose',X,'none') 和 pagemtimes(X,'none',X,'transpose') 返回具有对称矩阵页的数组。对于复数 N 维数组，pagemtimes(X,'ctranspose',X,'none') 和 pagemtimes(X,'none',X,'ctranspose') 返回具有埃尔米特矩阵页的数组。
使用 pagemtimes 获得的结果在数值上等效于在 for 循环中乘以每个相同的矩阵。但是，由于存在浮点舍入误差，这两个结果可能略有不同。

扩展功能

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

转置选项 transpX 和 transpY 必须为常量。
代码生成不支持对此函数使用整数和半精度数据类型。
传递给 pagemtimes 的输入数组必须为非稀疏数组。
代码生成支持数组输入沿 pagemtimes 函数的非页维度的隐式扩展。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

用法说明和限制：

转置选项 transpX 和 transpY 必须为常量。
代码生成不支持对此函数使用整数和半精度数据类型。
传递给 pagemtimes 的输入数组必须为非稀疏数组。
代码生成支持数组输入沿 pagemtimes 函数的非页维度的隐式扩展。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

此函数完全支持 GPU 数组。有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

此函数完全支持分布式数组。有关详细信息，请参阅使用分布式数组运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2020b 中推出

另请参阅

mtimes | tensorprod | pagectranspose | pagetranspose

主题

多维数组

pagemtimes

语法

说明

示例

乘以三维数组

乘以矩阵和三维数组

乘以转置后的数组页

将 N 维数组相乘

输入参数

X, Y — 输入数组 矩阵 | 多维数组

transpX, transpY — 转置选项 'none' (默认) | 'transpose' | 'ctranspose'

输出参量

Z — 输出数组 多维数组

详细信息

数组页

提示

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成 使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

另请参阅

主题

WeChat

`X`, `Y` — 输入数组
矩阵 | 多维数组

`transpX`, `transpY` — 转置选项
`'none'` (默认) | `'transpose'` | `'ctranspose'`

`Z` — 输出数组
多维数组

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。