SimBiology.Scenarios

Simulation scenarios

Description

SimBiology.Scenarios is an object that lets you generate different simulation scenarios based on different sample values of model quantities. You can combine these quantities with different doses or variants and simulate various scenarios to explore model behaviors under different experimental conditions and dosing regimens.

Creation

Syntax

sObj = SimBiology.Scenarios

sObj = SimBiology.Scenarios(name,content)

sObj = SimBiology.Scenarios(quantityNames,probDist,Name,Value)

Description

sObj = SimBiology.Scenarios returns a Scenarios object sObj that contains no entries.

example

sObj = SimBiology.Scenarios(name,content) returns a Scenarios object sObj with one entry. name is the name of a model quantity or the name of a group of variants or doses for scenario generation. content contains the corresponding numeric values for the model quantity or a vector of variant objects or vector of dose objects.

example

sObj = SimBiology.Scenarios(quantityNames,probDist,Name,Value) specifies to generate the sample values for one or more model quantities quantityNames from the joint probability distribution probDist. Specify additional options for the probability distributions and sampling method using one or more name-value pair arguments. To specify the probability distributions, you must have Statistics and Machine Learning Toolbox™.

example

Input Arguments

expand all

`name` — Entry name
character vector | string

Entry name, specified as a character vector or string.

You can set the entry name to the name of a model quantity (species, parameter, or compartment). Alternatively, you can define a name for a group of doses or variants to be included in the sample (scenarios) generation.

Example: "k1"

Data Types: char | string

`content` — Model quantity values or vector of doses or variants
numeric vector | vector of `RepeatDose` or `ScheduleDose` objects | vector of variant objects

Model quantity values, or a vector of doses or variants, specified as a numeric vector, vector of RepeatDose or ScheduleDose objects, or vector of variant objects.

If you specify a quantity name for the name input argument, set content to a numeric vector.

If you specify a name for a group of doses or variants, set content to a vector of dose objects or vector of variant objects.

Example: [0.5,1,1.5]

`quantityNames` — Names of model quantities
character vector | string | string vector | cell array of character vectors

Names of model quantities for the sample (scenario) generation, specified as a character vector, string, string vector, or cell array of character vectors.

Example: ["k12","k21"]

Data Types: char | string | cell

`probDist` — Probability distributions
vector of probability distribution objects | character vector | string | string vector | cell array of character vectors

Probability distributions to generate sample values for model quantities, specified as a vector of probability distribution objects, character vector, string, string vector, or cell array of character vectors containing the names of supported probability distributions. To specify the probability distributions, you must have Statistics and Machine Learning Toolbox.

Use the makedist (Statistics and Machine Learning Toolbox) function to create distribution objects. For a list of supported distributions, see distname (Statistics and Machine Learning Toolbox).

Example: [pd1,pd2]

Name-Value Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside quotes. You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

Example: 'Number',10 specifies to generate 10 samples.

`Number` — Number of samples
`[]` (default) | positive scalar

Number of samples to draw from probability distributions, specified as the comma-separated pair consisting of 'Number' and a positive scalar. The default value [] means that the function infers the number of samples from other entries. If the number cannot be inferred, the number is set to 2.

Example: 'Number',5

`RankCorrelation` — Rank correlation matrix
`[]` (default) | numeric matrix

Rank correlation matrix for the joint probability distribution, specified as the comma-separated pair consisting of 'RankCorrelation' and a numeric matrix. The default behavior is that when both 'RankCorrelation' and 'Covariance' are set to [], SimBiology.Scenarios draws uncorrelated samples from the joint probability distribution.

You cannot specify 'RankCorrelation' if 'Covariance' is set. The number of columns in the matrix must match the number of specified distributions. The matrix must be symmetric with diagonal values of 1. All of its eigenvalues must also be positive.

Example: 'RankCorrelation',[1 0.3;0.3 1]

`Mean` — Mean values
numeric vector

Mean values of quantities, specified as the comma-separated pair consisting of 'Mean' and a numeric vector.

You can specify mean values for normal distributions only. The number of mean values must equal the number of specified probability distributions.

Example: 'Mean',[0.5,1.5]

`Covariance` — Covariance matrix
`[]` (default) | numeric matrix

Covariance matrix for the joint probability distribution, specified as the comma-separated pair consisting of 'Covariance' and a numeric matrix. The default behavior is that if both 'RankCorrelation' and 'Covariance' are set to [], SimBiology.Scenarios draws uncorrelated samples from the joint probability distribution. You cannot specify 'Covariance' if you specify 'RankCorrelation'.

You can specify the covariance matrix for normal distributions only. The number of columns in the matrix must match the number of specified distributions. All of its eigenvalues must also be nonnegative.

Example: 'Covariance',[0.25 0.15;0.15 0.25]

`SamplingMethod` — Sampling method
`'random'` (default) | `'lhs'` | `'copula'` | `'sobol'` | `'halton'`

Sampling method, specified as the comma-separated pair consisting of 'SamplingMethod' and a character vector or string. Depending on whether probability distributions with 'RankCorrelation' or normal distributions with 'Covariance' are specified, the sampling techniques differ.

If an entry contains a (joint) normal distribution with Covariance specified, the sampling methods are:

'random' – Draw random samples from the specified normal distribution using mvnrnd (Statistics and Machine Learning Toolbox).
'lhs' – Draw Latin hypercube samples from the specified normal distributions using lhsnorm (Statistics and Machine Learning Toolbox). For details, see Generating Quasi-Random Numbers (Statistics and Machine Learning Toolbox).

If an entry contains a (joint) distribution with no Covariance specified, the sampling methods are:

'random' – Draw random samples from the specified probability distributions using random (Statistics and Machine Learning Toolbox).
'lhs' – Draw Latin hypercube samples from the specified probability distributions using an algorithm similar to lhsdesign (Statistics and Machine Learning Toolbox). This approach is a more systematic space-filling approach than random sampling. For details, see Generating Quasi-Random Numbers (Statistics and Machine Learning Toolbox).
'copula' – Draw random samples using a copula (Statistics and Machine Learning Toolbox). Use this option to impose correlations between samples using copulas.
'sobol' – Use the sobol sequence (sobolset (Statistics and Machine Learning Toolbox)) which is transformed using the inverse cumulative distribution function (icdf (Statistics and Machine Learning Toolbox)) of the specified probability distributions. Use this method for highly systematic space-filling. For details, see Generating Quasi-Random Numbers (Statistics and Machine Learning Toolbox).
'halton' – Use the halton sequence (haltonset (Statistics and Machine Learning Toolbox)) which is transformed using the inverse cumulative distribution function (icdf (Statistics and Machine Learning Toolbox)) of the specified probability distributions. For details, see Generating Quasi-Random Numbers (Statistics and Machine Learning Toolbox).

If no Covariance is specified, SimBiology.Scenarios essentially performs two steps. The first step is to generate samples using one of the above sampling methods. For lhs, sobol, and halton methods, the generated uniform samples are transformed to samples from the specified distribution using the inverse cumulative distribution function icdf (Statistics and Machine Learning Toolbox). Then, as the second step, the samples are correlated using the Iman-Conover algorithm if RankCorrelation is specified. For random, the samples are drawn directly from the specified distributions and the samples are then correlated using the Iman-Conover algorithm.

Example: 'SamplingMethod','lhs'

`SamplingOptions` — Options for sampling method
struct

Options for the sampling method, specified as a scalar struct. The options differ depending on the sampling method: sobol, halton, or lhs.

For sobol and halton, specify each field name and value of the structure according to each name-value argument of the sobolset (Statistics and Machine Learning Toolbox) or haltonset (Statistics and Machine Learning Toolbox) function. SimBiology uses the default value of 1 for the Skip argument for both methods. For all other name-value arguments, the software uses the same default values of sobolset or haltonset. For instance, set up a structure for the Leap and Skip options with nondefault values as follows.

s1.Leap = 50;
s1.Skip = 0;

For lhs, there are three samplers that support different sampling options.

If you specify a covariance matrix, SimBiology uses lhsnorm (Statistics and Machine Learning Toolbox) for sampling. SamplingOptions argument is not allowed.
Otherwise, use the field name UseLhsdesign to select a sampler.
- If the value is true, SimBiology uses lhsdesign (Statistics and Machine Learning Toolbox). You can use the name-value arguments of lhsdesign to specify the field names and values.
- If the value is false (default), SimBiology uses a nonconfigurable Latin hypercube sampler that is different from lhsdesign. This sampler does not require Statistics and Machine Learning Toolbox. SamplingOptions cannot contain any other options, except UseLhsdesign.

For instance, set up a structure to use lhsdesign with the Criterion and Iterations options.

s2.UseLhsdesign  = true;
s2.Criterion     = "correlation";
s2.Iterations    = 10;

You cannot specify sampling options for the random and copula methods.

Data Types: struct

Properties

expand all

`Expression` — Combination expression
character vector

This property is read-only.

Combination expression summarizing the combination of entries in the object, specified as a character vector. The plus + sign indicates the elementwise combination, and the cross x sign indicates the cartesian combination. For details, see Combine Simulation Scenarios in SimBiology.

Example: '(k1 + k2 + k3) x doses'

Data Types: char

`NumberOfEntries` — Number of entries
positive integer

Number of entries in the scenarios object, specified as a positive integer.

Example: 4

Data Types: double

`RandomSeed` — Seed or state for random number generation
`[]` (default) | nonnegative integer smaller than `2³²` | structure returned by `rng`

Seed for random number generation to obtain reproducible scenarios, specified as a nonnegative integer smaller than 2³² or structure returned by rng that defines the random state. The default value [] means that the generated scenarios will be different every time the generate function is called unless you set the random seed before calling the function or use reproducible sequences such as Sobol or Halton.

Example: 10

Data Types: double | struct

Object Functions

`add`	Add quantity values, doses, or variants to `SimBiology.Scenarios` object
`getEntry`	Get entry contents from `SimBiology.Scenarios` object
`updateEntry`	Update entry contents from `SimBiology.Scenarios` object
`rename`	Rename entry from `SimBiology.Scenarios` object
`remove`	Remove entries from `SimBiology.Scenarios` object
`verify`	Verify `SimBiology.Scenarios` object
`generate`	Generate scenarios from `SimBiology.Scenarios` object and return table
`getNumberScenarios`	Return number of scenarios from `SimBiology.Scenarios` object

Examples

collapse all

Generate Different Simulation Scenarios for Glucose-Insulin Response

This example uses:

Open Live Script

Load the model of glucose-insulin response. For details about the model, see the Background section in Simulate the Glucose-Insulin Response.

sbioloadproject('insulindemo','m1');

The model contains different parameter values and initial conditions that represents different insulin impairments (such as Type 2 diabetes, low insulin sensitivity, and so on) stored in five variants.

variants = getvariant(m1)

variants = 
   SimBiology Variant Array

   Index:  Name:             Active:
   1       Type 2 diabetic   false
   2       Low insulin se... false
   3       High beta cell... false
   4       Low beta cell ... false
   5       High insulin s... false

Suppress an informational warning that is issued during simulations.

warnSettings = warning('off','SimBiology:DimAnalysisNotDone_MatlabFcn_Dimensionless');

Select a dose that represents a single meal of 78 grams of glucose.

singleMeal = sbioselect(m1,'Name','Single Meal');

Create a Scenarios object to represent different initial conditions combined with the dose. That is, create a scenario object where each variant is paired (or combined) with the dose, for a total of five simulation scenarios.

sObj = SimBiology.Scenarios;
add(sObj,'cartesian','variants',variants);
add(sObj,'cartesian','dose',singleMeal)

ans = 
  Scenarios (5 scenarios)

                   Name            Content          Number
                 ________    ___________________    ______

    Entry 1      variants    SimBiology variants      5   
    x Entry 2    dose        SimBiology dose          1   

  See also Expression property.

sObj contains two entries. Use the generate function to combine the entries and generate five scenarios. The function returns a scenarios table, where each row represents a scenario and each column represents an entry of the Scenarios object.

scenariosTbl = generate(sObj)

scenariosTbl=5×2 table
           variants                     dose           
    ______________________    _________________________

    1x1 SimBiology.Variant    1x1 SimBiology.RepeatDose
    1x1 SimBiology.Variant    1x1 SimBiology.RepeatDose
    1x1 SimBiology.Variant    1x1 SimBiology.RepeatDose
    1x1 SimBiology.Variant    1x1 SimBiology.RepeatDose
    1x1 SimBiology.Variant    1x1 SimBiology.RepeatDose

Change the entry name of the first entry.

rename(sObj,1,'Insulin Impairements')

ans = 
  Scenarios (5 scenarios)

                         Name                  Content          Number
                 ____________________    ___________________    ______

    Entry 1      Insulin Impairements    SimBiology variants      5   
    x Entry 2    dose                    SimBiology dose          1   

  See also Expression property.

Create a SimFunction object to simulate the generated scenarios. Use the Scenarios object as the input and specify the plasma glucose and insulin concentrations as responses (outputs of the function to be plotted). Specify [] for the dose input argument since the Scenarios object already has the dosing information.

f = createSimFunction(m1,sObj,{'[Plasma Glu Conc]','[Plasma Ins Conc]'},[])

f = 
SimFunction

Parameters:

               Name                Value         Type                            Units                   
    ___________________________    ______    _____________    ___________________________________________

    {'[Plasma Volume (Glu)]'  }      1.88    {'parameter'}    {'deciliter'                              }
    {'k1'                     }     0.065    {'parameter'}    {'1/minute'                               }
    {'k2'                     }     0.079    {'parameter'}    {'1/minute'                               }
    {'[Plasma Volume (Ins)]'  }      0.05    {'parameter'}    {'liter'                                  }
    {'m1'                     }      0.19    {'parameter'}    {'1/minute'                               }
    {'m2'                     }     0.484    {'parameter'}    {'1/minute'                               }
    {'m4'                     }    0.1936    {'parameter'}    {'1/minute'                               }
    {'m5'                     }    0.0304    {'parameter'}    {'minute/picomole'                        }
    {'m6'                     }    0.6469    {'parameter'}    {'dimensionless'                          }
    {'[Hepatic Extraction]'   }       0.6    {'parameter'}    {'dimensionless'                          }
    {'kmax'                   }    0.0558    {'parameter'}    {'1/minute'                               }
    {'kmin'                   }     0.008    {'parameter'}    {'1/minute'                               }
    {'kabs'                   }    0.0568    {'parameter'}    {'1/minute'                               }
    {'kgri'                   }         0    {'parameter'}    {'1/minute'                               }
    {'f'                      }       0.9    {'parameter'}    {'dimensionless'                          }
    {'a'                      }         0    {'parameter'}    {'1/milligram'                            }
    {'b'                      }      0.82    {'parameter'}    {'dimensionless'                          }
    {'c'                      }         0    {'parameter'}    {'1/milligram'                            }
    {'d'                      }      0.01    {'parameter'}    {'dimensionless'                          }
    {'kp1'                    }       2.7    {'parameter'}    {'milligram/minute'                       }
    {'kp2'                    }    0.0021    {'parameter'}    {'1/minute'                               }
    {'kp3'                    }     0.009    {'parameter'}    {'(milligram/minute)/(picomole/liter)'    }
    {'kp4'                    }    0.0618    {'parameter'}    {'(milligram/minute)/picomole'            }
    {'ki'                     }    0.0079    {'parameter'}    {'1/minute'                               }
    {'[Ins Ind Glu Util]'     }         1    {'parameter'}    {'milligram/minute'                       }
    {'Vm0'                    }    2.5129    {'parameter'}    {'milligram/minute'                       }
    {'Vmx'                    }     0.047    {'parameter'}    {'(milligram/minute)/(picomole/liter)'    }
    {'Km'                     }    225.59    {'parameter'}    {'milligram'                              }
    {'p2U'                    }    0.0331    {'parameter'}    {'1/minute'                               }
    {'K'                      }      2.28    {'parameter'}    {'picomole/(milligram/deciliter)'         }
    {'alpha'                  }      0.05    {'parameter'}    {'1/minute'                               }
    {'beta'                   }      0.11    {'parameter'}    {'(picomole/minute)/(milligram/deciliter)'}
    {'gamma'                  }       0.5    {'parameter'}    {'1/minute'                               }
    {'ke1'                    }    0.0005    {'parameter'}    {'1/minute'                               }
    {'ke2'                    }       339    {'parameter'}    {'milligram'                              }
    {'[Basal Plasma Glu Conc]'}     91.76    {'parameter'}    {'milligram/deciliter'                    }
    {'[Basal Plasma Ins Conc]'}     25.49    {'parameter'}    {'picomole/liter'                         }

Observables: 

            Name                Type                 Units         
    _____________________    ___________    _______________________

    {'[Plasma Glu Conc]'}    {'species'}    {'milligram/deciliter'}
    {'[Plasma Ins Conc]'}    {'species'}    {'picomole/liter'     }

Dosed: 

    TargetName       TargetDimension   
    __________    _____________________

     {'Dose'}     {'Mass (e.g., gram)'}


TimeUnits: hour

Simulate the model for 24 hours and plot the simulation data. The data contains five runs, where each run represents a scenario in the Scenarios object.

sd = f(sObj,24);
sbioplot(sd)

ans = 
  Axes (SbioPlot) with properties:

             XLim: [0 30]
             YLim: [0 450]
           XScale: 'linear'
           YScale: 'linear'
    GridLineStyle: '-'
         Position: [0.0956 0.1100 0.2509 0.8150]
            Units: 'normalized'

  Use GET to show all properties

If you have Statistics and Machine Learning Toolbox™, you can also draw sample values for model quantities from various probability distributions. For instance, suppose that the parameters Vmx and kp3, which are known for the low and high insulin sensitivity, follow the lognormal distribution. You can generate sample values for these parameters from such a distribution, and perform a scan to explore model behavior.

Define the lognormal probability distribution object for Vmx.

pd_Vmx = makedist('lognormal')

pd_Vmx = 
  LognormalDistribution

  Lognormal distribution
       mu = 0
    sigma = 1

By definition, the parameter mu is the mean of logarithmic values. To vary the parameter value around the base (model) value of the parameter, set mu to log(model_value). Set the standard deviation (sigma) to 0.2. For a small sigma value, the mean of a lognormal distribution is approximately equal to log(model_value). For details, see Lognormal Distribution (Statistics and Machine Learning Toolbox).

Vmx = sbioselect(m1,'Name','Vmx');
pd_Vmx.mu = log(Vmx.Value);
pd_Vmx.sigma = 0.2

pd_Vmx = 
  LognormalDistribution

  Lognormal distribution
       mu = -3.05761
    sigma =      0.2

Similarly define the probability distribution for kp3.

pd_kp3 = makedist('lognormal');
kp3 = sbioselect(m1,'Name','kp3');
pd_kp3.mu = log(kp3.Value);
pd_kp3.sigma = 0.2

pd_kp3 = 
  LognormalDistribution

  Lognormal distribution
       mu = -4.71053
    sigma =      0.2

Now define a joint probability distribution to draw sample values for Vmx and kp3, with a rank correlation to specify some correlation between these two parameters. Note that this correlation assumption is for the illustration purposes of this example only and may not be biologically relevant.

First remove the variants entry (entry 1) from sObj.

remove(sObj,1)

ans = 
  Scenarios (1 scenarios)

               Name        Content        Number
               ____    _______________    ______

    Entry 1    dose    SimBiology dose      1   

  See also Expression property.

Add an entry that defines the joint probability distribution with a rank correlation matrix.

add(sObj,'cartesian',["Vmx","kp3"],[pd_Vmx, pd_kp3],'RankCorrelation',[1,0.5;0.5,1])

ans = 
  Scenarios (2 scenarios)

                    Name           Content              Number   
                    ____    ______________________    ___________

    Entry 1         dose    SimBiology dose           1          
    x (Entry 2.1    Vmx     Lognormal distribution    2 (default)
    + Entry 2.2)    kp3     Lognormal distribution    2 (default)

  See also Expression property.

By default, the number of samples to draw from the joint distribution is set to 2. Increase the number of samples.

updateEntry(sObj,2,'Number',50)

ans = 
  Scenarios (50 scenarios)

                    Name           Content            Number
                    ____    ______________________    ______

    Entry 1         dose    SimBiology dose             1   
    x (Entry 2.1    Vmx     Lognormal distribution      50  
    + Entry 2.2)    kp3     Lognormal distribution      50  

  See also Expression property.

Verify that the Scenarios object can be simulated with the model. The verify function throws an error if any entry does not resolve uniquely to an object in the model or the entry contents have inconsistent lengths (sample sizes). The function throws a warning if multiple entries resolve to the same object in the model.

verify(sObj,m1)

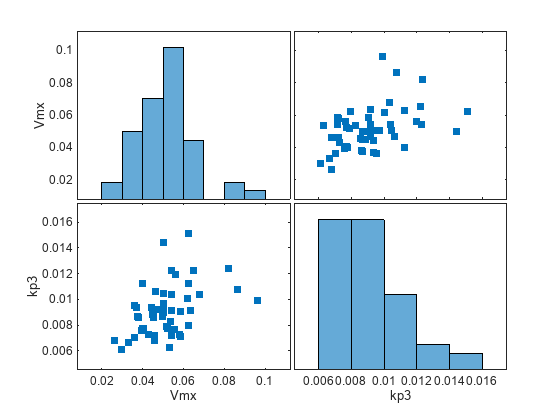
Generate the simulation scenarios. Plot the sample values using plotmatrix. You can see the value of Vmx is varied around its model value 0.047 and that of kp3 around 0.009.

sTbl = generate(sObj);
[s,ax,bigax,h,hax] = plotmatrix([sTbl.Vmx,sTbl.kp3]);
ax(1,1).YLabel.String = "Vmx";
ax(2,1).YLabel.String = "kp3";
ax(2,1).XLabel.String = "Vmx";
ax(2,2).XLabel.String = "kp3";

MATLAB figure

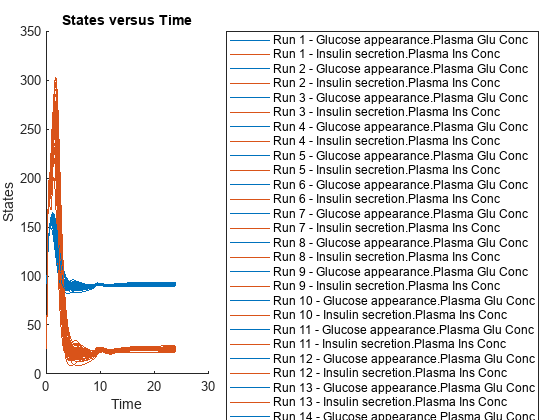
Simulate the scenarios using the same SimFunction you created previously. You do not need to create a new SimFunction object even though the Scenarios object has been updated.

sd2 = f(sObj,24);
sbioplot(sd2);

By default, SimBiology uses the random sampling method. You can change it to the Latin hypercube sampling (or sobol or halton) for a more systematic space-filling approach.

entry2struct = getEntry(sObj,2)

entry2struct = struct with fields:
               Name: {'Vmx'  'kp3'}
            Content: [2x1 prob.LognormalDistribution]
             Number: 50
    RankCorrelation: [2x2 double]
         Covariance: []
     SamplingMethod: 'random'
    SamplingOptions: [0x0 struct]

entry2struct.SamplingMethod = 'lhs'

entry2struct = struct with fields:
               Name: {'Vmx'  'kp3'}
            Content: [2x1 prob.LognormalDistribution]
             Number: 50
    RankCorrelation: [2x2 double]
         Covariance: []
     SamplingMethod: 'lhs'
    SamplingOptions: [0x0 struct]

You can now use the updated structure to modify entry 2.

updateEntry(sObj,2,entry2struct)

ans = 
  Scenarios (50 scenarios)

                    Name           Content            Number
                    ____    ______________________    ______

    Entry 1         dose    SimBiology dose             1   
    x (Entry 2.1    Vmx     Lognormal distribution      50  
    + Entry 2.2)    kp3     Lognormal distribution      50  

  See also Expression property.

Visualize the sample values.

sTbl2 = generate(sObj);
[s,ax,bigax,h,hax] = plotmatrix([sTbl2.Vmx,sTbl2.kp3]);
ax(1,1).YLabel.String = "Vmx";
ax(2,1).YLabel.String = "kp3";
ax(2,1).XLabel.String = "Vmx";
ax(2,2).XLabel.String = "kp3";

MATLAB figure

Simulate the scenarios.

sd3 = f(sObj,24);
sbioplot(sd3);

Restore warning settings.

warning(warnSettings);

More About

expand all

`SimBiology.Scenarios` Terminology

This section annotates the command line display of the SimBiology.Scenarios object and explains the terms shown in the output. Specifically, it explains these terminologies: Scenarios, Entry, Subentry, Name, Content, Number, Expression, inconsistent and Diagnosis.

A consistent Scenarios object has entries that have the correct number of samples so that entries can be combined without error. An example of a consistent Scenarios object is shown next.

An inconsistent Scenarios object has one or more entries with incorrect number of samples. You need to correct these entries before you can use the object for simulation. An example of an inconsistent object is shown next.

The Diagnosis column suggests which entries to fix to have the correct number of samples. Use updateEntry, rename, and remove to edit the entries.

References

[1] Iman, R., and W.J. Conover. 1982. A distribution-free approach to inducing rank correlation among input variables. Communications in Statistics - Simulation and Computation. 11(3):311–334.

Version History

Introduced in R2019b

SimBiology.Scenarios

Description

Creation

Syntax

Description

Input Arguments

`name` — Entry name
character vector | string

`content` — Model quantity values or vector of doses or variants
numeric vector | vector of `RepeatDose` or `ScheduleDose` objects | vector of variant objects

`quantityNames` — Names of model quantities
character vector | string | string vector | cell array of character vectors

`probDist` — Probability distributions
vector of probability distribution objects | character vector | string | string vector | cell array of character vectors

`Number` — Number of samples
`[]` (default) | positive scalar

`RankCorrelation` — Rank correlation matrix
`[]` (default) | numeric matrix

`Mean` — Mean values
numeric vector

`Covariance` — Covariance matrix
`[]` (default) | numeric matrix

`SamplingMethod` — Sampling method
`'random'` (default) | `'lhs'` | `'copula'` | `'sobol'` | `'halton'`

`SamplingOptions` — Options for sampling method
struct

Properties

`Expression` — Combination expression
character vector

`NumberOfEntries` — Number of entries
positive integer

`RandomSeed` — Seed or state for random number generation
`[]` (default) | nonnegative integer smaller than `2³²` | structure returned by `rng`

Object Functions

Examples

Generate Different Simulation Scenarios for Glucose-Insulin Response

More About

`SimBiology.Scenarios` Terminology

References

Version History

See Also

Topics

SimBiology.Scenarios

Description

Creation

Syntax

Description

Input Arguments

name — Entry name character vector | string

content — Model quantity values or vector of doses or variants numeric vector | vector of RepeatDose or ScheduleDose objects | vector of variant objects

quantityNames — Names of model quantities character vector | string | string vector | cell array of character vectors

probDist — Probability distributions vector of probability distribution objects | character vector | string | string vector | cell array of character vectors

Number — Number of samples [] (default) | positive scalar

RankCorrelation — Rank correlation matrix [] (default) | numeric matrix

Mean — Mean values numeric vector

Covariance — Covariance matrix [] (default) | numeric matrix

SamplingMethod — Sampling method 'random' (default) | 'lhs' | 'copula' | 'sobol' | 'halton'

SamplingOptions — Options for sampling method struct

Properties

Expression — Combination expression character vector

NumberOfEntries — Number of entries positive integer

RandomSeed — Seed or state for random number generation [] (default) | nonnegative integer smaller than 232 | structure returned by rng

Object Functions

Examples

Generate Different Simulation Scenarios for Glucose-Insulin Response

More About

SimBiology.Scenarios Terminology

References

Version History

See Also

Topics

`name` — Entry name
character vector | string

`content` — Model quantity values or vector of doses or variants
numeric vector | vector of `RepeatDose` or `ScheduleDose` objects | vector of variant objects

`quantityNames` — Names of model quantities
character vector | string | string vector | cell array of character vectors

`probDist` — Probability distributions
vector of probability distribution objects | character vector | string | string vector | cell array of character vectors

`Number` — Number of samples
`[]` (default) | positive scalar

`RankCorrelation` — Rank correlation matrix
`[]` (default) | numeric matrix

`Mean` — Mean values
numeric vector

`Covariance` — Covariance matrix
`[]` (default) | numeric matrix

`SamplingMethod` — Sampling method
`'random'` (default) | `'lhs'` | `'copula'` | `'sobol'` | `'halton'`

`SamplingOptions` — Options for sampling method
struct

`Expression` — Combination expression
character vector

`NumberOfEntries` — Number of entries
positive integer

`RandomSeed` — Seed or state for random number generation
`[]` (default) | nonnegative integer smaller than `2³²` | structure returned by `rng`

`SimBiology.Scenarios` Terminology