evalRequirement

Create the reference data.

time = (0:0.1:10)';
data = 1-exp(-time);

Create the signal tracking requirement object. Specify the reference signal.

req = sdo.requirements.SignalTracking;
req.ReferenceSignal = timeseries(data,time);

Obtain the test point signal.

sig = timeseries(1-exp(-time/2),time);

Evaluate the signal tracking requirement.

c = evalRequirement(req,sig);

When you estimate parameters for multiple experiments, you repeatedly compare test point and reference signal sets. If you use the same evaluation criteria for all comparisons, you can use the c = evalrequirement(req,sig,ref) syntax. You vary sig and ref, and re-use the requirement object, req. req specifies the estimation error computation options.

Create a reference and test point signal. Then, use a requirement object to evaluate the requirement.

Create the reference signal.

time = (0:0.1:10)';
data = 1-exp(-time);
ref = timeseries(data,time);

Create the signal tracking requirement object. Specify the error computation method.

Specify 'Residuals' as the algorithm for error computation.

req = sdo.requirements.SignalTracking;
req.Method = 'Residuals';

Obtain the test point signal.

sig = timeseries(1-exp(-time/2),time);

Evaluate the signal tracking requirement.

c = evalRequirement(req,sig,ref);

Create a step response requirement.

requirement = sdo.requirements.StepResponseEnvelope;

A requirement is created with the default settling time of 7 seconds.

Specify the signal to be evaluated.

signal = timeseries(1-exp(-(0:10)'));

The signal data extends to 10 seconds.

Evaluate the step response requirement.

evaluation = evalRequirement(requirement,signal)

evaluation = 6×1

   -0.0917
   -0.0099
   -1.0000
   -0.2416
   -0.0092
   -0.0299

The maximum distance of the signal from the step response bounds is returned in evaluation(1:5), followed by the stability value. Negative values indicate that the requirement is satisfied.

The maximum distance from the bounds are returned in the following order:

evaluation does not include the distance of the signal from bounds beyond 1.5*settling time because the signal data does not extend beyond 1.5*settling time.

Create a default requirement object.

Requirement = sdo.requirements.PhasePlaneRegion;

The requirement object specifies the bounding region as a single edge extending from (-1,0) to (-1,1) in the phase plane defined by two signals. Requirement.Type has the default value of '<='. This value implies the area to the left of the edge is out of bounds, where the forward direction is the direction of creation of the edge.

Specify the test signal data as timeseries objects.

signal1 = timeseries(1-exp(-(0:10)'));
signal2 = timeseries(sin((0:10)'));

Evaluate the requirement.

Evaluation = evalRequirement(Requirement,signal1,signal2)

Evaluation = 
-0.2632

A negative value indicates that the requirement is satisfied, and the phase plane trajectory of the two test signal data is in the bounding region.

Create a requirement object to specify a piecewise-linear bound on the phase plane trajectory of two signals. The bound has two edges. The first edge extends from (-4,1) to (2,1). The second edge extends from (2,1) to (2,-4).

Requirement = sdo.requirements.PhasePlaneRegion('BoundX',[-4 2; 2 2],...
    'BoundY',[1 1; 1 -4]);

Specify the bound type as '>='.

Requirement.Type = '>=';

The plot below shows the bounding edges in black. The arrows indicate the direction in which the edges were specified. When you specify the Type property as '>=', the out-of-bound area is always to the right of each edge, where the forward direction is the direction of creation of the edge. As a result, the out-of bound region is the yellow shaded area, and a trajectory point located at (3,3) is in the bounded region.

Evaluate the requirement for the phase plane trajectory point located at (3,3).

Evaluation = evalRequirement(Requirement,[3 3])

Evaluation = 
-0.6389

evalRequirement returns a negative number, indicating the requirement is satisfied.

Now create the requirement by changing the order of specification of the edges.

set(Requirement,'BoundX',[2 2; 2 -4],'BoundY',[-4 1;1 1]);

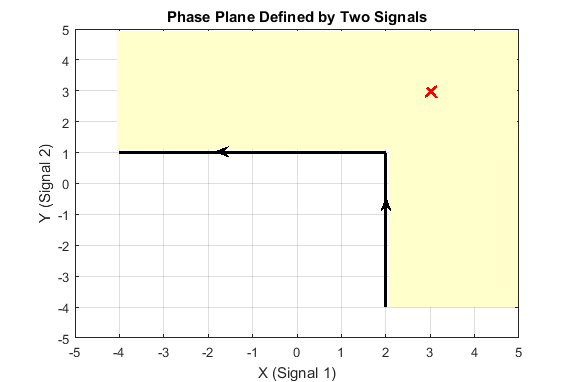
The plot shows that the edges were created in the opposite order. So, even though the requirement type is still '>=', the out-of-bound region, which is always to the right of the edges, is now flipped.

Evaluate the requirement.

Evaluation = evalRequirement(Requirement,[3 3])

Evaluation = 
0.1087

A positive Evaluation value indicates the requirement has been violated. Thus, for the same requirement type, the trajectory point at (3,3) is out of bounds when the edges are defined in the reverse order.

Create a default requirement object.

Requirement = sdo.requirements.PhasePlaneEllipse;

The requirement object specifies the bounding ellipse as an upper bound with center located at [0,0], and no rotation. The x-axis radius of the ellipse is 1 and a y-axis radius is 0.5.

Specify the test signal data as timeseries objects.

signal1 = timeseries(1-exp(-(0:10)'));
signal2 = timeseries(sin((0:10)'));

Evaluate the requirement.

Evaluation = evalRequirement(Requirement,signal1,signal2)

Evaluation = 
0.6997

The default method for requirement evaluation, Requirement.Method is 'Maximum'. Thus, the evalRequirement command computes the signed minimum distance of each point in the phase plane trajectory to the bounding ellipse and then returns the maximum of these distances. A positive value indicates that the at least one point on the phase trajectory lies outside the ellipse and violates the requirement.

To see the signed distance of each of the points on the trajectory to the phase plane ellipse, specify the method for evaluation as 'Residuals'.

Requirement.Method = 'Residuals';

Evaluate the requirement using the new evaluation method.

Evaluation2 = evalRequirement(Requirement,signal1,signal2)

Evaluation2 = 11×1

   -0.5000
    0.4291
    0.5711
   -0.0078
    0.4850
    0.6695
    0.1133
    0.4079
    0.6997
    0.2102
      ⋮

Evaluation2 is the minimum distance of the phase plane trajectory to the bounding ellipse and is a column vector with length equal to the length of the signals.

A negative value indicates that the phase plane trajectory of the two signals at the corresponding time point lies inside the ellipse and satisfies the requirement. A positive value indicates that the phase plane trajectory of the two signals at the corresponding time point lies outside the ellipse and violates the requirement.

You can see that the maximum value in Evaluation2 is the same as Evaluation.

Create a requirement object to match one-dimensional variable data to a linear function.

Requirement = sdo.requirements.FunctionMatching;

Specify the Centers and Scales properties for a one-dimensional variable by using the set command. You specify these properties because their default values are for a two-dimensional variable.

set(Requirement,'Centers',0,'Scales',1);

Specify test data for the one-dimensional variable.

dependentVariable = 0.5+5.*(1:5);

Evaluate the requirement.

evaluation = evalRequirement(Requirement,dependentVariable)

evaluation = 
5.6798e-30

The software computes the linear function using the default independent variable vector [0 1 2 3 4] because you did not specify any independent variable vectors. There is one independent variable because the number of independent variables must equal the number of dimensions of the test data. The size of the independent variable vector equals the size of the test data.

In this example, the processing method has the default value of 'SSE', so evaluation is returned as a scalar value equal to the sum of squares of the errors. evaluation is very close to zero, indicating that the dependentVariable test data almost matches a linear function. Note that machine precision can affect the value of evaluation at such small values.

Create a requirement object, and specify the function to be matched.

Requirement = sdo.requirements.FunctionMatching('Type','purequadratic');

The object specifies that the variables should match a quadratic function with no cross-terms.

Create 2-dimensional test data for the variable.

[X1,X2] = ndgrid((-1:1),(-4:2:4));
dependentVar = X1.^2 + X2.^2;

Specify independent variable vectors to compute the quadratic function.

The number of independent variable vectors must equal the dimensionality of the test data. In addition, the independent variable vectors must be monotonic and have the same size as the test data in the corresponding dimension.

indepVar1 = (-2:0);
indepVar2 = (-6:2:2);

Evaluate if the test data satisfies the requirement.

evaluation = evalRequirement(Requirement,dependentVar,indepVar1,indepVar2)

evaluation = 
6.3950e-29

The evalRequirement command computes an error signal that is the difference between test data and the function of the independent variable vectors. The error signal is further processed to compute evaluation, based on the error processing method specified in Requirement.Method.

In this example, the processing method has the default value of 'SSE', so evaluation is returned as a scalar value equal to the sum of squares of the errors. evaluation is very close to zero, indicating that the dependentVariable test data almost matches a pure quadratic function.

Create test data with cross-terms.

dependentVariable2 = X1.^2 + X2.^2 + X1.*X2;

Evaluate the requirement for the new test data.

evaluation2 = evalRequirement(Requirement,dependentVariable2,indepVar1,indepVar2)

evaluation2 = 
5.3333

The output evaluation2 is greater than evaluation and is substantially different from 0, indicating that dependentVariable2 does not fit a pure-quadratic function as well as dependentVariable fits the function.

Create a requirement object to constrain the gradient magnitude of a one-dimensional variable to 5.5.

Requirement = sdo.requirements.SmoothnessConstraint('GradientBound',5);

Specify test data for the one-dimensional variable. The data is linear with slope equal to 10.

variableData = 10*(1:5);

Evaluate the requirement.

Evaluation = evalRequirement(Requirement,variableData)

Evaluation = 
1

Since you did not specify the spacing between the test data points, the software computes the gradient magnitude assuming that the spacing is 1. Evaluation is positive, indicating that the test data gradient magnitude is greater than the bound, and the requirement is violated.

Create a smoothness constraint requirement object, and specify the gradient bound as 3.

Requirement = sdo.requirements.SmoothnessConstraint;
Requirement.GradientBound = 3;

Specify test data with gradient magnitude value of 2 for a one-dimensional variable. The spacing between the test points is 2.

variableData = 2:2:10;

Evaluate the requirement without specifying the spacing between test points. The software assumes a spacing of 1.

Evaluation = evalRequirement(Requirement,variableData)

Evaluation = 
-0.3333

A negative value indicates that the requirement is satisfied.

Evaluate the requirement using 2 as the spacing between test data points.

Evaluation = evalRequirement(Requirement,variableData,2)

Evaluation = 
-0.6667

The increased spacing reduces the gradient value, and the requirement is still satisfied.

Now evaluate the requirement using 0.5 as the spacing.

Evaluation = evalRequirement(Requirement,variableData,0.5)

Evaluation = 
0.3333

The decreased spacing increases the gradient magnitude value to be above the gradient bound, and the requirement is violated.

Create a requirement object to constrain the gradient magnitude of a 2-dimensional variable to be below 5.5.

Requirement = sdo.requirements.SmoothnessConstraint;

Requirement.GradientBound = 5.5;

Specify 2-dimensional test data for the variable. In this example, generate test data with a gradient magnitude of 5, and use 2 as the spacing between the test data points in each dimension.

[X1,X2] = ndgrid(1:2:20,1:2:10);
variableData = 3*X1+4*X2;

The gradient of the test data in the two dimensions is 3 and 4. Therefore, the gradient magnitude of the test data is 5 ( = $$\sqrt{3^2+4^2}$$).

Specify the coordinates of the test data in each dimension.

indepVar1 = [1:2:20];
indepVar2 = [1:2:10];

The specified coordinates indicate that the spacing between the test data points in both dimensions is 2.

Evaluate if the test data satisfies the requirement.

Evaluation = evalRequirement(Requirement,variableData,indepVar1,indepVar2)

Evaluation = 
-0.0909

Evaluation is a negative number, indicating that the requirement is satisfied, and the test data gradient magnitude is below the specified bound.

Create a requirement object with default properties.

Requirement = sdo.requirements.MonotonicVariable;

Specify the requirement type for a 1-dimensional variable as monotonically decreasing.

Requirement.Type = {'>'};

Specify test data for a 1-dimensional variable.

Data = [20; 15; 25; 26];

Evaluate if the test data satisfies the requirement.

Evaluation = evalRequirement(Requirement,Data)

Evaluation = 
10

Since Evaluation is a positive number, it shows that the requirement is violated. To understand the magnitude of Evaluation, consider the elements of the test data. While 20>15 satisfies the '>' requirement, 15<25 and 25<26 violate the requirement, resulting in a positive Evaluation value. Because the elements 15 and 25 violate the requirement the most, the magnitude of Evaluation is 10, the difference between these elements.

Create a requirement object, and specify the monotonicity for a 2-dimensional variable.

Requirement = sdo.requirements.MonotonicVariable('Type',{'<','>'});

The object requires the elements in the first dimension of the variable to be monotonically increasing and the elements in the second dimension to be monotonically decreasing.

Specify 2-dimensional test data for the variable.

Data = [10 5; 20 24;30 33];

Evaluate if the test data satisfies the requirement.

Evaluation = evalRequirement(Requirement,Data)

Evaluation = 2×1

    -9
     4

Evaluation is column vector with size corresponding to the dimensions of the test data.

To understand the magnitude of Evaluation, consider the elements of the test data along each dimension. For the first dimension of the test data, going down the rows, the software checks the '<' requirement. Since 10<20<30 and 5<24<33 both satisfy the requirement, Evaluation(1) is a negative number. Because 24<33 comes closest to violating the requirement, the magnitude of Evaluation for this dimension is 9, the difference between these two elements.

For the second dimension of the test data, going across the columns, the software checks, the '>' requirement. While 10>5 satisfies the requirement, 20<24 and 30<33 do not satisfy the requirement. This results in Evaluation(2) being a positive number, indicating that the requirement is not satisfied. Because the elements 20 and 24 violate the requirement the most, the magnitude of Evaluation(2) is 4, the difference between these elements.

Create a requirement object, and specify that the elements of the first variable should be greater than elements of the second variable.

Requirement = sdo.requirements.RelationalConstraint('Type','>');

Specify test data for the two variables. The test data for both variables must be the same size.

varData1 = [20 -3 7];
varData2 = [20 -1 6];

Evaluate whether the test data satisfy the requirement.

Evaluation = evalRequirement(Requirement,varData1,varData2)

Evaluation = 1×3

    0.0000    2.0000   -1.0000

Evaluation is always the same size as the test data. When the relation type is specified as '>', if the requirement is satisfied, evalRequirement returns a negative number with magnitude equal to the absolute value of difference between the two elements. If the requirement is violated, Evaluation is a positive number with magnitude equal to the absolute value of the difference between the two elements, or 0 if the elements are equal.

The first elements of the two variables are equal, so the requirement is violated and Evaluation(1) is 0, the difference between the elements.

The second elements, -3 and -1, violate the requirement, resulting in a positive Evaluation(2) with value = abs(-3-(-1))= 2.

The third elements, 7 and 6, satisfy the requirement, resulting in a negative Evaluation(3) with value = -abs(7-6)= -1.

Create a requirement object, and specify that the elements of two variables should be equal to each other.

Requirement = sdo.requirements.RelationalConstraint('Type','==');

Specify test data for the two variables.

varData1 = [20 15];
varData2 = [20 55];

Evaluate whether the test data satisfies the requirement.

Evaluation = evalRequirement(Requirement,varData1,varData2)

Evaluation = 1×2

     0   -40

Evaluation is the same size as the test data. When the relation type is specified as '==', if the requirement is satisfied, evalRequirement returns 0, the difference between the elements. If the requirement is violated, Evaluation is a non-zero number equal to the difference between the two elements.

The first elements of the two variables are equal, so the requirement is satisfied and Evaluation(1) is 0.

The second elements, 15 and 55, violate the requirement, resulting in a non-zero Evaluation(2).

You can evaluate frequency-domain requirements for an LTI dynamic system model.

 req = sdo.requirements.BodeMagnitude;
 sys = tf(1,[1 2 2 1]);
 c = evalRequirement(req,sys);

 req = sdo.requirements.BodeMagnitude;
 

 c = evalRequirement(req,sys);

 req2 = sdo.requirements.PZDampingRatio;
 c2 = evalRequirement(req2,sys);