kfoldMargin

Load the NLP data set.

load nlpdata

X is a sparse matrix of predictor data, and Y is a categorical vector of class labels.

For simplicity, use the label 'others' for all observations in Y that are not 'simulink', 'dsp', or 'comm'.

Y(~(ismember(Y,{'simulink','dsp','comm'}))) = 'others';

Cross-validate a multiclass, linear classification model.

rng(1); % For reproducibility 
CVMdl = fitcecoc(X,Y,'Learner','linear','CrossVal','on');

CVMdl is a ClassificationPartitionedLinearECOC model. By default, the software implements 10-fold cross validation. You can alter the number of folds using the 'KFold' name-value pair argument.

Estimate the k-fold margins.

m = kfoldMargin(CVMdl);
size(m)

ans = 1×2

       31572           1

m is a 31572-by-1 vector. m(j) is the average of the out-of-fold margins for observation j.

Plot the k-fold margins using box plots.

figure;
boxplot(m);
h = gca;
h.YLim = [-5 5];
title('Distribution of Cross-Validated Margins')

One way to perform feature selection is to compare k-fold margins from multiple models. Based solely on this criterion, the classifier with the larger margins is the better classifier.

Load the NLP data set. Preprocess the data as in Estimate k-Fold Cross-Validation Margins, and orient the predictor data so that observations correspond to columns.

load nlpdata
Y(~(ismember(Y,{'simulink','dsp','comm'}))) = 'others';
X = X';

Create these two data sets:

rng(1); % For reproducibility
p = size(X,1); % Number of predictors
halfPredIdx = randsample(p,ceil(0.5*p));
fullX = X;
partX = X(halfPredIdx,:);

Create a linear classification model template that specifies optimizing the objective function using SpaRSA.

t = templateLinear('Solver','sparsa');

Cross-validate two ECOC models composed of binary, linear classification models: one that uses the all of the predictors and one that uses half of the predictors. Indicate that observations correspond to columns.

CVMdl = fitcecoc(fullX,Y,'Learners',t,'CrossVal','on',...
    'ObservationsIn','columns');
PCVMdl = fitcecoc(partX,Y,'Learners',t,'CrossVal','on',...
    'ObservationsIn','columns');

CVMdl and PCVMdl are ClassificationPartitionedLinearECOC models.

Estimate the k-fold margins for each classifier. Plot the distribution of the k-fold margins sets using box plots.

fullMargins = kfoldMargin(CVMdl);
partMargins = kfoldMargin(PCVMdl);

figure;
boxplot([fullMargins partMargins],'Labels',...
    {'All Predictors','Half of the Predictors'});
h = gca;
h.YLim = [-1 1];
title('Distribution of Cross-Validated Margins')

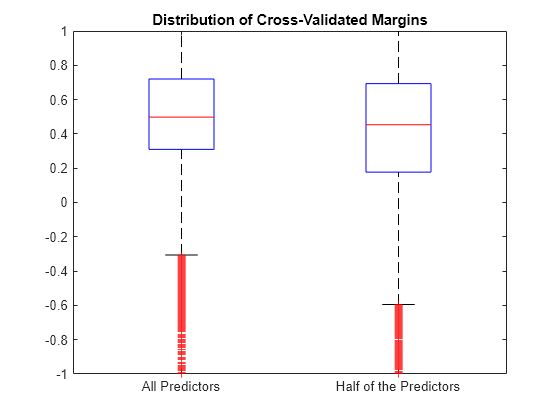
The distributions of the k-fold margins of the two classifiers are similar.

To determine a good lasso-penalty strength for a linear classification model that uses a logistic regression learner, compare distributions of k-fold margins.

Load the NLP data set. Preprocess the data as in Feature Selection Using k-fold Margins.

load nlpdata
Y(~(ismember(Y,{'simulink','dsp','comm'}))) = 'others';
X = X';

Create a set of 11 logarithmically-spaced regularization strengths from $$10^{-8}$$ through $$10^1$$.

Lambda = logspace(-8,1,11);

Create a linear classification model template that specifies using logistic regression with a lasso penalty, using each of the regularization strengths, optimizing the objective function using SpaRSA, and reducing the tolerance on the gradient of the objective function to 1e-8.

t = templateLinear('Learner','logistic','Solver','sparsa',...
    'Regularization','lasso','Lambda',Lambda,'GradientTolerance',1e-8);

Cross-validate an ECOC model composed of binary, linear classification models using 5-fold cross-validation and that

rng(10); % For reproducibility
CVMdl = fitcecoc(X,Y,'Learners',t,'ObservationsIn','columns','KFold',5)

CVMdl = 
  ClassificationPartitionedLinearECOC
    CrossValidatedModel: 'LinearECOC'
           ResponseName: 'Y'
        NumObservations: 31572
                  KFold: 5
              Partition: [1x1 cvpartition]
             ClassNames: [comm    dsp    simulink    others]
         ScoreTransform: 'none'

CVMdl is a ClassificationPartitionedLinearECOC model.

Estimate the k-fold margins for each regularization strength. The scores for logistic regression are in [0,1]. Apply the quadratic binary loss.

m = kfoldMargin(CVMdl,'BinaryLoss','quadratic');
size(m)

ans = 1×2

       31572          11

m is a 31572-by-11 matrix of cross-validated margins for each observation. The columns correspond to the regularization strengths.

Plot the k-fold margins for each regularization strength.

figure;
boxplot(m)
ylabel('Cross-validated margins')
xlabel('Lambda indices')

Several values of Lambda yield similarly high margin distribution centers with low spreads. Higher values of Lambda lead to predictor variable sparsity, which is a good quality of a classifier.

Choose the regularization strength that occurs just before the margin distribution center starts decreasing and spread starts increasing.

LambdaFinal = Lambda(5);

Train an ECOC model composed of linear classification model using the entire data set and specify the regularization strength LambdaFinal.

t = templateLinear('Learner','logistic','Solver','sparsa',...
    'Regularization','lasso','Lambda',Lambda(5),'GradientTolerance',1e-8);
MdlFinal = fitcecoc(X,Y,'Learners',t,'ObservationsIn','columns');

To estimate labels for new observations, pass MdlFinal and the new data to predict.