高斯混合分布的概率密度函数
说明
示例
创建一个 gmdistribution 对象并计算其 pdf 值。
定义一个二成分二元高斯混合分布的分布参数（均值和协方差）。
mu = [1 2;-3 -5];
sigma = [1 1]; % shared diagonal covariance matrix使用 gmdistribution 函数创建一个 gmdistribution 对象。默认情况下，该函数会创建一个等比例混合。
gm = gmdistribution(mu,sigma)
gm = Gaussian mixture distribution with 2 components in 2 dimensions Component 1: Mixing proportion: 0.500000 Mean: 1 2 Component 2: Mixing proportion: 0.500000 Mean: -3 -5
计算 gm 的 pdf 值。
X = [0 0;1 2;3 3;5 3]; pdf(gm,X)
ans = 4×1
0.0065
0.0796
0.0065
0.0000
创建一个 gmdistribution 对象并对绘制其 pdf。
定义两个二元高斯混合成分的分布参数（均值、协方差和混合比例）。
p = [0.4 0.6]; % Mixing proportions mu = [1 2;-3 -5]; % Means sigma = cat(3,[2 .5],[1 1]) % Covariances 1-by-2-by-2 array
sigma =
sigma(:,:,1) =
2.0000 0.5000
sigma(:,:,2) =
1 1
cat 函数沿第三个数组维度串联协方差。定义的协方差矩阵是对角矩阵。sigma(1,:,i) 包含成分 i 的协方差矩阵的对角线元素。
使用 gmdistribution 函数创建一个 gmdistribution 对象。
gm = gmdistribution(mu,sigma)
gm = Gaussian mixture distribution with 2 components in 2 dimensions Component 1: Mixing proportion: 0.500000 Mean: 1 2 Component 2: Mixing proportion: 0.500000 Mean: -3 -5
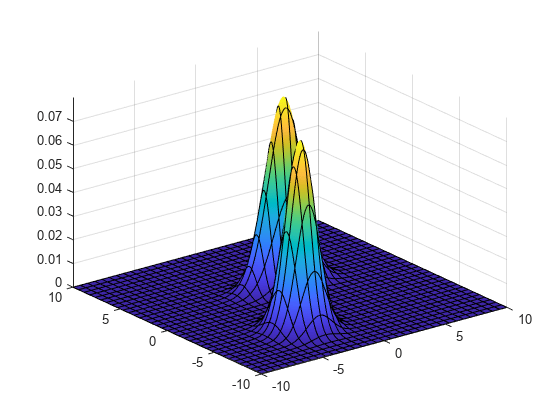
使用 fsurf 绘制高斯混合分布的 pdf。
gmPDF = @(x,y) arrayfun(@(x0,y0) pdf(gm,[x0 y0]),x,y); fsurf(gmPDF,[-10 10])
输入参数
输出参量
版本历史记录
在 R2007b 中推出
