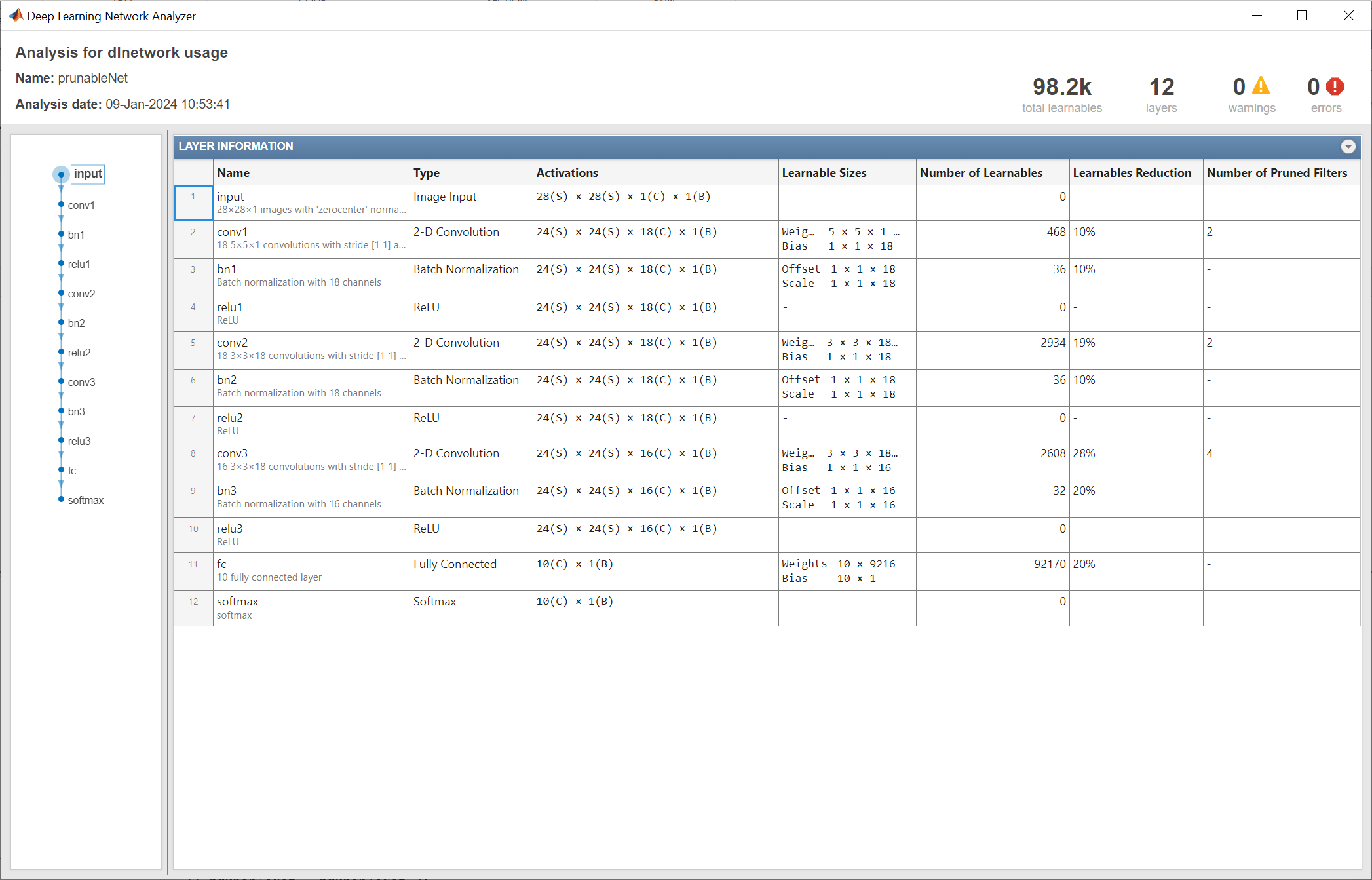
taylorPrunableNetwork

Neural network suitable for compression using Taylor pruning

Since R2022a

Description

A TaylorPrunableNetwork object enables support for compression of neural networks using Taylor pruning.

Pruning a neural network means removing the least important parameters to reduce the size of the network while preserving the quality of its predictions as much as possible.

Find the least important parameters in a pretrained network by iterating over these steps:

Determine the importance score of the prunable parameters and remove the least important parameters.
Retrain the updated network for several iterations.

Removing the least important parameters in each iteration of the pruning loop is computationally expensive. Use a TaylorPrunableNetwork object to simulate pruning by applying a pruning mask. Use the object functions to update the mask during the pruning loop. Finally, update the network architecture by converting the network back to a dlnetwork object.

For an example of the full pruning workflow, see Prune Image Classification Network Using Taylor Scores.

Creation

Syntax

prunableNet = taylorPrunableNetwork(net)

Description

prunableNet = taylorPrunableNetwork(net) first checks whether the neural network net supports pruning. If so, the function converts net into a TaylorPrunableNetwork object.

example

Input Arguments

expand all

`net` — Neural network architecture
`dlnetwork` object | layer array

Neural network architecture, specified as a dlnetwork object or a layer array.

The Taylor pruning algorithm prunes filters from convolution1dLayer (since R2024b) and convolution2dLayer objects. Pruning convolutional filters can also reduce the number of learnable parameters in downstream layers, for example:

batchNormalizationLayer
fullyConnectedLayer
groupedConvolution2dLayer
transposedConv2dLayer
transposedConv1dLayer (since R2024b)
layerNormalizationLayer (since R2024b)

For some network architectures, data dependency between the layers that support pruning and other layers in the network can prevent pruning of filters. These are some example architectures that exhibit this behavior:

Your network has a convolution2dLayer, a groupNormalizationLayer and another convolution2dLayer connected in sequence. The presence of the group normalization layer prevents pruning of filters of the first convolution layer, because doing so changes the shape of the input channels of the group normalization layer.
Your network has a convolution2dLayer connected in sequence to a softmaxLayer at the end of the network. This architecture prevents pruning of filters of the convolution layer because doing so changes the output size of the network.

Use the Deep Network Designer app to analyze the impact of your network architecture on pruning. Open your network in Deep Network Designer. Then, click Analyze for compression.

Properties

expand all

`Learnables` — Network learnable parameters
table

Network learnable parameters, specified as a table with three columns:

Layer — Layer name, specified as a string scalar.
Parameter — Parameter name, specified as a string scalar.
Value — Value of parameter, specified as a dlarray object.

The network learnable parameters contain the features learned by the network. For example, the weights of convolution and fully connected layers.

The learnable parameter values can be complex-valued (since R2024a).

Data Types: table

`State` — Network state
table

Network state, specified as a table.

The network state is a table with three columns:

Layer – Layer name, specified as a string scalar.
Parameter – State parameter name, specified as a string scalar.
Value – Value of state parameter, specified as a dlarray object.

Layer states contain information calculated during the layer operation to be retained for use in subsequent forward passes of the layer. For example, the cell state and hidden state of LSTM layers, or running statistics in batch normalization layers.

For recurrent layers, such as LSTM layers, with the HasStateInputs property set to 1 (true), the state table does not contain entries for the states of that layer.

During training or inference, you can update the network state using the output of the forward and predict functions.

The state values can be complex-valued (since R2024a).

Data Types: table

`InputNames` — Names of network inputs
cell array of character vectors

This property is read-only.

Names of the network inputs, specified as a cell array of character vectors.

Network inputs are the input layers and the unconnected inputs of layers.

For input layers and layers with a single input, the input name is the name of the layer. For layers with multiple inputs, the input name is "layerName/inputName", where layerName is the name of the layer and inputName is the name of the layer input.

For networks with multiple inputs, training and prediction functions use this property to determine the order of the inputs. For example, for in-memory inputs X1,...,XM to the predict function, the order of the inputs must match the order of the corresponding inputs in the InputNames property of the network.

Data Types: cell

`OutputNames` — Names of network outputs
cell array of character vectors

Names of the network outputs, specified as a cell array of character vectors.

For layers with a single output, the output name is the name of the layer. For layers with multiple outputs, the output name is "layerName/outputName", where layerName is the name of the layer and outputName is the name of the layer output.

If you do not specify the output names, then when you create the network, the software sets the OutputNames property to the layers with unconnected outputs.

For networks with multiple outputs, training and prediction functions use this property to determine the order of the outputs. For example, the outputs Y1,...,YN of the predict function correspond to the outputs specified by the OutputNames property of the network.

Data Types: cell

`NumPrunables` — Number of convolution layer filters that are suitable for pruning
nonnegative integer

Number of convolution layer filters in the network that are suitable for compression using Taylor pruning, specified as a nonnegative integer.

Object Functions

`forward`	Compute deep learning network output for training
`predict`	Compute deep learning network output for inference
`updatePrunables`	Remove filters from prunable layers based on importance scores
`updateScore`	Compute and accumulate Taylor-based importance scores for pruning
`dlnetwork`	Deep learning neural network

Examples

collapse all

Create Taylor Prunable Network

This example uses:

Open Live Script

Load a pretrained SqueezeNet neural network.

net = imagePretrainedNetwork;

Convert the network into a taylorPrunableNetwork object.

prunableNet = taylorPrunableNetwork(net)

prunableNet = 
  TaylorPrunableNetwork with properties:

      Learnables: [52x3 table]
           State: [0x3 table]
      InputNames: {'data'}
     OutputNames: {'prob_flatten'}
    NumPrunables: 2368

Analyze Taylor Prunable Network

This example uses:

Open Live Script

Load a trained and pruned taylorPrunableNetwork object.

load("prunedDigitsCustom.mat");

Analyze the network. analyzeNetwork displays an interactive plot of the network architecture and a table containing information about the network layers. The table shows the number of pruned convolutional filters. The table also shows the percentage decrease in the number of learnables for each layer. This includes the three convolutional layers, but also downstream effects in other layers that do not have pruned filters.

info = analyzeNetwork(prunableNet);

Programmatically view the layer information table.

info.LayerInfo

ans=12×9 table
      Name               Type             ActivationSizes    ActivationFormats                     LearnableSizes                     NumLearnables                       StateSizes                       LearnablesReduction    NumPrunedFilters
    _________    _____________________    _______________    _________________    ________________________________________________    _____________    ________________________________________________    ___________________    ________________

    "input"      "Image Input"            {[ 28 28 1 1]}        {["SSCB"]}        {[dictionary (string --> cell) with no entries]}            0        {[dictionary (string --> cell) with no entries]}                0                 0        
    "conv1"      "2-D Convolution"        {[24 24 18 1]}        {["SSCB"]}        {[dictionary (string --> cell) with 2 entries ]}          468        {[dictionary (string --> cell) with no entries]}              0.1                 2        
    "bn1"        "Batch Normalization"    {[24 24 18 1]}        {["SSCB"]}        {[dictionary (string --> cell) with 2 entries ]}           36        {[dictionary (string --> cell) with 2 entries ]}              0.1                 0        
    "relu1"      "ReLU"                   {[24 24 18 1]}        {["SSCB"]}        {[dictionary (string --> cell) with no entries]}            0        {[dictionary (string --> cell) with no entries]}                0                 0        
    "conv2"      "2-D Convolution"        {[24 24 18 1]}        {["SSCB"]}        {[dictionary (string --> cell) with 2 entries ]}         2934        {[dictionary (string --> cell) with no entries]}           0.1895                 2        
    "bn2"        "Batch Normalization"    {[24 24 18 1]}        {["SSCB"]}        {[dictionary (string --> cell) with 2 entries ]}           36        {[dictionary (string --> cell) with 2 entries ]}              0.1                 0        
    "relu2"      "ReLU"                   {[24 24 18 1]}        {["SSCB"]}        {[dictionary (string --> cell) with no entries]}            0        {[dictionary (string --> cell) with no entries]}                0                 0        
    "conv3"      "2-D Convolution"        {[24 24 16 1]}        {["SSCB"]}        {[dictionary (string --> cell) with 2 entries ]}         2608        {[dictionary (string --> cell) with no entries]}          0.27956                 4        
    "bn3"        "Batch Normalization"    {[24 24 16 1]}        {["SSCB"]}        {[dictionary (string --> cell) with 2 entries ]}           32        {[dictionary (string --> cell) with 2 entries ]}              0.2                 0        
    "relu3"      "ReLU"                   {[24 24 16 1]}        {["SSCB"]}        {[dictionary (string --> cell) with no entries]}            0        {[dictionary (string --> cell) with no entries]}                0                 0        
    "fc"         "Fully Connected"        {[      10 1]}        {["CB"  ]}        {[dictionary (string --> cell) with 2 entries ]}        92170        {[dictionary (string --> cell) with no entries]}          0.19998                 0        
    "softmax"    "Softmax"                {[      10 1]}        {["CB"  ]}        {[dictionary (string --> cell) with no entries]}            0        {[dictionary (string --> cell) with no entries]}                0                 0

Algorithms

Pruning a neural network means removing the least important parameters to reduce the size of the network while preserving the quality of its predictions.

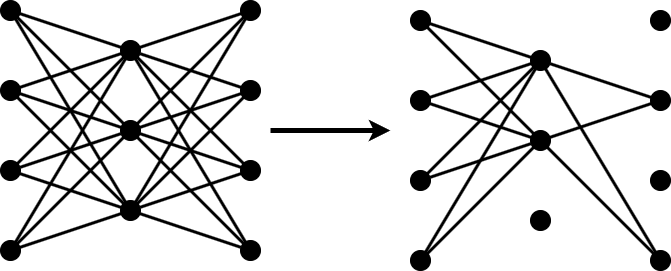
You can measure the importance of a set of parameters by the change in loss after removal of the parameters from the network. If the loss changes significantly, then the parameters are important. If the loss does not change significantly, then the parameters are not important and can be pruned.

When you have a large number of parameters in your network, you cannot calculate the change in loss for all possible combinations of parameters. Instead, apply an iterative workflow.

Use an approximation to find and remove the least important parameter, or the n least important parameters.
Fine-tune the new, smaller network by retraining it for a couple of iterations.
Repeat steps 1 and 2 until you reach your desired memory reduction or until you cannot recover the accuracy drop via fine-tuning.

One option for the approximation in step 1 is to calculate the Taylor expansion of the loss as a function of the individual network parameters. This method is called Taylor pruning.

For some types of layers, including convolutional layers, removing a parameter is equivalent to setting it to zero. In this case, the change in loss resulting from pruning a parameter θ can be expressed as follows.

$| Δ loss (X, θ) | = | loss (X, θ = 0) - loss (X, θ) | .$

Here, X is the training data of your network.

Calculate the Taylor expansion of the loss as a function of the parameter θ to first order.

$loss (X, θ) = loss (X, θ = 0) + \frac{δ loss}{δ θ} θ .$

Then, you can express the change of loss as a function of the gradient of the loss with respect to the parameter θ.

$| Δ loss (X, θ) | = | \frac{δ loss}{δ θ} θ | .$

References

[1] Molchanov, Pavlo, Stephen Tyree, Tero Karras, Timo Aila, and Jan Kautz. "Pruning Convolutional Neural Networks for Resource Efficient Inference." Preprint, submitted June 8, 2017. https://arxiv.org/abs/1611.06440.

Version History

Introduced in R2022a

expand all

R2024b: `taylorPrunableNetwork` supports pruning 1-D convolution layers

The taylorPrunableNetwork function now supports pruning convolution1dLayer layers. Pruning convolutional filters can now also reduce the number of learnable parameters in downstream transposedConv1dLayer and layerNormalizationLayer layers.

R2024a: Complex-valued learnables and state

The values in the Learnables and State properties can be complex-valued.

R2024a: `LayerGraph` objects are not recommended

Starting in R2024a, LayerGraph objects are not recommended. Use dlnetwork objects instead. This recommendation means that LayerGraph input is not recommended to the taylorPrunableNetwork function.

Most functions that support LayerGraph objects also support dlnetwork objects. This table shows some typical usages of LayerGraph objects and how to update your code to use dlnetwork object functions instead.

Not Recommended	Recommended
`lgraph = layerGraph;`	`net = dlnetwork;`
`lgraph = layerGraph(layers);`	`net = dlnetwork(layers,Initialize=false);`
`lgraph = layerGraph(net);`	`net = dag2dlnetwork(net);`
`lgraph = addLayers(lgraph,layers);`	`net = addLayers(net,layers);`
`lgraph = removeLayers(lgraph,layerNames);`	`net = removeLayers(net,layerNames);`
`lgraph = replaceLayer(lgraph,layerName,layers);`	`net = replaceLayer(net,layerName,layers);`
`lgraph = connectLayers(lgraph,s,d);`	`net = connectLayers(net,s,d);`
`lgraph = disconnectLayers(lgraph,s,d);`	`net = disconnectLayers(net,s,d);`
`plot(lgraph);`	`plot(net);`

To train a neural network specified as a dlnetwork object, use the trainnet function.

taylorPrunableNetwork

Description

Creation

Syntax

Description

Input Arguments

`net` — Neural network architecture
`dlnetwork` object | layer array

Properties

`Learnables` — Network learnable parameters
table

`State` — Network state
table

`InputNames` — Names of network inputs
cell array of character vectors

`OutputNames` — Names of network outputs
cell array of character vectors

`NumPrunables` — Number of convolution layer filters that are suitable for pruning
nonnegative integer

Object Functions

Examples

Create Taylor Prunable Network

Analyze Taylor Prunable Network

Algorithms

References

Version History

R2024b: `taylorPrunableNetwork` supports pruning 1-D convolution layers

R2024a: Complex-valued learnables and state

R2024a: `LayerGraph` objects are not recommended

See Also

Topics

taylorPrunableNetwork

Description

Creation

Syntax

Description

Input Arguments

net — Neural network architecture dlnetwork object | layer array

Properties

Learnables — Network learnable parameters table

State — Network state table

InputNames — Names of network inputs cell array of character vectors

OutputNames — Names of network outputs cell array of character vectors

NumPrunables — Number of convolution layer filters that are suitable for pruning nonnegative integer

Object Functions

Examples

Create Taylor Prunable Network

Analyze Taylor Prunable Network

Algorithms

References

Version History

R2024b: taylorPrunableNetwork supports pruning 1-D convolution layers

R2024a: Complex-valued learnables and state

R2024a: LayerGraph objects are not recommended

See Also

Topics

`net` — Neural network architecture
`dlnetwork` object | layer array

`Learnables` — Network learnable parameters
table

`State` — Network state
table

`InputNames` — Names of network inputs
cell array of character vectors

`OutputNames` — Names of network outputs
cell array of character vectors

`NumPrunables` — Number of convolution layer filters that are suitable for pruning
nonnegative integer

R2024b: `taylorPrunableNetwork` supports pruning 1-D convolution layers

R2024a: `LayerGraph` objects are not recommended